
Wir werden im folgenden einige Konstruktionen die wir bereits aus verschiedenen Hochsprachen kennen auf das einfach getypte λ-Kalkül übertragen.

Wir erweitern unsere abstrakte Syntax um die Terme error und
try t onError t. Der Term error wird dabei nicht
den Werten zugeordnet. Die Auswertung einer Funktionsapplikation würde normalerweise
stecken bleiben sobald es sich bei einem der Terme um error handelt.
Dies wird durch die Auswertungsregeln (1) und (2) vermieden. Auch hier wird
die Auswertungsreihenfolge wieder gesteuert, indem Regel (2) als ersten Term
einen Wert fordet. Der Term error wird immer weiter
hochgereicht, bis entweder der gesamte Term (das Programm) zu error
ausgewertet wird, oder der Fehler mit Regel (4) aufgefangen wird.
Betrachten wir als Beispiel die Auswertung des Terms try (λx:Unit.x) error onError unit:
|
Nach der Typregel (1) kann der Term error jeden beliebigen Typ annehmen.
So hat error im Term (λx:Unit.x) error den Typ
Unit wohingegen error im Term
(λx:Unit→Unit.x unit) error
den Typ Unit→Unit hat. Die Typregel (2) fordert, dass der try-Term
den gleichen Typ wie der onError-Term hat.
Betrachten wir nun die Eigenschaften dieses Kalküls:
Werte sind in Terme in Normalform:
Gilt wie bisher.
Jeder Term in Normalform ist ein Wert oder error:
Gilt mit dem oben gemachten Zusatz.
Die Auswertung (→) erfolgt deterministisch:
Gilt wie bisher.
Jeder wohlgetypte Term hat eine Normalform:
Gilt wie bisher.
Progress (Fortschritt):
Wohlgetypte Terme sind entweder in Normalform (d.h. sie sind
Werte oder error) oder sie können noch einen Auswertungsschritt durchlaufen
(d.h. es gibt ein t' so dass t→t').
Preservation (Typerhaltung):
Gilt wie bisher.
Hinweise zur Implementierung:
Das Typaxiom(1) Γ |- error:T ist schwierig zu implementieren.
Bisher konnter wir jedem Term eindeutig einen Typ zuordnen, nun müßen wir sagen: Dieser Term
hat jeden beliebigen Typ. Eine Lösung besteht darin error in allen anderen Typregeln
explizit zu berücksichtigen. Eleganter kann das Problem gelöst werden, wenn unser
Typsystem polymorphe Typen kennt. Dann kann man error den Typ
∀X.X geben.
Hinweis: Im folgenden werden wir häufig auf Basistypen wie String, Bool, Int
oder Float zurückgreifen, die wir bisher nicht formal definiert haben.
Wir benutzen diese Typen lediglich um Beispiele anschaulicher zu machen. Zur formalen
Korrektheit könnte man beispielsweise alle Vorkommen von Bool durch
Unit, von true und false durch unit,
von String durch Unit→Unit und
von "Stringliteral" durch (λx:Unit.x) ersetzen.
Wir wollen Daten unterschiedlichen Typs zu Strukturen zusammenfassen. Diese Strukturen
nennen wir (wie zum Beispiel in Pascal) Records. Ein Record besteht aus 0 bis n Feldern.
Jedes Feld eines Records hat einen Namen und einen Typ. Es gibt Record-Terme
wie beispielsweise {strasse="Feldstraße 143",ort="22880 Wedel"}
und Record-Typen wie {strasse:String, ort:String}. Einzelne
Felder eines Records können selektiert werden r.strasse.
Das leere Records bezeichnen wir mit {}. {} ist ein Wert. Der Typ von {} ist {}.
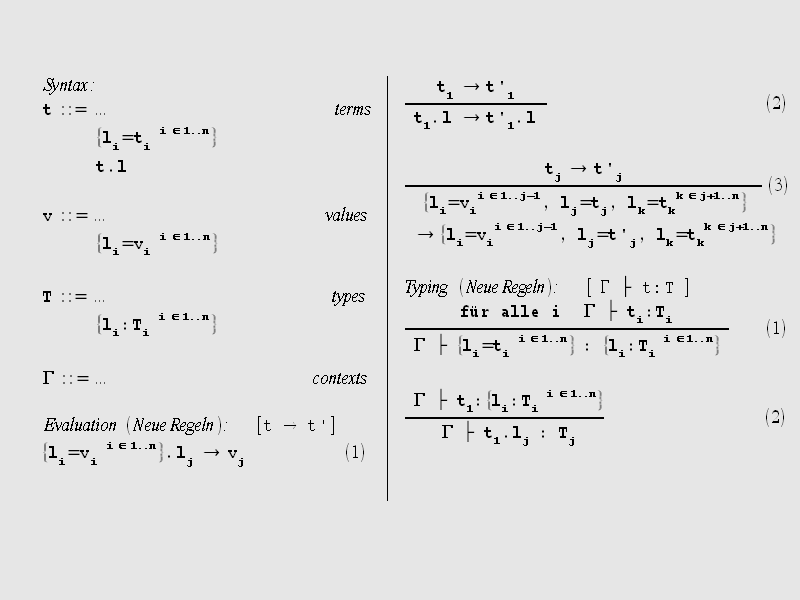
Die operationale Semantik gibt wieder eine Auswertungsreihenfolge für Records vor: Bei der Elementselektion müssen alle Elemente des Records ausgewertet sein. Die Elemente eines Records werden von links nach rechts ausgewertet. Bei Record-Termen ergibt sich der Typ des Record-Terms aus den Namen der Felder und den Typen der den Feldern zugeordneten Terme (Typregel 1). Der Typ der Feldselektion ist der Typ des Feldes mit dem Namen der Feldselektion (Typregel 2).
Betrachten wir den Term
Records können auch geschachtelt auftreten so hat
Übung: Nach den bisherigen Regeln funktioniert unser Exception Handling
nicht mit den hier beschriebenen Records zusammen. Es kann passieren, dass
Exceptions in Records steckenbleiben:
Betrachten wir unsere
In einem ersten Schritt haben wir eine neue Typregel eingeführt, die folgendes besagt:
Lässt sich im Kontext Γ der Typ S für dem Term t ableiten, dann darf
für den Term t auch ein Typ T eingesetzt werden, solange wie T mindestens so allgemein
wie S ist. Statt T ist mindestens so allgemein wie S wird gesagt S ist ein
Subtyp von T. Kurz S<:T.
Nun wollen wir die Subtyp-Relation S<:T näher beschreiben. Sie ist reflexiv (Regel 1),
transitiv (Regel 2) und es gibt einen allgemeinsten Typ
In unserem Beispiel ist die Regel (5) ausreichend um den folgenden Ausdruck wohlgetypt
werden zu lassen.
Kovarianz, Contravarianz und Invarianz
Interessanter wird es, wenn wir die Regeln (4) und (6) betrachten. Wir werden dazu die Begriffe
kovariant, contravariant und invariant einführen.
Die Typen der Felder eines Records verhalten sich zu dem Typ des Records kovariant.
Bekommen die Felder einen spezielleren Typ wird auch der Typ des Records spezieller.
Die Rückgabetypen einer Funktion verhalten sich kovariant zum Typ der Funktion.
Die Parametertypen einer Funktion verhalten sich contravariant zu dem Typ der Funktion.
In anderen Worten speziellere Funktionen dürfen allgemeinere Parameter haben.
Die meisten objektorientierten Programmiersprachen (seit Version 1.5 auch Java) unterstützen
kovariante Rückgabetypen von dynamisch gebundenen Methoden. Dies ermöglicht es zum Beispiel
die
Nehmen wir einmal an wir hätten ein Konstrukt für veränderbare Arrays eingeführt.
Hier wären die Argumenttypen invariant zum Typ des Arrays.
Grund ist, dass sonst Elemente eines falschen Typs in ein Array eingefügt werden
könnten. Die Sprache Java unterstützt kovarianz bei Arrays, was zu
Laufzeittypfehlern führt:
Die falsche Subtypregel in Java führt auch dazu, dass Arrays nicht so effizient
arbeiten können, wie das normalerweise möglich wäre. Bei jedem Einfügen eines
Elementes muss eine Laufzeittypprüfung stattfinden. Darüberhinaus gestaltet
sich das Zusammenspiel von Java 1.5 Generics und Arrays aufgrund dieser Subtypregel
problematisch.
Joins und Meets
Ein Typ
Ein Typ
In unserem Kalkül gibt es für zwei beliebige Typen imme einen Join. So ist
beispielsweise
Joins können dazu benutzt werden einen Typ für bedingte Ausdrücke zu bestimmen. Der Ausdruck
selOrt=(λx:{strasse:String, ort:String}. (x.ort))
so wird selOrt {strasse="Feldstraße 143",ort="22880 Wedel"} wie folgt
ausgewertet:
selOrt {strasse="Feldstraße 143",ort="22880 Wedel"}
(λx:{strasse:String, ort:String}. (x.ort)) {strasse="Feldstraße 143",ort="22880 Wedel"}
{strasse="Feldstraße 143",ort="22880 Wedel"}.ort
"22880 Wedel"
{u1={u2=unit}} den
Typ {u1:{u2:Unit}}
Ergänze die Auswertungsregeln, damit Exceptions aus den Records rauskommen können.
[Lösung]
try {x=(λx:Unit.x)error} onError {x=unit}
try {x=error} onError {x=unit} <-- hier geht es nicht mehr weiter
Subtypen
selOrt Funktion aus dem letzten Abschnitt. Sie hat den Typ
{strasse:String, ort:String} → String. Nehmen wir
einmal an Globalisierungssbestrebungen in unserem Unternehmen hätten
dazu geführt, dass wir von nun an einige Adressen mit einem zusätzlichen Länderkennzeichen
bestücken. Diese hätten dann zum Beispiel den Typ
{strasse:String, ort:String, land:String}. Unsere wertvolle
selOrt Funktion würde mit diesen neuen Adressen nicht mehr funktionieren. Es würde
zu einem Typfehler kommen, obwohl eigentlich alle nötigen Informationen zur Verfügung stehen.
Es wäre schön, wenn man auch mehr Informationen als gefordert liefern könnte, ohne
das es zu einem Typfehler kommt. In anderen Worten wenn das Argument einer Funktion einen
spezielleren Typ als gefordert haben dürfte. Diese Intuition wollen wir im folgenden mit
Hilfe einer operationalen Semantik formalisieren.

Top (Regel 3). Wir
werden noch Gründe für das Einführen des Typs Top kennenlernen. Intuitiv
entspricht er der Klasse Object, wie wir sie zum Beispiel aus Java kennen.
Die Formulierung
der zweiten Regel ist ausserordentlich elegant, macht eine direkte Umsetzung in einem
Typprüfer allerdings unmöglich, da wir einen beliebigen Typ U raten
müßten. Aus diesem Grund wird unsere Formulierung auch als deklarativ bezeichnet.
Für die konkrete Umsetzung müßten wir zunächst ein algorithmisches Subtyping-Regelwerk
entwickeln.
(λx:{strasse:String, ort:String}. (x.ort)) {strasse="Feldstraße 143",ort="22880 Wedel", land="D"}
Beispiel: Unit <: Top und {x:Unit,y:Unit} <: {x:Top,y:Unit}.
Beispiel: {name:String,strasse:String} <: {name:String} und
Unit→{name:String,strasse:String} <: Unit→{name:String}
Beispiel: {name:String,strasse:String} <: {name:String} und
{name:String}→Unit <: {name:String,strasse:String}→Unit
clone()-Methode einer Klasse mit einem konkreteren Rückgabetyp als
den der Basisklasse zu versehen. Die Programmiersprache Eiffel unterstützt entgegen
der typtheoretischen Bedenken kovariante Parametertypen. Dies kann in der Praxis
zu Laufzeittypfehlern führen, die auch als catcalls (lustiges Wortspiel, ohne
Übersetzung) bezeichnet werden.
Technisch:
[U]<:[T] ≡ (U<:T ∧ T<:U) .
Beispiel: [{x:Unit,y:Unit}] <: [{y:Unit,x:Unit}] aber nicht
[{x:Unit,y:Unit}] <: [{x:Unit}]
class BrokenArray {
public static void main(String [] argv) {
String [] strings = {"Hallo", "Welt"};
Object [] objects = strings;
objects[0]=new Integer(5);
}
}
Exception in thread "main" java.lang.ArrayStoreException
at BrokenArray.main(brokenarray.java:5)
J wird als Join der Typen S und T bezeichnet (J=S∨T)
wenn S<:J und T<:J und fur alle Typen U mit
S<:U und T<:U gilt: J<:U.
M wird als Meet der Typen S und T bezeichnet (M=S∧T)
wenn M<:S und M<:T und fur alle Typen L mit L<:S und L<:T gilt:
L<:M.
{x:Unit} ∨ {y:Unit} = {} oder
{x:unit} ∨ Unit→Unit = Top. (Dieses Beispiel zeigt
einen Nutzen vom Typ Top). Der Join muss allerdings nicht eindeutig
sein. So sind beispielsweise {x:Unit,z:Unit} und {z:Unit,x:Unit}
Join der Typen {x:Unit,z:Unit} und {x:Unit,y:Unit,z:Unit}.
if b then t else u würde den Typ T∨U bekommen. In Java
bekommt der Ausdruck b ? t : u den Typ T, wenn U<:T und den
Typ U wenn T<:U. Gilt weder U<:T noch T<:U
ist der Ausdruck falsch getypt. Grund dafür ist, dass es in Java für zwei beliebige Typen
keinen Join gibt. Erben die Klassen A und B jeweils von den Interfaces I und J (
wobei weder I von J erbt, noch umgekehrt), dann
haben sie die gemeinsamen Übertypen I, J und Object. Object kann nicht der Join
von A und B sein, da Object nicht spezieller als I ist. I kann nicht der Join sein, da
I nicht spezieller als J ist. J kann nicht der Join sein, da J nicht spezieller als I
ist. Folglich haben A und B keinen Join.