Einleitung | Operationale Semantiken | Ungetyptes λ-Kalkül | Einfach getyptes λ-Kalkül | Erweiterungen | Ausblick/Sourcen/Literatur



Das einfach getypte λ-Kalkül

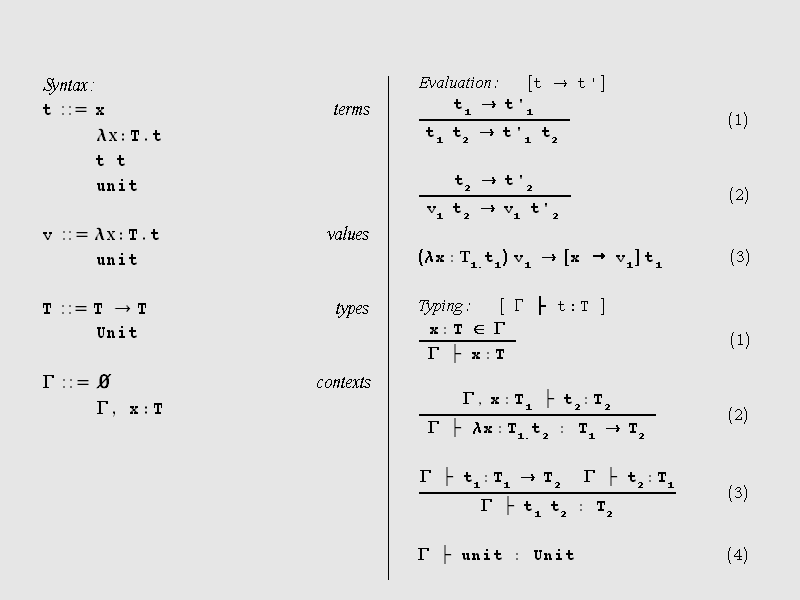
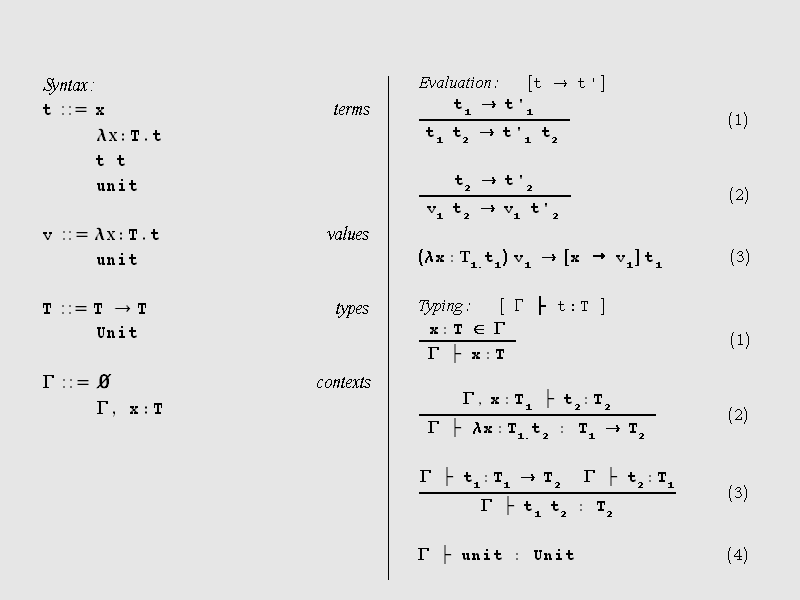
Operationale Semantik - Einfach getyptes Lambda-Kalkül

Nachdem wir bereits Erfahrung mit operationalen Semantiken gemacht haben, können wir das einfach getypte λ-Kalkül nun gleich anhand seiner operationalen Semantik erklären. Im Vergleich zum ungetypten λ-Kalkül sind die Terme praktisch die gleichen geblieben. Es wurde nur ein primitiver Wert unit ergänzt und eine Typzuweisung für das Argument in die Funktionsabstraktion aufgenommen (λx:T.t). Die Auswertungsfunktion hat sich nicht geändert.

Es gibt nun eine beliebig große Anzahl von konkreten Typen T wie zum Beispiel: 
Unit
Unit -> Unit
Unit -> (Unit -> Unit)
(Unit -> Unit) -> Unit
Unit -> (Unit -> (Unit -> Unit))
Unit -> ((Unit -> Unit) -> Unit)
(Unit -> Unit) -> (Unit -> Unit)
(Unit -> (Unit -> Unit)) -> Unit
((Unit -> Unit) -> Unit) -> Unit
...
T1→T2→T3 steht hierbei per Konvention für T1→(T2→T3). Der sogenannte Typ-Kontext Γ beschreibt alle Variablen-Typ Bindungen für einen bestimmten Ausdruck. Γ, x:T steht per Konvention für Γ ∪ {x:T}. Γ |- t : T wird gelesen als im Kontext Gamma hat der Term t den Typ T. Mit jeder Funktionsabstraktion wird dem Kontext Γ eine Variable-Typ Bindung x:T hinzugefügt.

Betrachten wir nun die Typregeln. Das Axiom (4) besagt, dass der Wert unit in jedem Kontext den Typ Unit hat. Regel (1) besagt, dass die Variable x im Kontext Γ den Typ T hat, wenn es im Kontext Γ eine Variable-Typ Bindung x:T gibt. Diese Regel mag zunächst obsolet erscheinen. Sie ist jedoch notwendig als Brücke zwischen Variablen, deren Typbindungen Elemente des Kontexts sind, und allgemeinen Termen, deren Typen sich aus dem Kontext berechnen lassen. Regel (2) beschreibt die Funktionsabstraktion. Innerhalb der Funktion (in der Prämisse) gibt es die Variable Typ-Bindung x:T. Ausserhalb der Funktion ist die Variable x nicht mehr an den Typ T gebunden. Regel (4) beschreibt die Funktionsapplikation. Zu beachten ist die Verwendung der Metavariablen T1 in der Prämisse.

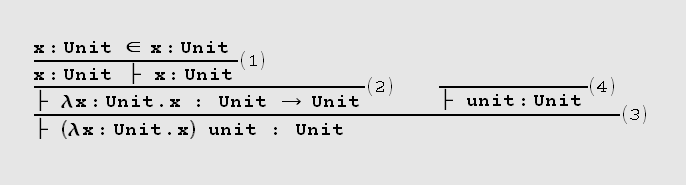
Wir können nun ganz mechanisch einen Typableitungsbaum für den Term (λx:Unit.x) unit konstruieren: Typableitungsbaum 1

Über den Bruchstrichen steht jeweils die Prämisse unter den Bruchstrichen die Folgerung. Neben jedem Bruchstrich steht die Nummer der angewendeten Regel. Die Folgerungen der vorangegangenen Regeln bilden die Prämisse für die nächste Regel. _ |- steht für {} |-. Klammern wurden bei Bedarf ergänzt.

Terme für die ein Typableitungsbaum existiert bezeichnen wir als wohlgetypt.

Vergleichen wir die Eigenschaften des einfach getypten λ-Kalküls mit den Eigenschaften des ungetypten λ-Kalküls

Werte sind in Terme in Normalform:
Gilt aus den gleichen Überlegungen wie im ungetypten Fall.

Jeder Term in Normalform ist ein Wert:
Gilt aus den gleichen Überlegungen wie im ungetypten Fall.

Die Auswertung (→) erfolgt deterministisch:
Gilt aus den gleichen Überlegungen wie im ungetypten Fall.

Jeder wohlgetypte Term hat eine Normalform:
Diese Eigenschaft gilt für dieses Kalkül wieder (ohne Beweis). Natürlich ist es keine allgemeine Eigenschaft von typisierten Sprachen, dass ihre Programme immer terminieren. In unserem Fall ist die Terminierung eine Folge der verringerten Ausdruckskraft im Vergleich zum ungetypten Kalkül.

Zur Veranschaulichung betrachten wir den Term: 
λx:?.x x
Es wird uns nicht gelingen einen Typ für x zu bestimmen. Hat x beispielsweise den Typ U muss es nach Regel (3) auch den Typ U→T haben. Das geht aber nicht. Also hat x keinen Typ.

Wir wollen nun zwei weitere Eigenschaften betrachten, die zusammengenommen die Typsicherheit ausmachen.

Progress (Fortschritt):
Wohlgetypte Terme sind entweder in Normalform (d.h. sie sind Werte) oder sie können noch einen Auswertungsschritt durchlaufen (d.h. es gibt ein t' so dass t→t').

Preservation (Typerhaltung):
Der Typ eines Terms bleibt bei jedem Auswertungsschritt erhalten (d.h. wenn t im Kontext Γ den Typ T hat und es ein t' mit t→t' gibt, dann hat t' im Kontext Γ auch den Typ T).

Beide Eigenschaften gelten für unsere Sprache.



Implementierung in Haskell 

module Simple (ctxEmpty, Term, typeof, eval, safeEval)
  where

data Type = TyUnit | TyArrow Type Type
  deriving (Show,Eq)

data Term = TmUnit | TmVar String | TmAbs String Type Term | TmApp Term Term
  deriving Show

data Context = Context [(String, Type)] deriving Show

ctxEmpty :: Context 
ctxEmpty  = Context []

addBinding             :: Context -> String -> Type -> Context
addBinding (Context c) s t = (Context ((s,t):c))

getBinding             :: Context -> String -> Type
getBinding (Context ((n,t):cs)) s = if n==s then t else getBinding (Context cs) s                                    
getBinding (Context [])     s = error $ "Name "++" nicht bekannt" 

typeof :: Context -> Term -> Type
typeof _   TmUnit          = TyUnit                                     -- Axiom (4)
typeof ctx (TmVar s)       = getBinding ctx s                           -- Regel (1)
typeof ctx (TmAbs s ty1 t) = let ctx' = addBinding ctx s ty1            -- Regel (2)
                                 ty2  = typeof ctx' t
                             in TyArrow ty1 ty2   
typeof ctx (TmApp t1 t2)   = let (TyArrow ttp tte) = typeof ctx t1      -- Regel (3)
                                 tta               = typeof ctx t2
                              in if tta==ttp then tte 
                                 else error ("Argumenttyp "++show tta++
                                             " passt nicht zu Parametertyp "++show ttp)  


eval :: Term -> Term
eval TmUnit                   = TmUnit
eval (TmApp (TmAbs s _ t) t2) = eval (substTm t s (eval t2))   
eval (TmApp t1 t2)            = eval $ TmApp (eval t1) t2 
eval (TmVar s)                = error $ "freie Variable: " ++ s
eval abs@(TmAbs _ _ _)        = abs

substTm :: Term -> String -> Term -> Term
substTm var @(TmVar n1)       n t = if n1==n then t else var
substTm fAbs@(TmAbs n1 ty t1) n t = if n1==n then fAbs
                                    else (TmAbs n1 ty (substTm t1 n t))
substTm       (TmApp t1 t2)   n t = TmApp (substTm t1 n t) (substTm t2 n t)
substTm        rest           _ _ = rest

-- eval mit Typprüfung:
safeEval :: Term -> Term
safeEval t = eval $ const t $! (typeof ctxEmpty t)
Den Datentyp Term haben wir um den Konstruktur TmUnit für den Wert unit und eine Typangabe im Konstruktor erweitert. Typen werden durch den Datentyp Type repräsentiert. Der Kontext Γ wird durch eine Liste aus Variablen-Name und Typ Tupeln repräsentiert. Die Funktionen eval und SubstTm sind bis auf den Fall TmUnit unverändert zur Implementation im ungetypen λ-Kalkül.

Neu hinzugekommen ist die Funktion typeof. Für jeden wohlgetypten Ausdruck liefert sie den Typ. Enthält ein Ausdruck einen Typfehler entsteht eine Exception. In der Zeile (TyArrow ttp tte) = typeof ctx t1 wird dem Ergebnis der Typberechnung das Muster (TyArrow _ _) aufgedrückt. Passt das Muster nicht (d.h. ist der rechte Term einer Funktionsanwendung keine Funktion) generiert die Laufzeitumgebung eine relativ unverständliche Fehlermeldung. Die Fehlermeldungen sind insgesamt verbesserungsfähig. Von einem echten Typprüfer würden wir uns mehr Informationen darüber wünschen, wo genau ein Fehler aufgetreten ist.

Neu hinzugekommen ist die Funktion safeEval die vor der Auswertung eines Terms eine Typprüfung erzwingt. Das eigentliche eval ignoriert Typen.

Übung: Male einen Typableitungsbaum für den Ausdruck (λx:U→U.x unit)(λx:U.x) Für Unit sollte dabei einheitlich U geschrieben werden. [Lösung]