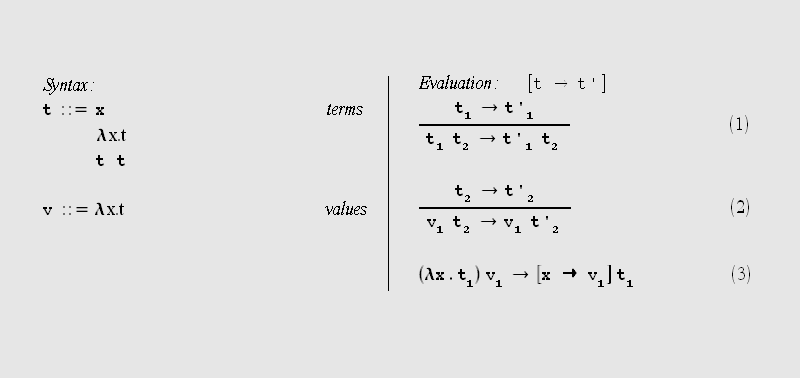
Lambda Terme können mit der folgenden abstrakten Syntax beschrieben werden:
|
Der Lambda-Term λx.x kann auch Identitätsfunktion genannt werden.
Er entspricht f(x)=x. x bezeichnen wir in diesem Term als
gebundene Variable. Sie ist an die Funktionsabstraktion λx.x
gebunden.
Der Lambda-Term λx.y kann auch konstante Funktion genannt werden.
Er entspricht f(x)=y. y bezeichnen wir in diesem Term als
freie Variable, da sie an keine Funktionsabstraktion gebunden ist. Wir werden im folgenden
freie Variablen verbieten und nur sogenannte geschlossene Terme betrachten. Geschlossene
Terme sind Terme ohne freie Variablen. Eine konstante Funktion als geschlossener Term
ist beispielsweise λx.(λy.y). Auch in diesem Kalkül dürfen wir
wieder Klammern für konkrete Terme verwenden, auch wenn diese nicht Bestandteil der
abstrakten Syntax sind. Im Gegensatz zu der letzten betrachteten Sprache dienen die Klammern
hier nicht nur der Lesbarkeit. So ist zum Beispiel die Funktionsapplikation f1 (f2 f3)
nicht identisch mit der Applikation (f1 f2) f3. Per Konvention wollen wir
f1 f2 f3 lesen als (f1 f2) f3. Wir sagen: Funktionsapplikation ist
links-assoziativ.
Funktionen mit zwei Argumenten können wir als geschachtelte Funktionen verstehen. Wendet man
auf die Funktion das erste Argument an wird eine Funktion als Ergebnis geliefert, auf die
wir das zweite Argument anwenden können um dann das Ergebnis zu erhalten. So läßt sich
beispielsweise die Funktion f(x,y)=x schreiben als λx.λy.x
Betrachten wir nun die folgende operationale Semantik für das ungetypte λ-Kalkül:
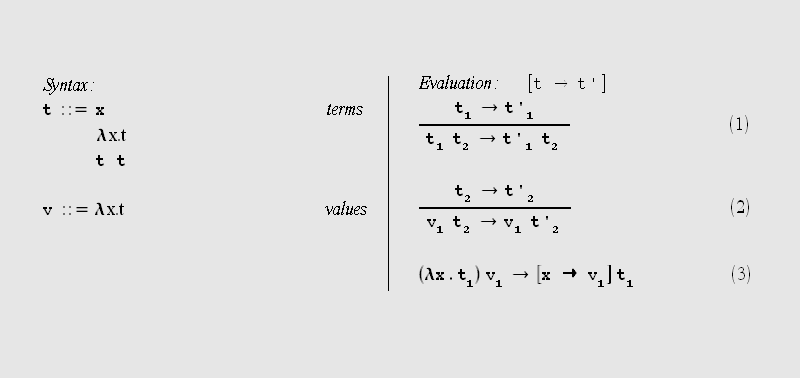
Da wir freie Variablen ausgeschlossene haben und Funktionsabstraktionen als Werte
betrachten müßen wir bei der Auswertung nur noch den Fall Funktionsapplikation
betrachten. Genau wie in dem Beispiel mit den Boolschen Ausdrücken ist hier auch
wieder eine eindeutige Auswertungsreihenfolge durch die operationale Semantik beschrieben.
Es wird immer von links nach rechts und von Aussen nach Innen ausgewertet. Mit der
Regeln (1) wird gesteuert, dass zunächst der linke Term t1 zu einem
Wert ( und das ist immer eine Funktionsabstraktion) ausgewertet wird. Sobald der linke
Term ein Wert ist kann der rechte Term reduziert werden (Regel (2) ). Danach folgt das Einsetzen mittels
Regel (3).
Wie das Einsetzten genau funktioniert sei hier nur grob umrissen. Das genaue Verfahren
werden wir anhand der Haskell-Implementierung zeigen. Wichtig ist, dass alle Vorkommen
der Variable x im Term t1 durch den Wert v1 ersetzt werden,
ausgenommen solche die durch eine neue Funktionsabstraktion neu gebunden wurden.
Beispiel: [x → v]((λx.x)x)=((λx.x)v)
Dadurch, dass wir nur geschlossene Terme betrachten, umgehen wir einige Probleme wie
zum Beispiel die Gefangennahme von freien Variablen (variable capture). Wer mehr
darüber wissen will, kann in der Literaturliste schlau werden.
Betrachten wir nun die beispielhaft die folgenden Definitionen:
|
Wir können nun den Ausdruck not true gemäß der operationalen Semantik auswerten.
|
Vergleichen wir die Eigenschaften des ungetypten λ-Kalküls mit den Eigenschaften der Sprache für Boolsche Ausdrücke:
Werte sind in Terme in Normalform:
Gilt auch hier: Werte sind per Definition Funktionsabstraktionen. Wir kennen aber
nur Ableitungsregeln für Funktionsapplikationen. Es läßt sich somit aus einem
Wert kein weiterer Ausdruck mehr ableiten.
Jeder Term in Normalform ist ein Wert:
Gilt auch hier. Eine einzelne Variable kann kein Term sein, da wir freie Variablen
nicht zulassen. Für jede Funktionsapplikation gibt es noch eine Ableitungsregel.
Läßt sich ein Term nicht weiter ableiten muss somit eine Funktionsabstraktion,
also ein Wert vorliegen.
Die Auswertung (→) erfolgt deterministisch:
Gilt auch hier. Wie wir bereits beschrieben haben ist die Auswertungsreihenfolge durch die operationale
Semantik eindeutig bestimmt.
Jeder Term hat eine Normalform:
Diese Eigenschaft gilt nicht mehr. Betrachten wir als Beispiel den folgenden Term,
der in der Literatur Omega-Kombinator genannt wird:
|
omega ergibt sich omega selbst.
Es kommt somit nie zu einer Normalform. Man sagt auch omega divergiert.
Tatsächlich ist das ungetype λ-Kalkül mächtig genug, um jeden beliebigen Algorithmus
damit zu beschreiben. Für allgemeine Rekursion greift man nicht auf den omega-
Kombinator sondern auf sogenannte Fixpunkt-Kombinatoren zurück, die es ermöglichen
rekursive Funktionen mit Abbruchsbedingung zu formulieren.
Implementierung in Haskell
|
Die Implementation entspricht hier wieder recht genau der operationalen Semantik. Die abstrakte Syntax für Terme wird durch den Datentyp Term repräsentiert. Bei der Evaluation fasst die erste Gleichung Regel (2) und Axiom (3) zusammen. Die zweite Gleichung setzt Regel (1) um. Die dritte Gleichung prüft auf freie Variablen. Diese Prüfung ist nicht ausreichend um sicherzugehen, dass der Term keine freien Variablen enthält. Die vierte Gleichung behandelt wieder die Normalform.
Die Einsetzoperation [x→v]t heisst hier substTm t x v. Wir hatten diese Operation
bisher nur ungenau beschrieben. Es werden rekursiv alle Vorkommen der Variable mit dem Namen n ersetzt
durch den Term t. Mit if n1==n then fAbs in der zweiten Zeile wird geprüft,
ob der gleiche Variablenname in einer neuen Funktionsabstraktion neu gebunden wird.
Nun können wir definieren:
|
|
Übung: Es darf keine freien Variablen geben, damit die substTm
Funktion richtig arbeitet. Dies wird bisher aber nur unzureichend geprüft. Schreibe
eine Funktion hasFV :: Term -> [String] -> Bool, die genau
dann true liefern soll, wenn es freie Variablen gibt. In der String-Liste
sollen die Namen der schon gebundenen Variablen gespeichert sein. Die Liste
ist beim ersten Aufruf leer. [Lösung]