Constraint Domains sind in zwei Kategorien einzuteilen, in endliche und unendliche Domains. Während bei unendlichen Domains die Variablen unendlich viele Zustände annehmen können, haben Variablen mit endlichen Domains nur eine begrenzte Anzahl an Zuständen. Unendliche Domains sind zum Beispiel Domains mit dem Wertebereich Integer oder Real. Im Verlauf dieser Arbeit wird allerdings nur noch auf endliche Wertebereiche eingegangen und unendliche Domains vernachlässigt.
| :- lib(fd). |
| oder |
| :- use_modul(libary(fd)). |
Folgende wichtige Regeln aus der fd-Bibliothek sollen an dieser Stelle kurz vorgestellt werden, um das Verständnis zukünftiger Beispiele zu gewährleisten.
| labeling(Liste) |
| member(Element, Liste) |
| alldistinct(Liste) |
Natürlich muss auch erklärt werden, wie man Variablen endliche Wertebereiche zuordnet. Um beispielsweise einer einzelnen Variablen als Wertebereich ein Integerintervall von eins bis drei zuzuordnen, gibt man Folgendes an:
| X :: 1..3 |
Natürlich muss kein Intervall vorliegen. Möchte man der Variablen X einen Wertebereich mit Lücken zuordnen, so ist dies auch simpel zu bewerkstelligen.
| X :: [1,3,42] |
Um mehreren Variablen den gleichen Wertebereich zuzuordnen muss man diese nur in eckige Klammern setzen.
| [X, Y, Z] :: 1..3 |
Wie wir später in Beispielen sehen werden, ist es häufig von Vorteil eine Liste mit Variablen als Elemente zu deklarieren. Dies vereinfacht beispielsweise den Aufruf der labeling-Regel.
| Liste = [X ,Y, Z], Liste :: 1..3 |
Um primitive Constraints aufstellen zu können, fehlen nun noch die Vergleichsoperatoren. Bei diesen steht auf der linken Seite immer eine Variable, die rechte Seite kann ein beliebig komplexer Ausdruck gemäß der Definition für primitive Constraints sein.
| #= | -> | ist gleich |
| #' | -> | ungleich |
| #> | -> | echt größer |
| #>= | -> | größer gleich |
| #< | -> | echt kleiner |
| #<= | -> | kleiner gleich |
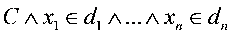
Zu unterscheiden sind hierbei allerdings noch lokale und globale primitive Constraints. Lokale primitive Constraints beeinflussen nur den Wertebereich einer Variablen und sind somit unäre Constraintatome. Globale primitive Constraints beeinflussen die Domains mehrerer Variablen. Während lokale Constraintatome den Suchbaum zur Compilezeit beschneiden, können die globalen primitiven Constraints erst zur Laufzeit überprüft werden, in dem die möglichen Lösungen im Suchraum abgearbeitet werden.
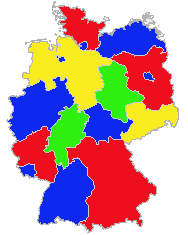
Das CSP soll nun an einem ersten praktischen Beispiel im ECLiPSe-System gezeigt werden. Hierfür wurde das Problem der Landkartenfärbung gewählt. Die
Bundesländer Deutschlands sollen so gefärbt werden, dass sich nie ein und die selbe Farbe berührt, man aber möglichst wenig Farben benötigt.

Um dieses CSP lösen zu können, definiert man zuerst eine Liste, die Variablen für alle 16 Bundesländer enthält.
| Laender = [BW, BY, BE, BB, HB, HH, HE, MV, NI, NW, RP, SL, SN, ST, SH, TH] |
Jeder dieser Variablen soll eine von 4 Farben zugewiesen werden. Da mit Hilfe der fd-Bibliothek jedoch nur numerische Probleme gelöst werden können, wird jede Farbe durch eine Integerzahl substituiert und der daraus resultierende Wertebereich der Liste zugewiesen. 1 steht für Blau, 2 für Rot, 3 für Grün und Vier für Gelb.
|
% Domain für Länderfarben, wobei % 1: blau % 2: rot % 3: grün % 4: gelb Laender :: 1..4 |
Im nächsten Schritt müssen die primitiven Constraints aufgestellt werden. Hierbei gilt, dass die Variablen der sich berührenden Bundesländer nicht den gleichen Wert annehmen dürfen. Zum Abschluss wird die labeling-Regel aufgerufen, um die Variablen mit Werten gemäß ihrer Domain und den Constraints zu belegen.
|
BW ## BY, BW ## HE, BW ## RP, BY ## HE, BY ## TH, BY ## SN, BE ## BB, BB ## MV, BB ## NI, BB ## SN, BB ## ST, HB ## NI, HH ## NI, HH ## SH, HE ## NI, HE ## NW, HE ## RP, HE ## TH, MV ## NI, MV ## SH, NI ## NW, NI ## ST, NI ## SH, NI ## TH, NW ## RP, RP ## SL, SN ## ST, SN ## TH, ST ## TH, labeling(Laender) |
Wird das erstellte Programm nun im ECLiPSe-System kompiliert und ausgeführt, erhält man mehrere Lösungen. Die erste gefundene Lösung sei an dieser Stelle graphisch dargestellt.