Suchstrategien
... [ Seminar "Programmierkonzepte und Programmiersprachen" ]
... [ Inhaltsverzeichnis ]
... [ zurück ]
... [ weiter ] ...
Übersicht: Titel
Klassifizierung
Zur Ermittelung einer oder mehrerer Lösungen wenden Constraintsolver, wie sie beispielsweise im ECLiPSe-System zum Einsatz kommen, verschiedene
Suchstrategien im Ergebnisraum an. Diese können zuerst in constructive und moved-based Algorithmen unterschieden werden.
Bei constructive Algorithmen erfolgt eine inkrementelle Wertezuweisung an die Variablen. Dies impliziert, dass der Suchraum anhand einer Baumstruktur
organisiert wird. Moved-based Algorithmen arbeiten hingehen mit total assignments, also mit zeitgleichen Zuweisungen von Werten an alle Variablen. Der Suchraum wird
hierbei durch methodische Modifikation einzelner Problemvariablen ausgehend von vorherigen Zuweisungen untersucht, soll heißen, dass daraus neue total
assignments abgeleitet und getestet werden, bis eine oder alle Lösungen gefunden worden sind. Diese Art der Suche erweist sich jedoch als sehr
speicherintensiv, da alle überprüften möglichen Lösungen gemerkt werden müssen. Gerade bei sehr komplexen Problemen kann dies zu Schwierigkeiten führen.
Im weiteren Verlauf werden nur noch constructive Algorithmen betrachtet.
Die Suchstrategien können zudem noch nach vollständiger und unvollständiger Suche klassifiziert werden. Bei der vollständigen Suche wird der gesamte
Suchbaum traversiert. Dies ist beispielsweise bei der Suche nach der optimalen Lösung notwendig. Hingegen wird bei der unvollständigen Suche nur ein Teil des
Suchbaums betrachtet. So kann bei sehr komplexen Aufgabenstellungen die zulässige Anzahl an Rücksprüngen (auf Rücksprünge wird im
Folgenden noch näher eingegangen) angegeben werden. Sollte bis dahin noch keine Lösung gefunden worden sein, wird die Suche abgebrochen.
Generate and Test
"Generate and Test" stellt die einfachste Suchstrategie dar. Hierbei handelt es sich um die einfache Tiefensuche von links nach rechts im Suchbaum. Alle
Variablen werden mit Werten gemäß ihrer Domain belegt. Danach erfolgt die Überprüfung, ob alle aufgestellten Bedingungen eingehalten werden. Ist dies
nicht der Fall, wird die nächst mögliche Wertekombination im Baum gewählt. Da alle möglichen Wertkombinationen im Baum von links nach rechts abgearbeitet
werden müssen, ist dies sehr laufzeitintensiv und der Aufwand steigt mit jeder Variablen exponentiell an.
Schematische Darstellung von "Generate and Test"
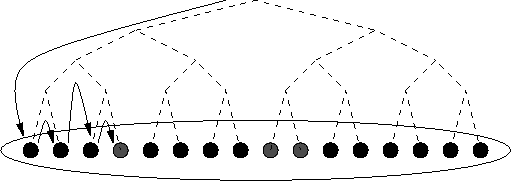
In obiger Grafik repräsentiert jeder Knoten für eine Problemvariable, jede Kante für einen Wert, den die Problemvariable annehmen kann und jeder Punkt für eine
mögliche Wertkombination. Das Prinzip der Tiefensuche wird auch in den anderen vorgestellten Suchstrategien verwendet, es erfolgt allerdings jeweils eine
Weiterentwicklung, um effizienter zu einer möglichen Lösung zu gelangen.
Backtracking
Beim Backtracking erfolgt eine schrittweise Belegung der Variablen mit Werten aus ihren Wertebereichen, dass heißt, dass der ersten Variablen ein Wert aus
ihrer Domain zugewiesen wird und danach sofort überprüft wird, ob die Teillösung gegen ein primitives Constraint verstößt. Falls kein Verstoß vorliegt, wird
der nächsten Variablen ein Wert zugewiesen und es erfolgt wieder eine Überprüfung auf Verstoß gegen ein Constraintatom. Sollte ein Verstoß vorliegen, wird
die Variable mit dem nächsten Wert aus der Domain belegt. Für den Fall, dass der Wertebereich der Variablen erschöpft ist, erfolgt ein Rückschritt zur nächst
höheren Variablen im Suchbaum, welche dann mit einem neuen Wert belegt wird. Hierbei wird der Suchbaum beschnitten, da Variablen unter der aktuellen
Variablen mit keinen Werten belegt werden. Man spricht in diesem Fall auch von Pruning (engl.: to prune: beschneiden). Sollte der Wertebereich der Variablen erschöpft
und auch kein Rückschritt mehr möglich sein, da man sich am obersten Baumknoten befindet, gibt es keine Lösung für das betrachtete Problem. Die im
vorherigen Kapitel vorgestellte labeling-Regel der fd-Bibliothek arbeitet mit diesem Suchalgorithmus.
Das Backtracking soll an folgendem einfachen Beispiel verdeutlicht werden.
:- lib(fd).
solve(Triple) :-
Triple = [X, Y ,Z],
[X, Z] :: 1..2,
Y :: 1..3,
X #> 1,
Y #>= X,
Z #< Y,
labeling(Triple).
|
Der Suchbaum sieht in diesem Fall folgendermaßen aus:
Suchbaum Backtracking
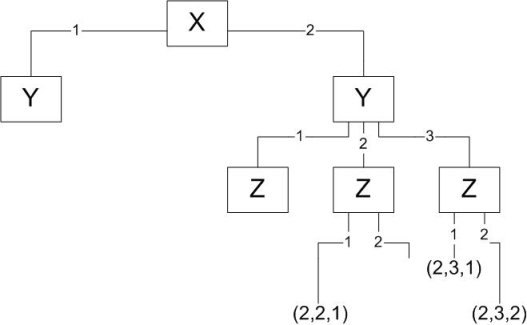
Zur Erklärung: Die erste Variable, X, wird mit dem ersten Wert aus ihrer Domain belegt (1). Da dieser Wert jedoch auch gegen das erste Constraintatom
verstößt, wird der nächste Wert aus der Domain gewählt. Somit wird zugleich der linke Teilbaum abgeschnitten, sodass bereits nach der ersten Variablenbelegung
die Hälfte aller möglichen Lösungen ausgeschlossen werden kann. Die oben beschriebene Systematik wird nun weiter verfolgt, bis man zur ersten Lösungsmenge
(2,2,1) gelangt. Um hiernach eine weitere Lösung zu erhalten, muss darauf ein Rückschritt von der bereits belegten Variable Z zu der Variablen Y erfolgen,
welche nun mit 3 belegt wird. Aus dieser Position werden dann durch Belegen der Variablen Z die anderen beiden Lösungen gefunden.
Forward Checking
Das Forward Checking ist eine Erweiterung des normalen Backtrackings, die zu einer enormen Effizienzsteigerung in der logischen Programmierung mit
Einschränkungen führen kann. Hierbei wird zuerst einer Variablen abermals ein Wert zugewiesen und diese Zuweisung anhand des Constraint überprüft. Darauf
erfolgt die dynamische Anpassung der Domains der zukünftigen Variablen. Dass heißt, dass alle Werte der Domains, die mit dieser Zuweisung in Konflikt stehen,
temporär aus dem Wertebereich gelöscht werden. Somit wird sichergestellt, dass nur noch konsistente Werte in den Domains der noch zu behandelnen Variablen
sind. Sollte bei diesem Verfahren ein leerer Wertebereich einer zukünftigen Variablen auftreten, steht bereits zu einem gegebenenfalls sehr frühen Zeitpunkt
fest, dass dieser Ansatz zu keiner Lösung führen kann. Das Forward Checking nutzt daher das Constraint, um ein effizienteres Pruning durchführen zu können
als es beim reinen Backtracking der Fall ist.
Das Forward Checking soll an dieser Stelle an obigem Beispiel nochmals kurz verdeutlicht werden. Unter der Annahme, dass X mit 2 belegt ist, wird der Wert
1 aus der Domain der Variablen Y belegt. Hierdurch wird der Baum schon ohne die Belegung von Y weiter beschnitten.
Heuristik
Bis jetzt wurde der Aufbau des Suchbaums noch nicht näher betrachtet. Es wird davon ausgegangen, dass die Variablen in der Reihenfolge ihrer Definition im
Programm verwendet werden. Auch wird davon ausgegangen, dass die möglichen Werte der Variablen in der Reihenfolge ihres Auftretens in der Domain verwendet
werden. Beides muss nicht zwangsläufig der Fall sein. In den folgenden beiden Punkten wird gezeigt, wie eine dynamische Variablen- und Werteauswahl zur
Effizienzsteigerung beitragen kann, aber auch, wie bereits zur Entwurfszeit die spätere Laufzeit minimiert werden kann.
Variablenordnung
Die Variablenordnung beschreibt, in welcher Reihenfolge die Variablen im Suchbaum auftreten. Die Änderung der Reihenfolge bewirkt unter Umständen auch die
Änderung der Anzahl der Knoten im Suchbaum. Die Variablenordnung kann statisch zur Entwurfszeit festgelegt oder aber dynamisch zur Laufzeit berechnet
werden. Während die statische Festlegung beim reinen Backtracking Anwendung findet, kann die dynamische Auswahl von Variablen erst sinnvoll beim Forward
Checking erfolgen. Dies beruht darauf, dass nur in diesem Fall neue Informationen über die jeweiligen Domains zur Verfügung stehen.
Generell soll die Variablenordnung nach dem Fail-First-Prinzip festgelegt werden. Dieses besagt: "Um erfolgreich zu sein, probiere das zuerst, was am
wahrscheinlichsten zum Fehler führt!". Hieraus leitet sich ab, dass immer die Variable gewählt werden soll, welche den kleinsten (im dynamischen Fall:
verbleibenden) Wertebereich hat. Für den Fall, dass mehrere Variablen gleich große Domains haben, so soll die Variable gewählt werden, welche am häufigsten
in den primitiven Constraints vorkommt.
In folgenden Beispiel soll verdeutlicht werden, wie die Variablenordnung zur Entwurfszeit das simple Backtracking beeinflussen kann.
Suchräume bei unterschiedlicher Variablenordnung
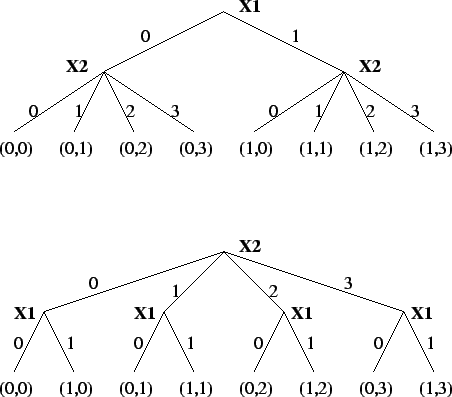
Würde man annehmen, dass in diesem Beispiel die Constraintatome
gelten, so wird ersichtlich, dass sich aufgrund einer überlegten Variablenordnung, welche sich an die oben aufgestellte Regel hält, eine Reduzierung der
notwendigen Backtrackingschritte bis zur erfolgreichen Lösung erreichen lässt.
Die dynamische Variablenordnung soll an dieser Stelle am Beispiel einer eigenen labelling-Regel "labelingff(Liste)" dargestellt werden, die die
Variablenauswahl berücksichtigt. Dies geschieht durch die Regel "deleteff(Vs, V, Rest)", welche über den Parameter V die Variable mit der kleinsten
Domain zurückgibt.
labelingff([]).
labelingff(Vs) :-
deleteff(Vs, V, Rest),
indomain(V),
labelingff(Rest).
deleteff([V0|Vs], V, Rest) :-
get_domain_size(V0, S0),
min_size(Vs, S0, V0, V, Rest).
min_size([], _, V, V, []).
min_size([V1|Vs], S0, V0, V, [V0|Rest]) :-
get_domain_size(V1, S1),
S1 #< S0
min_size(Vs, S1, V1, V, Rest).
min_size([V1|Vs], S0, V0, V, [V1|Rest]) :-
get_domain_size(V1, S1),
S1 #>= S0
min_size(Vs, S0, V0, V, Rest).
|
Werteordnung
Nach der Auswahl der Variablen erfolgt nun noch die Bestimmung, welcher Wert der Domain der Variablen als nächstes zugeordnet werden soll. Die Wertauswahl
erweist sich aber nur als sinnvoll anwendbar, wenn nur eine oder wenige Lösungen gesucht werden, da ansonsten so oder so alle Werte betrachtet werden müssen.
Abermals ist diese Systematik nur beim Forward Checking sinnvoll anwendbar, da man nur hierbei neue Informationen über die Werte(bereiche) der Variablen
erhält.
Die Auswahl kann nach verschiedensten Algorithmen erfolgen, welche sehr problemspezifisch gewählt werden sollten. So kann es in einem Fall von Vorteil
sein, die Domain aus der Mitte heraus nach außen hin abzuarbeiten. In anderen Fällen erscheint es aber auch vernünftig, die Kosten der Wertwahl durch den
Prozentsatz der vergefallenen Werte in den zukünftigen Domains zu berechnen und den Wert mit den geringsten Kosten zu nehmen. Daher kann an dieser Stelle
keine allgemein gültige Regel dem interessierten Leser vorgestellt werden.
... [ Seminar "Programmierkonzepte und Programmiersprachen" ]
... [ Inhaltsverzeichnis ]
... [ zurück ]
... [ weiter ] ...


