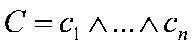Einführung in Einschränkungen
... [ Seminar "Programmierkonzepte und Programmiersprachen" ]
... [ Inhaltsverzeichnis ]
... [ zurück ]
... [ weiter ] ...
Übersicht: Einführung in Einschränkungen
Einleitung
Wenn man von der logischen Programmierung mit Einschränkung spricht, muss zuerst der Begriff "Einschränkung" geklärt werden. Einschränkungen
(engl.: constraints) sind Wert-, Rand- oder Nebenbedingungen, die die Eigenschaften und Beziehungen von teilweise unbekannten Objekten beschreiben.
Einschränkungen können beispielsweise als mathematische Gleichung oder als logisches Prädikat gesehen werden und formalisieren in vielen Problemstellungen
Nebenbedingungen der Lösungen. Da in der Literatur häufig der englische Terminus "Constraint" verwendet wird, übernimmt der Verfasser dies auch für diese
Ausarbeitung.
An einem einfachen Beispiel soll verdeutlich werden, wie Einschränkungen zur Lösung eines Problems führen können.
Ein Mathematiker hat die letzte Ziffer seines Zahlenschlosses am Fahrrad vergessen. Er versucht nun durch Einschränkungen sich an die Ziffer wieder zu
erinnern. Folgende Bedingungen kann er aufstellen:
- Einstellig: Da es sich nur um eine ganzzahlige Ziffer handeln kann.
-> 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Ungrade: Durch diese Bedingung werden alle geraden Zahlen aus dem Ergebnisraum entfernt.
-> 1, 3, 5, 7, 9
- Keine Primzahl: Alle Primzahlen werden aus dem Ergebnisraum gelöscht.
-> 1, 9
- Nicht die 1:
-> 9
Durch diese Bedingungen kommt der Mathematiker also zu der Lösung, dass die vergessene Ziffer nur 9 sein kann. Es wird aber auch deutlich, dass nur
aufgrund der Kombination der Bedingungen eine eindeutige Lösung möglich ist. Würde man zum Beispiel nur die zweite Einschränkung "ungrade" betrachten, so erhält man eine
unendliche Lösungsmenge.
Definition Constraint
Wenn von Constraints / Einschränkungen gesprochen wird, muss grundlegend in folgende zwei Fälle unterschieden werden:
Primitive Constraints / Constraintsatom
Primitive Constraints beschreiben die Beziehung zwischen Variablen und bestehen daher aus Variablen, einem Beziehungssymbol, gegebenenfalls einer oder
mehreren Konstanten und gegebenenfalls einer oder mehreren Funktion(en) des Wertebereiches. Auf diesen wird später noch genauer eingegangen.
Constraint
Unter Constraint versteht man die Konjunktion von primitiven Constraints. Dies lässt sich folgendermaßen darstellen:
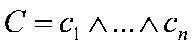
wobei:
C = Constraint
cn = primitives Constraint
Arität
Die Arität bezüglich primitiven Constraints gibt an, wie viele Variablen in einem Constraintatom auftreten. In einem unären Constraintatom tritt nur eine
Variable auf. In diesem Fall kann der Wertebereich der Variablen bereits im Präprozess verkleinert. Während der Laufzeit wird dann diese Einschränkung
ignoriert werden.
Bei einem binären Constraintatom treten zwei Variablen auf. Binäre primitive Constraints können als Graph dargestellt werden, in dem die Variablen durch
Knoten und die Beziehungen durch die Kanten repräsentiert werden. Für die folgende Abbildung gilt die Bedingung, dass alle Variablen paarweise
verschieden sein sollen.
Binäre Constraints
Darstellung als Graph
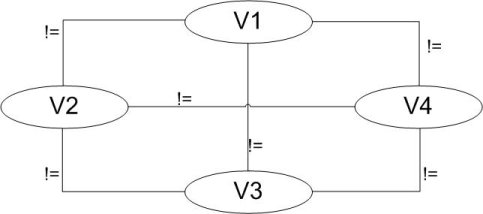
Primitive Constraints mit n Variablen werden als n-näre primitive Constraints bezeichnet. Diese können jeweils auf binäre Constraintsatome zurückgeführt
werden.
... [ Seminar "Programmierkonzepte und Programmiersprachen" ]
... [ Inhaltsverzeichnis ]
... [ zurück ]
... [ weiter ] ...