2. Funktionale Programmierung

[ XML und Haskell Seminar ] ... [ Thema XML Verarbeitung mit Haskell ] ... [ 3. XML Verarbeitung ]

Übersicht

2.1. Einleitung

In der Beschreibung des funktionalen Berechnungsmodells wird hervorgehoben, WAS berechnet wird, und nicht WIE eine Berechnung stattfindet. Man spricht hier auch von einem höheren Abstraktionsgrad.
In einem reinen funktionalen Programmierparadigma gibt es keinen Speicher, keine Variablen und somit auch keine Zustandstransformationen mehr.
Die Definitionen neuer Funktionen über Basisfunktionen oder bereits definierte Funktionen und die Anwendung von Funktionen (deshalb manchmal auch als applikative Programmierung bezeichnet) steht im Vordergrund. Eine Funktionsanwendung liefert einen Wert, der nicht in eine Speicherstelle geschrieben wird (Variablenzuweisung), sondern als Eingabe weiterer Funktionsanwendungen dienen kann (Einsetzungsschema). Selbst das Hauptprogramm ist dann nichts anderes als eine Funktion.
Iterationen, im imperativen Programmierparadigma meist durch ds Herunter- oder Heraufzählen einer Variablen gekennzeichnet, werden im funktionalen Ansatz durch Rekursion ersetzt.

Zwei wichtige FP Mechanismen, welche genutzt werden um XML Dokumente zu verarbeiten, sind Kombinatoren (combinators) und Funktionen höherer Ordnung.

In funktionalen Sprachen besteht ein Programm allein aus Abstraktion, das ist die Funktionsdefinition, Applikation, das ist die Funktionsanwendung auf Argumente mit dem Ziel ein Resultat zu bestimmen, und Funktionskomposition.
Jeder Bezeichner in einem Kontext steht für genau einen Wert (wie in der Mathematik), Variablen existieren hier nicht.
In der funktionalen Programmierung werden mit Funktionen Algorithmen formuliert und das Interesse ist hierbei auf die Berechnung von Funktionswerten gerichtet.

2.2. Funktionsdefinition/-applikation

Eine Funktionsdefinition kann konkret oder anonym erfolgen.

Formell besteht eine konkrete Funktionsdefinition aus dem Definitionszeichen '=', einer linken Seite, die den Namen der Funktion und (wenn zur Definition nötig) formalen Parametern besteht, einer rechten Seite, die (evtl. unter Benutzung der formalen Parameter) einen Ausdruck entsprechenden Typs ist.

Beispiel: (Funktionsdefinition)
square 5 = 5*5
square (2+4) = (2+4)*(2+4)

 Die Definition begleitend ist die Typdeklaration, welche Auskunft darüber gibt, für welchen Typ die Funktion definiert ist.

Beispiel: (einfache Funktionsdefinition)
square :: Int -> Int
square n = n*n
 Die erste Zeile der Definition drückt durch -> aus, dass square eine Funktion ist, welche ein Argument vom Typ Int besitzt und welche ein Resultat vom Typ Int liefert.
Die zweite Zeile liefert die Definition der Funktion. Die Gleichung besagt, dass wenn square auf eine Variable/Ausdruck n angewendet wird, das Ergebnis n*n sein soll.

Beispiel: (Funktionsdefinition f. Funktion höherer Ordnung)
twice f x = f ( f x )
 Dabei ist f eine Funktion, die zweifach auf das Argument x angewandt wird.


Beispiel: (Funktionsanwendung)
square 2 -> 4
twice square 2 -> 2^4
 Die Ausführung eines funktionalen Programms erfolgt, in dem ein Ausdruck ausgewertet wird und einen Wert liefert.
In einer Funktionsdefinition kann auch eine Funktion auf eine weitere Funktion angewendet werden.

2.3. Lambda-Kalkül

Bei der Beschreibung von Programmiersprachen spricht man von zwei abstrakten Modellen. Imperativen Sprachen werden durch das Modell der Turingmaschine beschrieben. Das bedeutet, dass sie aus einer Folge von Befehlen bestehen, welche streng einer nach dem anderen hintereinander ausgeführt werden.
Das Lambda Kalkül hingegen bietet eine Abstraktion funktionaler Sprachen, es wird dazu benutzt, um eine Funktionsdefinitions zu Abstrahieren.
\x -> A
ist die allgemeine Form, welche eine (anonyme) Funktion definiert, die ein x bekommt und einen Ausdruck A als Funktionskörper hat.
Als Bausteine für das Lambda-Kalkül gibt es nur Funktionsdefinition und Funktionsabstraktion, keine Zahlen, Funktionsnamen, arithmetische Funktionen, Wahrheitswerte.
Alle Berechnungen werden auf die Definition von Funktionen und deren Anwendung zurückgeführt.
Diese Art der Funktionsdefinition wird benutzt, wenn die Funktion ohne eigenen Bezeichner verwendet werden soll. Dies bedeutet, dass die Funktion nur aus einer Funktion heraus aufgerufen werden kann, sie kann ohne Funktionsbezeichner nicht alleine appliziert werden.

Beispiel: Funktionsdefinition
\x -> x^2                       (definiert die Quadratfunktion)

Beispiel: Anwendung einer anonymen Funktion
(\x -> x^2) 2 -> 4		(anonyme Funktion)
twice (\x -> x^2)

Prinzipiell werden auch konstante Werte z.B. Zahlen als Funktionen definiert, in der Form Nachfolger(Nachfolger(Start)).
In den funktionalen Sprachen werden sie jedoch vordefiniert, so dass man nicht mit komplizierten Funktionsdefinitionen hantieren muss.

Beispiel: Definition der Wahrheitswerte und if-then
\x y -> x			(Projektion auf das 1.Argument -> true)
\y x -> y			(Projektion auf das 2.Argument ->false)
\b x y -> b x y 	        (b ist entweder true oder false)

Ohne Variablen und arithmetischen Ausdrücken existiert natürlich auch keine Iteration. Alle Probleme werden über Funktionen und Rekursion gelöst. Bemerkenswert ist hierbei, dass keine festen Typen zugewiesen werden, Lambda-Ausdrücke sind untypisiert. Eine Funktion kann daher auf Zahlen, Zeichenfolgen oder Funktionen angewendet werden, ohne sie umzuschreiben. Auf diese Weise kann ein Sortieralgorithmus geschrieben werden, der ohne Veränderung, auf Zahlen, Zeichenfolgen, Listen u.a. angewendet werden kann.

2.4. Funktionskomposition

In der Mathematik gibt es den Ausdruck g°f, was bedeutet, dass erst f angewendet wird, dann darauf g anzuwenden ist. Es werden zwei Verarbeitungsschritte nacheinander durchgeführt:



Eine Funktion transformiert einen oder mehreren Input in einen Rückgabewert (Output). Wird der Rückgabewert einer Funktion als Input für eine andere Funktion verwendet so wird dies als Funktionskomposition verwendet.
In Haskell-Schreibweise:

g.f Der '.' in der Definition ist ein Operator, der die Funktionen verkettet. Der Rückgabewert von f wird zum Input von g. Diese Kette kann beliebig fortgesetzt werden. Der Rückgabewert kann auch eine Funktion sein, wenn es sich um Funktionen höherer Ordnung handelt.

Definiert ist der '.'-Operator wie folgt:



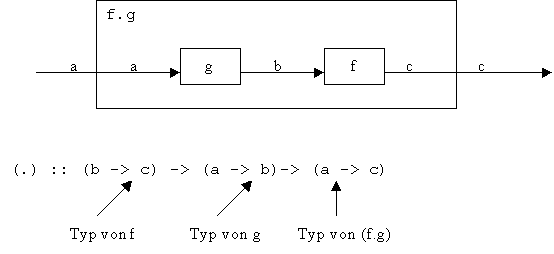
(g.f) x = g(f x)

Beispiele:
(+3).(+5) = (+8)
length = sum.map(\x ->1)
Durch die Funktionskomposition können beliebig viele neue Funktionen einfach erzeugt werden.
Es muss nur gelten:
Wertebereich von f muss zu Argumentbereich von passen!

Beispiel: (2.Ableitung)
(diff.diff) cos 0
-1.07288

Vorsicht:
diff.diff cos 0 wird aufgefasst als diff.((diff cos) 0 ) wegen höchster Priorität der Funktionsapplikation!
Funktionsapplikation (bei higher order functions) und Funktionskomposition dürfen nicht verwechselt werden!


Die Komposition von Funktion und inverser Funktion gibt Identität!

2.5. Kombinatoren

Kombinatoren sind Funktionen, die das Prinzip der Komposition nutzen um aus einfachen Funktionen komplexe Funktionen zu konstruieren. twice f = (f.f)
twice wendet eine beliebige Funktion mit einem Argument auf das Argument zweimal an.

Beispiel durch Reduktion:
(twice succ) 12
~>(succ.succ) 12
~> succ (succ 12)
~> succ 13
~> 14

2.6. Funktionen höherer Ordnung

Funktionen höherer Ordnung sind Funktionen die als Argumente Funktionen aufnehmen können und als Rückgabewert eine Funktion zurückliefern können.
Ein Beispiel für eine Funktion höherer Ordnung sind Kombinatoren, da ein Kombinator eine Funktion ist, die als Ergebnis eine Funktion zurückliefert.

Beispiel:
twice :: (a -> a) -> (a -> a)
[ XML und Haskell Seminar ] ... [ Thema XML Verarbeitung mit Haskell ] ... [ 3. XML-Verarbeitung ]