Inhalt | Einführung | Theorie | JavaCC | JavaCC in der Praxis

Theorie

Parser

Um zu verstehen, wie JavaCC arbeitet, müssen wir zunächst einmal erläutern, was für generelle Anforderungen an einen Parser gestellt werden. Ein Parser hat die Aufgabe, eine beliebige Eingabe in seine Bestandteile zu zerlegen und diese in ein neues Format zu überführen. Mit Format ist üblicherweise eine geeignete Datenstruktur gemeint, die in der Lage ist, die Informationen zu tragen. Klassisches Beispiel für eine solche Datenstruktur ist die Baumstruktur, die neben den eigentlichen Informationen eine Hierarchie erstellt. Die verarbeitung von HTML Dokumenten soll hier als klassisches Beispiel dienen, anhand dessen man den grundsätzlichen Ablauf eines Parsers demonstrieren kann. HTML-Dokumente sind zunächst einmal nichts anderes als Textdokumente, die an einen Browser geschickt werden können. Soll der Browser das HTML-Dokument darstellen, so muss der HTML-Parser zunächst alle HTML-Elemente erkennen und in eine neue Datenstruktur überführen. Im Fall von HTML bietet sich eine Baumstruktur an, da anhand der Anordnung innerhalb des Quelltextes eine Hierarchie abgeleitet werden kann. Der so gewonnene Baum kann nun beliebig weiterverarbeitet werden. Beispielsweise könnnen mittels Javascript Manipulationen vorgenommen werden, oder aber es erfolgt eine grafische Ausgabe über den Browser. Ein weiteres Beispiel, in dem eine andere Datenstruktur zum Einsatz kommen könnte, ist die URL, die ebenfalls in ihre einzelnen Bestandteile zerlegt werden muss, ehe eine DNS-Anfrage gestartet werden kann.

Die eben vereinfacht geschilderten Vorgänge gliedern sich grundsätzlich in zwei Teilaufgaben

Lexikalische Analyse

Die lexikalische Analyse hat die Teilaufabe, eine Eingabe in eine Folge von logisch zusammengehörigen Einheiten, den sogennanten Token, zu zerlegen. Progamme, die eine solche lexikalische Analyse durchführen, bezeichnet man auch als Lexer. Die Token bilden atomare Bausteine, aus denen sich letztendlich die Eingabe zusammensetzt. Sie sind konstante Bezeichner, die eine eindeutige Identifikation einzelner Symbole ermöglichen. Folgendes Beispiel demonstriert die Funktionsweise eines Lexers.

Gegeben sei folgendes C-Programm

int main() {
  return 0;
}
Möchte man das kurze C-Progamm übersetzen, so muss unter anderem die Syntax geprüft werden. Ein entsprechender Parser würde folgende Symbole erkennen: 
'int'   '_'   'main'   '('   ')'   '_'   '{'   '\n'
'\t'   'return'   '_'   '0'   ';'   '\n'
'}'   '\n'
Wie bereits erwähnt, kann man Symbole zu Token zusammenfassen. Beispielsweise interessiert es nicht, um was für einen konkreten Rückgabewert es sich handelt. Entscheidend ist, aus syntaktischen Gesichtspunkten, allein der Rückgabetyp. Solche Typen definiert man mittels regulärer Ausdrücke. So kann man relativ einfach festlegen, was unter einer Zahl verstanden werden soll, oder wie Variablen auszusehen haben. Im Folgenden ist das Programm von oben in die einzelnen Token aufgeteilt. 
KWINT, SPACE, ID, OPAR, CPAR, SPACE, OBRACE, SPACE,
SPACE, KWRETURN, SPACE, OCTALCONST, SPACE, SEMICOLON, SPACE,
CBRACE, SPACE, EOF

Ein Token kann somit als Tupel gesehen werden, dass neben den Bezeichner eine Ausprägung beinhaltet

Syntaktische Analyse

Die syntaktische Analyse ist die zweite wesentliche Aufgabe, die ein Parser zu leisten hat. Hier geht es darum, die Form und den Aufbau einer Sprache zu analysieren und zu entscheiden, ob diese den Spezifikationen genügt. Dies ist besonders wichtig, da so sichergestellt werden kann, dass die Sprache verarbeitet werden kann. Grundlage für eine syntaktische Analyse ist immer eine Grammatik die festlegt, wie die Sprache aufgebaut ist. Zu einer Grammatik gibt es viele mögliche Eingaben, die einer Grammatik genügen. Die Gesamtheit der Eingaben bildet die Sprache. Das folgende Beispiel zeigt eine kurze Grammatik sowie eine Eingabe und den dazugehörenden Syntaxbaum.

Beispiel:

A -> B | A + A | A x A | (A)
B -> a | b | Ba | Bb | B0 | B1

Eingabe:

(a0 + b1) x a + b

Ein Syntaxbaum

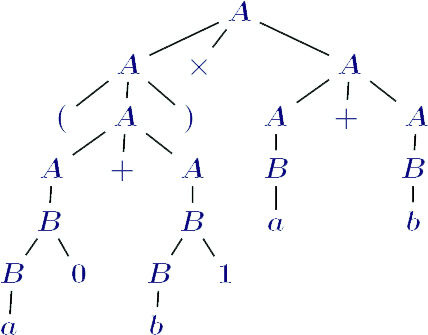
An diesem Beispiel lässt sich des weiteren das Top Down - Verfahren erläutern. Bei diesem Verfahren wird, ausgehend von einem Wurzelknoten, der gesamte Baum aufgebaut.

Backus-Naur-Form

Die Backus-Naur-Form kurz BNF ist eine formale Metasprache, die zur Darstellung kontextfreier Grammatiken genutzt werden kann. Es bietet sich daher an, mittels ihrer Hilfe Grammatiken zu formulieren. Da sich in dieser Notation vorliegende Grammatiken einfach in JavaCC übernehmen lassen, soll an dieser Stelle kurz auf diese Darstellungsform eingegangen werden.

Die BNF unterscheidet zwei Arten von Zeichen. Terminal- und Nichtterminalsymbole, auch syntaktische Variable genannt. Terminalsymbole bestehen aus Zeichen und zeichnen sich dadurch aus, dass diese atomar, d.h. nicht weiter zerlegbar sind. Nichtterminalsymbole, eingeschlossen in spitzen Klammern, werden in Ableitungsregeln (Produktionen) definiert und solange abgeleitet, bis sie durch Terminalsymbole ersetzt worden sind. Die Zeichenfolge ::= wird zur Definition verwendet, das Zeichen | dient als Alternative.

Beispiel:

<ziffer> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Eine Ziffer (Nichtterminalsymbol) kann durch eines der Terminalsymbole (0-9) dargestellt werden

Sequenz:

<zahl >  ::= <zahl> | <ziffer>
<ziffer> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Durch die hier enthaltene Rekursion lässt sich eine beliebigstellige Zahl darstellen