Typklassen in Haskell
Übersicht
Grundlagen
Es gibt drei Arten von Integern: positive, Null und negative Integer. Daher könnte Integer durch folgenden Datentypen
deklariert werden:
data Integer = Neg Positive | Zero | Pos Positive
data Positive = One | Succ Positive
|
Der Typ
Positive liefert die positiven natürlichen Zahlen, der Typ
Integer eine vorzeichenbehaftete positive
Zahl oder Null. Da jetzt der Typ
Integer deklariert ist, können nun die rationalen Zahlen als Paare von Integern
(s. Beispiel. Rational)
und die komplexen rationalen Zahlen als Paare von rationalen Zahlen dargestellt werden.
Ebenso können passende Approximationen der reellen Zahlen als Sequenz von Dezimalzahlen konstruiert werden. Die Schlussfolgerung ist,
dass die gesamte Arithmetik definiert werden kann, ohne mehr als einfache symbolische Rechenwege benutzen zu müssen.
Grundsätzlich soll klargestellt werden, dass alle arithmetischen Berechnungen dargestellt werden können.
Jeder Computer besitzt eine fest implementierte Arithmetik-Einheit, die zumindest einfache Integer-Arithmetik beherrscht. In vielen
Maschinen gibt es ebenso eine feste Implementierung für den Umgang mit Fliesskommazahlen. Ist das nicht der Fall, so kann die
Fliesskomma-Arithmetik effizient durch maschinennahe Software implementiert werden. Es ist effizienter, diese Einheiten zu nutzen, als
sich auf die symbolischen Alternativen zu verlassen.
In den verschiedenen Programmiersprachen wird unterschiedlich mit Zahlen umgegangen.
Haskell kennt unter anderem folgende Typen:
- Int sind ganze Zahlen mit beschränkter Genauigkeit (32 bit).
- Integer sind ganze Zahlen mit unbeschränkter Genauigkeit.
- Float sind Fliesskommazahlen mit einfacher Genauigkeit.
- Double sind Fliesskommazahlen mit doppelter Genauigkeit.
Es gibt weitere Typen in Haskell, inkl. des Typs Rational und Complex, die hier aber nicht benutzt werden sollen
(im folgenden Abschnitt wird ein Weg gezeigt, rationale Zahlen zu definieren). Es wird auch nicht genau gesagt, was einfache und doppelte
Genauigkeit bedeuten. Die Bedeutung differiert in Abhängigkeit von der vorhandenen Hardware, auch wenn es einen Standard gibt,
dem die meisten Rechner entsprechen.
Arithmetik mit Int ist am schnellsten; Arithmetik mit Integer ist erheblich langsamer.
Andererseits ist die Integer-Arithmetik exakt, die Int-Arithmetik nicht.
Ausserhalb einer bestimmten Spannweite kommt es zu Integer-Overflow.
Der Computer gibt entweder eine Fehlermeldung oder schlicht falsche Resultate zurück. Es muss allerdings beachtet werden, dass es
den Datentypen Nat für natürliche Zahlen in Haskell nicht gibt. Trotzdem ist der Geist der natürlichen Zahlen in den
Integern präsent, weil weiterhin Pattern-Matching benutzt werden kann. Beispielsweise kann definiert werden:
fact :: Integer -> Integer
fact 0 = 1
fact(n + 1) = (n + 1) * fact n
|
Dies spiegelt die vorhin gezeigte rekursive Definition wieder, als geschrieben wurde Zero statt 0 und Succ n statt
n + 1. Pattern-Matching mit Integern ist auf die Unterklasse der natürlichen Zahlen beschränkt. Folglich passt das
Muster (n + 1) nur auf positive Integer. Auch wenn Pattern-Matching durch den Gebrauch der Fallunterscheidung vermieden werden
kann (oder besser durch Benutzung einer neuen Version von foldn), gibt es viele Beispiele, wo "pattern matching" die klarste
Methode der Definition ist. Zusätzlich parallelisiert der Gebrauch von Pattern-Matching die Fälle in einem
Induktions-Nachweis.
Es gibt einen entscheidenden Unterschied zwischen dem Konstruktor Succ aus Nat und der Funktion (+1)
auf Integern. Während Succ eine nicht-strikte Funktion ist, ist (+1) strikt. Also gibt es keine partiellen Zahlen in der
implementierten Arithmetik.
[nach oben]
Numerische Typklassen
Die gleichen Symbole +, *, usw., werden in jedem numerischen Typ für Arithmetik benutzt, auch wenn diese Operatoren verschiedene
Operationen auf verschiedenen Typen bedeuten. Mit anderen Worten: +, *, usw. sind überladene Funktionen wie == und <. Haskell
benutzt ein hochentwickeltes System von Typklassen, um die unterschiedlichen Zahltypen zu beschreiben. Stattdessen wird hier ein vereinfachtes
Schema beschrieben, das die grundlegenden Ideen verdeutlichen soll. Alle Zahlentypen in Haskell sind Instanzen der Typklasse Num,
definiert durch:
class (Eq α, Show α) => Num α where
(+),(-),(*) :: α -> α -> α
negate :: α -> α
fromInteger :: Integer -> α
x - y = x + negate y
|
Die Klasse Num stellt eine Default-Definition von (-) zur Verfügung und zwar durch negate. Alle Zahlen können
auf Gleichheit getestet werden und haben eine druckbare Darstellung. Alle Zahlen können addiert, subtrahiert und multipliziert
werden. Schliesslich gibt es noch ein Umformungsfunktion fromInteger, um mit Konstanten zu arbeiten. Eine Integer-Konstante, wie
z.B. 3 oder 65472233, stellt die Anwendung von fromInteger auf den entsprechenden Integerwert dar. Also:
Durch diese indirekte Definition können numerische Integer-Konstanten als Werte jedes passenden numerischen Typs interpretiert werden.
Nicht alle Zahlen können mit < verglichen werden, komplexe Zahlen z.B. nicht. Die Typklasse
Real umfasst alle Arten von
berechenbaren Zahlen, für die < eine sinnvolle Operation darstellt:
class (Num α, Ord α) => Real α where
toRational :: α -> Rational
|
Der Typ Rational besteht aus Paaren von Integerzahlen und wird später behandelt. Die neue Funktion toRational verkörpert die Idee,
dass jede finite-precision Real-Zahl als Verhältnis von zwei arbitrary-precision Integern ausgedrückt werden kann. Als letzte Typklassen
werden Integral und Fractional erwähnt. Die Typklasse Integral ist definiert durch:
class (Real α, Enum α) => Integral α where
(div),(mod) :: α -> α -> α
toInteger :: α -> Integer
|
Die Bestandteile von
Integral sind die zwei primitiven Typen
Int und
Integer. Für jeden Typen sind die Operatoren
div und
mod als Primitiven definiert. Wenn
x und
y Integer sind und
y ist nicht 0, dann gilt:
x div y = 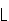 x/y
x/y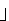
, wobei
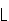 x
x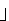
(gesprochen als 'Floor' von
x) der grösste Integer
n ist,
der die Gleichung n ≤ x erfüllt.
Beispiel: 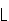
13.8
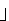
= 13 und
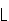
-13.8
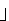
= -14.
Die Berechnung von
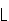 x
x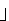
wird im
Abschnitt
Lineare Suche weiter bearbeitet.
Der Wert
x mod y wird
definiert durch die Gleichung:
x = (x div y) * y + (x mod y)
|
Die Zahl y in (x mod y) wird als Modulus bezeichnet. In den meisten Anwendungen ist der Modulus positiv.
Für positive y gilt 0 ≤ x mod y < y. Tatsächlich sind für positive y die Werte x div y
und x mod y die einzigen Integer q und r, die die Bedingungen erfüllen:
x = q * y + r und 0 ≤ r < y
|
Wenn y negativ ist, dann gilt y < x mod y ≤ 0.
Die Typklasse
Fractional umfasst die Arten von Zahlen, für die eine Division sinnvoll ist, und beinhaltet die Fliesskommzahltypen
Float und
Double.
Beispiel:
class (Num α) => Fractional α where
(/) :: α -> α -> α
fromRational :: Rational -> α
|
Die Umwandlungsfunktion fromRational wird für Fliesskommakonstanten benutzt. Eine Konstante, wie 2.1414 (= pi), steht für die
Anwendung von fromRational auf den entsprechenden Wert des Typen Rational. Also:
2.1414 :: Fractional α => α
|
Fliesskommakonstanten werden auf diese indirekte Art definiert, damit sie als Werte passender numerischer Typen interpretiert werden können.
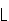 x/y
x/y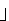 , wobei
, wobei
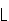 x
x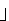 (gesprochen als 'Floor' von x) der grösste Integer n ist,
der die Gleichung n ≤ x erfüllt. Beispiel:
(gesprochen als 'Floor' von x) der grösste Integer n ist,
der die Gleichung n ≤ x erfüllt. Beispiel: 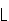 13.8
13.8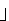 = 13 und
= 13 und
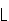 -13.8
-13.8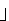 = -14. Die Berechnung von
= -14. Die Berechnung von 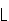 x
x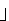 wird im
Abschnitt Lineare Suche weiter bearbeitet. Der Wert x mod y wird
definiert durch die Gleichung:
wird im
Abschnitt Lineare Suche weiter bearbeitet. Der Wert x mod y wird
definiert durch die Gleichung: