Beispiel: Lineare und binäre Suche
Übersicht:
Lineare Suche:
Die Funktion
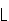
-
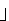
bekommt eine unbeschränkt-genaue (arbitrary) Realzahl und liefert einen
Integer zurück. Sie ist primitiver als
div, kann aber nicht in Haskell implementiert werden, weil dieses nur beschränkt-genaue
Realzahlen darstellen kann.
Nichtsdestotrotz ist es lehrreich zu sehen, wie
floor :: Float -> Integer programmiert werden kann. Das Problem ist nicht so trivial, wie
es scheint, daher wird das Programm systematisch entwickelt. Es werden zwei Programme entwickelt werden, von denen eins wesentlich effizienter ist
als das andere. Die Strategien hinter diesen Programmen heissen lineare und binäre Suche. Der Abschnitt endet mit einer zweiten Anwendung zur
Berechnung von Wurzeln.
Zunächst die Spezifikation:
floor :: Float -> Integer
floor x = n ≡ n ≤ x < n + 1
|
Während man darüber nachdenkt, welche Gestalt das Programm für floor annehmen wird, ist es verführerisch, sofort mit einer
Fallanalyse zu beginnen. Es wird überlegt was zu tun ist, wenn x positiv, negativ oder möglicherweise 0 ist. Aber die
Spezifikation erwähnt keine Fälle und es wird auch keine Fallanalyse verwendet. Programme, die Fallanalysen vermeiden, sind klarer und
einfacher.
Gesucht wird n und die Spezifikation suggeriert mindestens einen Weg, um die Suche durchzuführen: Gesucht wird ein n,
für das gilt n ≤ x und das so lange erhöht wird, bis die Bedingung x < n + 1 ebenfalls erfüllt ist. Es kann
natürlich auch ein n gesucht werden, das die Bedingung x < n + 1 erfüllt, um dann n so lange zu verkleinern, bis
die Bedingung n ≤ x auch gilt. Der Gedanke, so lange zu suchen, bis eine Bedingung erfüllt wird, kann in einer Funktion
until gekapselt werden:
until :: (α -> Bool) -> (α -> α) -> α -> α
until p f x = if p x then x else until p f (f x)
|
Die Suche nach einem n, das die Bedingung n ≤ x erfüllt und wo x eine fixe Zahl ist, kann mit einem beliebigen Integer
beginnen, der dann so lange dekrementiert wird, bis die Bedingung erfüllt ist. Z.B. die Suche:
lower :: Integer -> Integer
lower = until (≤ x) decrease, where decrease n = n - 1
|
löst die Aufgabe,
wenn sie auf einen beliebigen Startwert angewendet wird. Die Suche wird terminieren, weil für jedes Real x ein Integer n
existiert, für das gilt n ≤ x. Der in der ersten Suche gefundene Integer n kann erheblich zu klein sein, so dass in einer zweiten
Suche n solange erhöht werden muss, bis die Bedingung x < n + 1 erfüllt ist. n muss in Schritten von 1 erhöht
werden, um die Bedingung n ≤ x zu behalten. Die zweite Suche kann auf zwei Arten beschrieben werden. Entweder als
until (> (x - 1)) increase where increase n = n + 1
|
oder als decrease · upper
upper = until (> x) increase where increase n = n + 1
|
In der zweiten Lösung ist upper das Gegenteil zu lower. Die Funktion decrease · upper
wird auf das Ergebnis der ersten Suche angewendet. Das komplette Programm sieht wie folgt aus:
floor :: Float -> Integer
floor x = searchFrom 0
where searchFrom = decrease · upper · lower
lower = until(≤ x) decrease
upper = until(> x) increase
decrease n = n - 1
increase n = n + 1
|
Es wurde versucht, dieses Programm so klar wie möglich darzustellen. Die Namen searchFrom, increase (anstelle des äquivalenten
Succ) und decrease anstelle von pred wurden ausgewählt, um den Beitrag dieser Teile zur Definition zu verdeutlichen und die
Funktionen lower und upper so gegensätzlich wie möglich darzustellen. Zuletzt wurden die unterschiedlichen Hilfsfunktionen
lokal zur Hauptdefinition erstellt. Das Programm ist überraschend kurz, was hauptsächlich auf das Fehlen einer Fallanalyse bzgl. des
Vorzeichens von x zurückzuführen ist. Man kann einfach sehen, wie beide Fälle behandelt werden: Wenn 0 ≤ x, dann terminiert
die erste Schleife sofort, während die zweite die eigentliche Arbeit macht. Ist x < 0, ist es genau andersherum.
[nach oben]
Binäre Suche:
Das obige Programm ist nicht wirklich effizient, weil es ungefähr abs x Schritte braucht, um das Resultat zu finden. Ein effizienterer
Weg ist es, zuerst zwei Integer m und n zu finden, sodass m ≤ x < n, um dann m und n
näher zusammen zu bringen, sodass schliesslich die Bedingung m + 1 = n erfüllt ist. Das Entkoppeln der zwei Suchen ist
deshalb vorteilhaft, weil grössere Schritte benutzt werden können. Genauer gesagt, ist beispielsweise das Suchpaar zu betrachten:
lower = until(≤ x) double
upper = until(> x) double
|
mit double n = 2 * n. Unter der Voraussetzung, dass lower auf eine negative Zahl angewendet wird und upper auf eine positive, ist
garantiert, dass die zwei Suchen ein Paar (m,n) mit m ≤ x < n finden, wobei die Anzahl der Schritte proportional ist zu
log2 (abs x). Beide Suchen müssen durch eine dritte Suche ergänzt werden, die das Paar (m,n) näher zusammenbringt, bis
m + 1 = n gilt. Entweder wird m in Schritten von 1 inkrementiert oder andersrum n in Schritten von 1 dekrementiert. Eine bessere
Lösung betrachtet den Integer p = (m + n) div 2 als Mittelwert zwischen m und n. Daraus folgt, wenn
m + 1 < n, dann ist m < p < n. Ist p ≤ x, kann m auf den Wert von p erhöht werden. Ist x < p,
kann n auf p verringert werden. Daraus ergibt sich folgendes Programm:
floor x = searchFrom (-1,1)
where searchFrom = fst · middle · cross(lower, upper)
lower = until(≤ x) double
upper = until(> x) double
middle = until done improve
done(m, n) = (m + 1 = n)
improve(m, n) = if p ≤ x then (p, n) else (m, p)
where p = (m + n) div 2
|
Die Funktion cross wurde bereits definiert. Das neue Programm benötigt eine Anzahl von Schritten, die proportional ist zu
log2 (abs x). Z.B. mit x = 17,3 ergibt sich lower (-1) = -1 und upper 1 = 32. Die dritte Suche erzeugt die
Zwischenwerte:
(-1,32) -> (15,32) -> (15,23) -> (15,19) -> (17,19) -> (17,18)
|
und gibt 17 zurück. Mit x = -17,3 ist lower (-1) = -32 und upper 1 = 1. Die dritte Suche erzeugt die Zwischenwerte:
(-32,1) -> (-32,-16) -> (-24,-16) -> (-20,-16) -> (-18,-16) -> (-18,-17)
|
und gibt -18 zurück. Die Strategie hinter diesem Programm wird als binäre Suche bezeichnet. Anstatt zwei Integer in Schritten von 1
zusammen zu bringen, kann man den Abstand manchmal auf die Hälfte zusammenkürzen.
[nach oben]
Beispiel: Berechnung von Quadratwurzeln
In einem zweiten Beispiel für die Suche soll eine Definition für die Funktion sqrt erstellt werden, um die
(nicht negative) Quadratwurzel einer nichtnegativen Zahl zu berechnen. Die mathematische Spezifikation von sqrt ist, das gilt:
sqrt x ≥ 0 und square(sqrt x) = x
|
wenn x ≥ 0. Diese Spezifikation ist streng, weil sie keine limited-precision für arithmetische Operationen auf aktuellen Computern
zulässt. Sie verlangt beispielsweise, dass:
exakt berechnet wird. Wie in Kapitel 4 und 9 gezeigt werden wird, ist es durchaus möglich, eine Funktion zu entwerfen, die eine unendliche Liste
von Ziffern zurück gibt, auch wenn der Prozess des Druckens dieser Liste niemals terminiert. Der Programmierer kann dann zeigen, dass sqrt
seine Spezifikation erfüllt, indem er nachweist, dass die Liste von Ziffern bis zum verlangten Genauigkeitsgrad approximiert, wenn sie nur lange
genug fortgeführt wird. Für dieses Beispiel jedoch wird die Spezifikation dahingehend abgeschwächt, dass srqt :: Float -> Float
sqrt x ≥ 0 und abs(square(sqrt x) - x < eps
|
erüllt für ein infinitisimal kleines eps > 0. Um die geänderte Spezifikation zu verdeutlichen, soll eps = 0.0001
und x = 2 sein. Gefordert ist:
abs(square(sqrt 2) - 2) < 0.0001
|
und aus
1.4141 * 1.4141 = 1.99967881
1.4142 * 1.4142 = 1.99996164
1.4143 * 1.4143 = 2.00024449
|
folgt, dass der Wert sqrt 2 = 1.4142 eine akzeptable Antwort darstellt.
Um sqrt zu konstruieren, wird das Newton´sche Näherungsverfahren zum Finden der Wurzeln einer gegebenen Funktion angewendet.
Dabei handelt es sich um eine iterative Methode, die wiederholt die Approximation der Lösung verbessert, bis der geforderte
Genauigkeitsgrad erreicht ist. Im Falle der Quadratwurzeln sagt Newtons Methode, dass wenn yn eine Näherung zur √
x, dann ist:
die bessere Näherung. In einem Beispiel mit x = 2 und y0 = x ist:
y0 = 2
y1 = (2 + 2/2)/2 = 1.5
y2 = (1.5 + 2/1.5)/2 = 1.4167
y3 = (1.4167 + 2/1.4167) = 1.4142157
|
Durch Iteration dieses Prozesses kann Wurzel 2 bis zu jedem beliebigen Genauigkeitsgrad berechnet werden, eingeschränkt nur durch die
Begrenzungen der Computer-Arithmetik. Durch die Benutzung der bereits vorgestellten Funktion until kann sqrt mit folgendem
Programm implementiert werden:
sqrt :: Float -> Float
sqrt x = until done improve x
where done y = abs(y * y -x) < eps
improve y = (y + x/y)/2
|
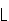 -
-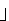 bekommt eine unbeschränkt-genaue (arbitrary) Realzahl und liefert einen
Integer zurück. Sie ist primitiver als div, kann aber nicht in Haskell implementiert werden, weil dieses nur beschränkt-genaue
Realzahlen darstellen kann.
Nichtsdestotrotz ist es lehrreich zu sehen, wie floor :: Float -> Integer programmiert werden kann. Das Problem ist nicht so trivial, wie
es scheint, daher wird das Programm systematisch entwickelt. Es werden zwei Programme entwickelt werden, von denen eins wesentlich effizienter ist
als das andere. Die Strategien hinter diesen Programmen heissen lineare und binäre Suche. Der Abschnitt endet mit einer zweiten Anwendung zur
Berechnung von Wurzeln.
bekommt eine unbeschränkt-genaue (arbitrary) Realzahl und liefert einen
Integer zurück. Sie ist primitiver als div, kann aber nicht in Haskell implementiert werden, weil dieses nur beschränkt-genaue
Realzahlen darstellen kann.
Nichtsdestotrotz ist es lehrreich zu sehen, wie floor :: Float -> Integer programmiert werden kann. Das Problem ist nicht so trivial, wie
es scheint, daher wird das Programm systematisch entwickelt. Es werden zwei Programme entwickelt werden, von denen eins wesentlich effizienter ist
als das andere. Die Strategien hinter diesen Programmen heissen lineare und binäre Suche. Der Abschnitt endet mit einer zweiten Anwendung zur
Berechnung von Wurzeln.