Metaprogrammierung mit Template Haskell

3 Template Haskell

Der Aufbau der Template Haskell Bibliothek wird anhand einer 3-Layer-Architektur verdeutlicht, die in der unten stehenden Abbildung 1 ersichtlich ist.

Abbildung 1 Template Haskell 3-Schichten Architektur

Das Fundament dieser Architektur stellen die Abstrakten Datentypen dar, in welche der Programmcode transformiert wird. Dieser Layer enthält alle benötigten Konstruktorfunktionen und kann somit eigenständig verwendet werden. Die Q-Monade kann als eine Art "intelligente" Zugriffsschnittstelle auf dieses Datentypen-Fundament gesehen werden.

Um das Arbeiten mit der Q-Monade zu vereinfachen, bietet der zweite Layer mit den sog. Syntax-Konstruktionsfunktionen für jeden "einfachen" Konstruktor aus Layer 1 eine monadische Variante an.

Der oberste Layer der Schichtenarchitektur bildet schließlich das Quasi-Quoting, mithilfe dessen es möglich ist, viele der abstrakten Datentypen unter Verwendung einer eigenen, domain-spezifischen Syntax zu konstruieren. Damit dient dieser Layer in erster Linie dem Entwickler als komfortable Zugriffsschnittstelle auf Layer 1. Das Quasi-Quoting verwendet zum Zugriff auf den Layer 1 die Q-Monade.

Zur Erstellung der Templates können die drei Ebenen beliebig vermischt werden, da die oberen beiden Layer nur Zugriffsschnittstellen für den Layer 1 darstellen. Im Folgenden wird der Aufbau der Bibliothek von unten nach oben näher betrachtet, um die eben kurz angerissenen Zusammenhänge zwischen den Layern zu verdeutlichen.

3.1 Programmcode als Abstrakte Datentypen

Zur Darstellung von Haskell Code bzw. des Syntaxbaums, werden einfache Abstrakte Datentypen verwendet. So existieren im untersten Layer 1 Datentypen und Konstruktoren für Ausdrücke (Exp), Patterns (Pat), Deklarationen (Dec) und Typen (Typ) etc. Da es sich um einfache abstrakte Datentypen handelt, können diese mit den gewohnten Analyse- und Destructuring-Methoden wie case -Anweisungen und Pattern Matching verarbeitet werden.¹⁴

Will man bspw. einen Tupel-Ausdruck erzeugen, so findet sich dafür der Konstruktor TupE in der Bibliothek. Wie man an diesem Beispiel sieht, ist die Namensgebung der Konstruktorfunktionen intuitiv. Will man bspw. eine Lambda-Funktion konstruieren, so heißt der Konstruktor LamE. Desweiteren fällt auf, dass die Namen der Konstruktoren einer Namenskonvention nach mit folgenden Suffixen enden:

E für Ausdrücke
P für Patterns
D für Deklarationen
T für Typdefinitionen

Diese Suffixe geben eine Art Kontext an, oder besser gesagt Gültigkeitsbereich, innerhalb dessen der Konstruktor verwendet werden darf. Dies bedeutet, dass bei der Erzeugung eines Tupels der Kontext berücksichtig werden muss; ein Tupel ist nicht gleich ein Tupel. So wird der Konstruktor TupP verwendet, um ein Tupel innerhalb eines Patterns anzugeben, TupE hingegen, um ein Tupel als Ausdruck zu kennzeichnen. Der Kontextbezug der Konstruktoren hat damit den Vorteil, dass er verhindert, dass Kontexte vermischt werden und Konstruktoren dadurch in Kontexten auftreten, wo sie nicht hingehören. So ist es z.B. nicht möglich, Lamda-Funkionen innerhalb eines Patterns zu erstellen, da es nur einen LamE-Konstruktor gibt.

In dem folgenden Beispiel wird eine Lambda-Funktion zum Abbilden der Identität eines Tupels konstruiert, um den eben vorgestellten Sachverhalt noch einmal zu verdeutlichen.

```
LamE [ TupP [ VarP $ mkName "x", 
```
```
              VarP $ mkName "y" ] 
```
```
     ] 
```
```
     ( TupE [ VarE $ mkName "x", 
```
```
              VarE $ mkName "y"]
```
```
     )
```

Aus der Typsignatur des Konstruktors LamE :: [Pat] -> Exp -> Exp ist ersichtlich, dass dieser eine Liste von Patterns([Pat]) erwartet und einen Ausdruck vom Typ Exp, auf den die Pattern-Liste abgebildet wird. In dem obigen Beispiel wird als einziges Pattern-Element ein Tupel mit TupP :: [Pat] -> Pat erzeugt. Die einzelnen Tupel-Variablen werden dem Tupel also in Form einer Liste [Pat] übergeben. In diesem Fall heißen die beiden Tupel-Variablen x und y. Um diese in gültige Pattern-Variablen umzuwandeln, muss der Konstruktor VarP :: Name -> Pat verwendet werden. Dieser Konstruktor erwartet wiederum einen Parameter vom Typ Name. Der abstrakte Datentyp Name wird in Haskell zur Repräsentation von Namen verwendet. Um aus x und y einen Ausdruck vom Typ Name zu konstruieren, existiert die Funktion mkName :: String -> Name. Betrachtet man die Zuweisungsseite des Lambda-Ausdrucks, so stellt man fest, dass diese bis auf die Konstruktornamen (bezogen auf das Kontext-Suffix) identisch ist mit der Pattern-Seite.

3.1.1 Problem des Typchecks

Trotzdem der oben genannten Vorteile durch die Darstellung von Programm Code in Form von ADTs, führt eben diese Darstellungsform auch zu einigen Nachteilen. Die Konstruktion von Code-Fragmenten kann mitunter recht komplex und unübersichtlich werden. Weitaus problematischer ist allerdings die Tatsache, dass semantische Funktionalitäten wie Scoping und Typcheck nur unzureichend bis garnicht unterstützt werden.¹⁵ Deutlich wird dies bei der Betrachtung des folgenden Code-Ausschnitts:

InfixE (Just (LitE (IntegerL 1))) (VarE $ mkName "+") (Just (LitE (CharL 'a')))

Der oben abgebildetet Syntaxbaum entspricht dem Ausdruck 1 + 'a'. Da 'a' vom Typ Char ist und Char nicht die Klasse Num instanziert, sollte der Compiler eine entsprechende Fehlermeldung generieren - was er allerdings nicht tut. Der Grund dafür ist, dass die Ausdrücke durch Verwendung der Typkonstruktoren in die zugehörigen ADTs "eingewickelt" werden, wodurch neue Typen entstehen. Die 1 wird bspw. mit LitE (IntegerL 1) in ein Exp ungewandelt - ebenso die Funktion Num a => (+) :: a -> a -> a . Für den Compiler ist aus diesen ADTs nicht ersichtlich, dass es sich semantisch dabei um Haskell-Code handelt.

3.1.2 Problem des Scopings

Wie bereits erwähnt, weiß der Compiler anhand der ADTs nicht, dass es sich eigentlich um Haskell-Code handelt. Demzufolge weiß er auch nichts über die Scopes und die Bindings der eingewickelten Daten. Deutlich wird dies an dem folgenden Beispiel.

LamE [VarP mkName "x"](VarE mkName "notInScope")

Der oben definierte Lambda-Konstruktor kann nach der Umwandlungin Haskell-Code (dazu später mehr) nur dann vom Compiler übersetzt werden, wenn in dem zugehörigen Scope auch eine Funktion notInScope definiert ist. Andernfalls wird vom Compiler folgende Fehlermeldung generiert.

not in scope 'notInScope'

Ein weiteres Problem ergibt sich beim Zusammenführen von mehreren Meta-Funktionen. Die Tatsache, dass die den Konstrukoren übergebenen Namen "manuell" mithilfe der Funktion mkName angegeben werden, kann zu Namenskonflikten führen. Deutlich wird dies an dem folgenden Beispiel¹⁶:

```
cross :: Exp -> Exp -> Exp
```
```
cross f g
```

          = LamE [TupP [ VarP $ mkName "x",

                         VarP $ mkName "y"

```
                       ]
```
```
                 ] $
```

                 TupE [ AppE f (VarE $ mkName "x"),

                        AppE g (VarE $ mkName "y")

```
                      ]
```

Die Funktion cross erwartet zur Konstruktion einer Lambda-Funktion zwei Ausdrücke f und g vom Typ Exp . Die Funktionen f und g werden auf das erste bzw. zweite Element eines übergebene Tupels angewandt, dessen Elemente mit x und y bezeichnet sind. Übergibt man nun die Ausdrücke VarE $ mkName "x" und VarE $ mkName "y" als Parameter an die Funktion cross, meldet der Compiler zunächst keinen Fehler. Wandelt man diesen Ausdruck aber in Haskell-Code um, so führt dies beim Compiler zu folgender Fehlermeldung:


Occurs check: cannot construct the infinite type: t = t -> t1
Probable cause: `x' is applied to too many arguments
In the expression: x x
In the expression: (x x, y y)

Die Fehlermeldung besagt, dass es nicht möglich ist, einen undendliche Typen t = t -> t1 zu konstruieren. Der Grund dafür wird ersichtlich, wenn man sich den erzeugten Ausdruck genauer anschaut: \ (x, y) -> (x x, y y). Es ist ersichtlich, dass hier die Funktionsnamen nur eingesetzt werden, ohne Kennzeichnung, dass diese zu einem anderen (äußeren) Scope gehören. Um dieser Art Scoping-Fehler vorzubeugen, existiert im Layer 1 eine Hilfsstruktur, auf die im nächsten Kapitel näher eingegangen wird - die Q-Monade

3.2 Die Q-Monade

Die Q-Monade ist konzeptionell nichts anderes als eine Erweiterung der IO-Monade um eine Environment. Dieses Environment speichert wichtige Informationen, von denen hier erstmal nur eine von Interesse sein soll - nämlich: eine Art "globaler" Namenspeicher. Dieser nimmt eine wichtige Rolle bei der Erfüllung des Hauptzwecks der Q-Monade ein, welcher darin besteht, die Erzeugung von Namen zu übernehmen, sodass es nicht zu Namenskonflikten kommen kann, wie bei der Verwendung der Funktion mkName. Die Template Haskell Bibliothek definiert für die Erzeugung sog. "frischer" Namen daher eine Funktion newName :: String -> Q Name, welche die Generierung einzigartiger Namen sicherstellt.

Wie aus der Signatur der Funktion newName ersichtlich wird, kann selbige nur innerhalb der Q-Monade verwendet werden. Für die zuvor vorgestellten Typkonstruktoren bedeutet dies, dass diese ebenfalls in Monadenform gebracht werden müssen. Das heißt: Anstelle von einfachen Datenwerten (Exp, Pat, etc) wird nun mit monadischen Berechnung gearbeitet, deren Ergebnisse die Datenwerte darstellen. Um einen Datentypen in die Q-Monade mittels return "einwickeln" zu können, muss dieser lediglich Instanz einer sogenannten Quasi-Klasse sein. Bezogen auf die objektorientierte Welt, bildet die Quasi-Klasse damit eine Art Interface. Für die weitere Betrachtung soll es an dieser Stelle genügen, zu wissen, dass die bereits erwähnten Datentypen (Exp, Pat, etc.) dieses Interface implementieren und in der Q-Monade verwendet werden können. Die monadische Version einer Exp lautet bspw. Q Exp, die eines Patterns Q Pat etc. In der Bibliothek existiert eine Reihe von Typsynonymen zur verkürzten Schreibweise. Anstelle von Q Exp kann man daher einfach ExpQ schreiben; dies gilt analog auch für die anderen Datentypen.

Das im vorherigen Kapitel gezeigte Beispiel, in dem es unter Verwendung von mkName zu Namenskonflikten bei der Funktion cross kommt, kann unter Verwendung von newName in der Q-Monade wie folgt umgeschrieben werden:

```
cross :: ExpQ -> ExpQ -> ExpQ
```
```
cross f g = do  
```
```
            x <- newName "x"
```
```
            y <- newName "y"
```
```
            ft <- f
```
```
            gt <- g
```

            return (LamE [ TupP [ VarP x,

                                  VarP y

```
                                ]
```
```
                         ]
```

                         ( TupE [ AppE ft (VarE x),

                                  AppE gt (VarE y)

```
                                ]
```
```
                         )
```
```
                   )
```

Die wesentliche Änderung gegenüber dem Beispiel ohne Monade befindet sich in den Zeilen drei und vier. Statt die Variablen x und y in der Funktion mittels mkName "..." zu generieren, werden diese über eine monadische Berechnung mit newName "..." erzeugt.

Der Funktion cross können nun wieder die Parameter VarE $ mkName "x" und VarE $ mkName "y" übergeben werden, wenn diese zuvor mit return in die monadische Form gebracht werden. Die Betrachtung der Typen des Top-Level-Splices \(x[a1Ac], y[a1Ad]) -> (x x[a1Ac], y y[a1Ad])zeigt nun, dass die Namen x und y in der Funktion cross umbenannt wurden in x[a1Ac] und y[a1Ad]. Auf diese Weise ist sichergestellt, dass von außen (über Parameter) injizierte Namen keine Namenskonflikt verursachen können. Angemerkt sei an dieser Stelle noch, dass es durch die Q-Monade egal ist, welcher String an newName übergeben wird, solange dieser nicht leer ist. In dem obigen Beispiel hätte für x und y daher auch beide Male newName "x" aufgerufen werden können.

3.2.1 Von den ADTs zum Objektprogramm

Wie bereits im vorherigen Kapitel erwähnt, können die ADTs durch return in die monadische Form gebracht werden. Aus der monadischen Form kann dann mithilfe des sog. Splice-Operators ($) wiederum der Objektcode erzeugt und genutzt werden. Damit der Compiler den Splice-Operator erkennt, muss die Compiler-Option -XTemplateHaskell angegeben werden. Die folgenden Aufrufe im ghci verdeutlichen den eben geschilderten Zusammenhang. Das kommando :t im ghci bestimmt den Typ eines Ausdrucks.


> let f = LamE [VarP $ mkName "x"] (VarE $ mkName "x")

> :t f
f :: Exp

> let g = $(return f)

> :t g
g :: t -> t

> g 42
42

Um aus einem Q-monadischen Ausdruck wieder die berechneten ADTs zu extrahieren, existiert in der Bibliothek die Funktion runQ, die wie folgt verwendet werden kann.


> runQ (return f)
LamE [VarP x] (VarE x)

Wie aus den obigen Beispielen ersichtlich wird, müssen die ADTs stets erst in die monadische Form gebracht werden, damit die Funktionen runQ und ($) auf diesen ausgeführt werden können. Um diesen Zwischenschritt zu vermeiden, wurde in der Template Haskell Bibliothek der zweite Layer der Syntaxkonstruktionen eingeführt, auf den im nächsten Kapitel näher eingegangen wird.

3.2.2 Syntax-Konstruktionsfunktionen

Bei den Syntax-Konstruktionsfunktionen handelt es sich um die monadischen Versionen der Typkonstruktoren. Der Name der Syntax-Konstruktionsfunktion zu einem Typkonstruktor ergibt sich - nach Namenskonventionen - , indem man den ersten Buchstaben des selbigen klein schreibt. Die Verwendung dieser Funktionen wird in dem folgenden Beispiel aufgezeigt. Ausgangspunkt stellt dabei die weiter oben definierte Funktion cross da, die hier nochmal aufgeführt ist:

```
cross :: ExpQ -> ExpQ -> ExpQ
```
```
cross f g = do  
```
```
            x <- newName "x"
```
```
            y <- newName "y"
```
```
            ft <- f
```
```
            gt <- g
```

            return (LamE [ TupP [ VarP x,

                                  VarP y

```
                                ]
```
```
                         ]
```

                         ( TupE [ AppE ft (VarE x),

                                  AppE gt (VarE y)

```
                                ]
```
```
                         )
```
```
                   )
```

In dieser ersten monadischen Definition der Funktion wurden die übergebenen Funktionen f und g in den Zeilen fünf und sechs selbst ausgewickelt und gebunden, um die eingwickelten Daten (Expr) zu erhalten, da der Konstruktor von App diese benötigt. Zudem wurde der so gebildete Ausdruck durch die return-Anweisung am Ende wieder eingewickelt. Um diesen Wechsel zwischen Ein- und Auspacken der Q-Monade zu verhindern und - nicht zuletzt - auch eine durchgehend monadische und kürzere Schreibweise zu ermöglichen, werden nun durchgängig die Syntax-Konstruktionsfunktionen verwendet, wie im folgenden Code ersichtlich:

```
cross :: ExpQ -> ExpQ -> ExpQ
```
```
cross f g = do  
```
```
            x <- newName "x"
```
```
            y <- newName "y"           
```
```
            (lamE [ tupP [ varP x, 
```
```
                           varP y
```
```
                         ]
```
```
                  ]
```

                  ( tupE [ appE f (varE x),

                           appE g (varE y)

```
                         ]
```
```
                  )
```
```
            )
```

3.2.3 Reifikation

Im vorherigen Kapitel wurde bereits auf das Environment der Q-Monade eingegangen. An dieser Stelle wird nun eine weitere Informationsquelle erläutert, die der Q-Monade im Environment zugreifbar ist - die Symboltabelle des Compilers. Diese Tabelle wird für die Reifikation benötigt. Unter Reifikation wird die Möglichkeit für ein Programm verstanden, den Status der internen Symbol-Tabellen des Compilers abzufragen. ¹⁷ Im Folgenden wird anhand eines exemplarischen Datentyps der Prozess der Reifikation veranschaulicht. Die Struktur des Datentyps wird dabei zunächst ausgelesen und anschließend verarbeitet.

3.2.3.1 Auslesen interner Datenstrukturen

Mit der Funktion reify :: Name -> Q Info ist es möglich, Informationen vom Typ Info zu beliebigen Namen zu erfagen, um diese zu analysieren und ggf. weiter zu verarbeiten. Exemplarisch wird dies im Folgenden für die unten aufgeführte Definition eines Typen Foo aufgezeigt:

```
data Foo a = MkFoo1 a
```
```
           | MkFoo2 a
```
```
           deriving (Show)
```

Versucht man eine Reifikation der Typdefinition von Foo innerhalb der IO Monade mit runQ $ reify $ mkName "Foo" durchzuführen (z.B. unter Verwendung des ghci), so erhält man jedoch folgende Fehlermeldung:

Template Haskell error: Can't do `reify' in the IO monad
*** Exception: user error (Template Haskell failure)

Der Grund dafür ist, dass das Environment der Q-Monade - und somit auch die Symbol-Tabelle des Compilers - zur Laufzeit nicht zur Verfügung stehen. Allerdings kann man mit folgendem Trick (auch im ghci unter Angabe des Flags -XTemplateHaskell) die gewünscht Funktionalität erreichen:

 $(stringE . show =<< (reify $ mkName "Foo") )

Der Operator =<< ist nichts anderes als der normale Bind-Operator der Monade mit einem flip versehen. Der durch (reify $ mkName "Foo") erzeugte Ausdruck vom Typ Q Info wird mittels der Funktionskomposition stringE . show zunächst in einen String umgewandelt und danach sofort wieder in den monadischen Ausdruck ExpQ überführt. Um das Ergebnis zur Compilezeit in einen String umzuwandeln, wird auf den gesamten Ausdruck der Splice-Operator angewandt. Dieser kann nun zur Laufzeit angezeigt werden.

Bezogen auf das obige Beispiel, erhält man folgende Informationen zum Datentyp Foo bei der Eingabe im ghci (hier umformatiert).

> $(stringE . show =<< (reify $ mkName "Foo") )
"TyConI ( DataD [] 
          MyModule.Foo 
          [a_1627422384] 
          [ NormalC MyModule.MkFoo1 
              [( NotStrict,
                 VarT a_1627422384)
              ],
            NormalC MyModule.MkFoo2
              [( NotStrict,
                 VarT a_1627422384)
              ],
          ] 
          []
        )"

Der Konstruktor TyConI gibt an, dass es sich bei Foo um eine Typkonstruktion handelt. Der Konstruktor weist eine Vielzahl an Parametern auf. So erfährt man vom zweiten Parameter den qualifizierten Namen MyModule.Foo des Typen Foo und somit auch den Namen des zugehörigen Moduls. Der dritte Parameter enthält eine Liste der verwendeten Typparameter - in diesem Fall existiert nur der Typparameter a_1627422384. Es folgt eine Liste der definierten Konstruktoren für Foo. Es ist ersichtlich, dass zwei Konstruktoren MkFoo1 und MkFoo2 vorhanden sind. Der Konstruktor NormalC gibt dabei an, dass es sich um "normale" Konstruktoren handelt, d.h. ohne zusätzliche Angaben wie bspw. {..}-Schreibweise der Attribute für den vereinfachten Zugriff. Zu jedem Konstruktor wird eine Liste von Informationen zu den Typparametern angegeben. Über diese erfährt man, dass die Typparameter hier nicht strikt sind und dass MkFoo1 und MkFoo2 den gleichen Typparameter verwenden.

3.2.3.2 Verarbeitung interner Datenstrukturen

Mithilfe der Reification konnten Informationen des Datentyps Foo ermittelt werden. Da es sich bei diesen Informationen auch nur um einfache Abstrakte Datentypen handelt, können auch hier wieder die gewohnten Analyse- und Destructuring-Methoden von Haskell angewandt werden. Im folgenden Beispiel werden nur anhand des Namens des Datentyps Foo, sämtliche "normale" Konstruktoren ausgelesen, um diese mit der Zahl 42 zu initialisieren.

-- Extrahiert Konstruktoren eines Datentyps

```
getConstructors :: Name -> Q [Con]
```
```
getConstructors name = do
```

                       (TyConI d) <- reify name

                       (DataD _ typeName _ constructors _) <- return d

                       return constructors

```
 
```

-- Wickelt die Zahl 42 in alle Konstruktoren des Datentyps

```
init42  :: Name -> ExpQ
```
```
init42 name= do
```

              constructors <- getConstructors name

              newInstances <- return $

                              map (\(NormalC cName _) -> appE (conE cName) (litE $ integerL 42))

                                  constructors

```
              listE newInstances  
```

In Zeile elf wird das Auslesen der Konstruktoren zunächst an eine Funktion getConstructors übergeben. Diese führt in Zeile vier die Reifikation durch. Das Pattern-Matching in Zeile fünf liest schließlich die Liste der Konstruktoren aus, die durch den Konstruktor NormalC repräsentiert werden. Aus der vorangegangenen Analyse ist bekannt, dass der Konstruktor NormalC als zweiten Parameter den Konstruktornamen enthält. Durch ein einfaches Mapping über die Liste der Konstruktoren in Zeile dreizehn ist es daher möglich, die Konstruktornamen cName zu matchen und als Parameter für den Konstruktor-Konstruktor conE zu verwenden. Durch appE wird der conE hier mit der (litE $ integerL 42) initialisiert.

Um die initialisierten Konstruktoren anzeigen zu lassen, kann man nun folgenden Code verwenden.

```
showInits42 = do
```

              cs <- $(init42 $ mkName "Foo")

```
              return cs 
```

Das Ergebnis des Aufrufs von showInits42 liefert dann:


> showInits 42
[MkFoo1 42,MkFoo2 42]

3.2.3.3 Instance deriving

Das im vorherigen Abschnitt gezeigte Beispiel des Auslesens der Konstruktoren zwecks Initialisierung kann noch allgemeiner gefasst werden. Angenommen, man hat eine Klasse Class42 mit folgender Struktur:

```
class Class42 a where
```
```
   init_42 :: a -> Int
```

Nun soll ein Datentypen mit einem Typparameter automatisch zu einer Instanz der Klasse Class42 gemacht werden können, so wie dies aus Haskell durch die Angabe von deriving für andere Typklassen (z.B. Show, Ord, Num, ...) möglicht ist.

Die eigentliche Idee besteht darin, eine instance-Deklaration anhand eines Namens zu erzeugen. Diese Aufgabe soll die Funktion gen_Class42 übernehmen. Bezogen auf unsere obige Klasse, soll dann die Angabe $(gen_Class42 $ mkName "Foo") folgenden Code zu Compilezeit im Quellcode erzeugen:

```
instance Class42 (Foo a) where
```
```
   init_42 (MkFoo1 x) = 42
```
```
   init_42 (MkFoo2 x) = 42
```

Eine Funktion, die genau dies leistet, ist im Folgenden abgebildet. Zum besseren Verständnis und Vermeidung unnötiger Komplexität, funktioniert diese Funktion nur für Datentypen T der Art * -> * und auch nur dann, wenn alle Konstruktoren der Art a -> T a sind. Auf eine Fehlerbehandlung wurde somit verzichtet, um den Code übersichtlich zu belassen.

```
generic_Class42 :: Name -> Q [Dec]
```
```
generic_Class42 name = do
```

                       constructors <- getConstructors name

                       top <-  return $

                               InstanceD []

                               ( AppT (ConT $ mkName "Class42")

                                      (AppT (ConT name) (VarT $ mkName "a") )

```
                               ) 
```
```
                               [
```
```
                                  FunD 
```

                                  (mkName "init_42") $

                                  map ( \(NormalC cName _) -> Clause

                                                              [ConP cName [VarP (mkName "x")]]

                                                              (NormalB $ LitE $ IntegerL 42)

                                                              [] -- no further declarations

```
                                      )
```

                                    constructors

```
                               ]
```
```
                       return [top] 
```
```
 
```

In Zeile drei werden zunächst wieder die Konstruktoren des Datentyps ausgelesen. Ab Zeile fünf wird der Konstuktor InstanceD definiert, um die Instanzdeklaration zu erzeugen. Die Zeile sechs und sieben stehen für instance Class42 (T a), wobei T ein beliebiger Datentyp ist, der die oben genannten Restriktionen erfüllt. Die Funktionsklauseln für die in der Klasse Class42 definierte Funktion init_42 werden ab Zeile zehn durch den Konstruktor FunD angegeben. Das Mapping in Zeile zwölf hat die Aufgabe, die Namen aus den gefundenen Konstruktoren zu extrahieren und aus diesen jeweils einen Kostruktor-Pattern für eine Klausel der Funktion init_42 zu erzeugen, welcher dann auf die Zahl 42 abbildet. Konkret werden hier, bezogen auf die Klasse Foo, die Funktionsklauseln init_42 (MkFoo1 x) = 42 und init_42 (MkFoo2 x) = 42 erzeugt.

3.3 Quasi-Quotes in Template Haskell

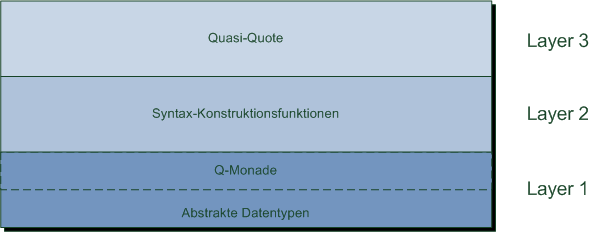
Die letzte bzw. oberste Schicht in der Architektur der Template Haskell Bibliothek bilden die Quasi-Quotes, welche die eigentlichen Templates in Template Haskell bilden, denn: Mithilfe der Quasi-Quotes ist es möglich, eine eigene domain-spezifische Syntax zum Erzeugen von Programm-Fragmenten zu verwenden. Der Quasi-Quoter hat also die Aufgabe, eine abstrakte Syntax in Form eines Strings in einen Syntaxbaum zu parsen. ¹⁸ Damit handelt es sich bei dieser Schicht um eine reine Komfort-Schnittstelle für den Nutzer. Die Realisierung dieses Komforts bringt allerdings einige Probleme mit sich, auf die im Folgenden eingegangen wird. Dabei wird zunächst der allgemeine Nutzen von Quasi-Quotes erläutert.

Quasi-Quotes allgemein

Das Prinzip der Quasi-Quotes wird anhand eines kleinen Beispiels deutlich. Angenommen, man will eine abstrake Sprache zum Durchführen der vier Grundrechenarten implementieren. Der erste Schritt besteht darin, eine Datentyp-Repräsentation für mathematische Ausdrücke zu entwickeln. Diese könnte bspw. wie folgt aussehen:

```
data Expr  = IntExpr Integer
```

           | BinopExpr (Integer -> Integer -> Integer) Expr Expr

```
           deriving(Show)
```

In einem zweiten Schritt muss nun ein Parser implementiert werden, der in der Lage ist, Ausdrücke wie z.B. 1 + 2 in den Datentyp Expr zu transformieren. An dieser Stelle wird nicht weiter auf die genaue Implementierung eines solchen Parsers eingegangen, da es für das weitere Verständnis dieser Ausarbeitung nicht notwendig ist. Es reicht, an dieser Stelle zu wissen, dass ein eigener Parser in der Lage sein muss, Patterns und Ausdrücke aus der eigenen abstrakten Syntax zu unterscheiden.

Angenommen, die Funktion quoter erzeugt also einen solchen Parser für die mathematischen Ausdrücke, dann kann dieser zur Auswertung des Strings 1 + 3 + 5 wie folgt aufgerufen werden¹⁹:


> [expr|1 + 3 + 5|]
  BinopExpr AddOp (BinopExpr AddOp (IntExpr 1) (IntExpr 3)) (IntExpr 5)

Wie aus der Eingabe ersichtlich wird, hat ein Quasi-Quote die Form: [p|exp|], wobei p ein Parser und exp der zu parsende String ist. Diese Notation wird auch Bracket-Schreibweise genannt. Damit der Compiler Quasi-Quotes interpretieren kann, muss beim Kompilieren zusätzlich das Flag -XQuasiQuotes angegeben werden. In der zweiten Zeile, der Ausgabe, ist der erzeugte Syntaxbaum angegeben.

Quasi-Quotes in Template Haskell

Zur Erzeugung von Haskell Templates stellt die Template Haskell Bibliothek eine Reihe von Quasi Quotern bereit, welche in diesem Zusammenhang als Kontexte bezeichnet werden. Diese sind im Paket Language.Haskell.TH.Quote.QuasiQuoter definiert. Für jeden Kontext wird ein eigener Parser verwendet, der durch einen der Buchstaben 'e','p','d' im Quasi-Quote für den Platzhalter p eingesetzt wird. Bei fehlender Angabe eines Parsers wird implizit der Parser für Ausdrücke 'e' angenommen. In Abhängigkeit des Parsers ändert sich die zulässige Syntax des Strings. An dieser Stelle sei angemerkt, dass die Parser für Patterns und Typdefinitionen in der aktuell vorliegenden Template Haskell Version (2.5.0.0) noch nicht funktionieren.

Überträgt man die monadische Version der Funktion cross in Quasi-Quotes, so ergibt sich der folgende Code:

```
cross :: ExpQ -> ExpQ -> ExpQ
```

cross f g = [| \ (x,y) -> ($f x, $g y) |]

Die Bracket-Schreibweise erlaubt es dem Nutzer also gewöhnlichen Haskell-Code zu verfassen, der dann durch den Compiler in einen ExpQ (also einen monadischen Ausdruck) übersetzt wird. Somit kann der Splice-Operator $ auch auf Quasi-Quotes angewendet werden. Da cross aber vom Typ ExpQ -> ExpQ -> ExpQ ist, Splices aber nur auf Ausdrücke vom Typ ExpQ angewendet werden können, müssen die beiden Parameter f und g zuvor gebunden werden. Hierbei fällt auf dass diese innerhalb des Templates wiederum in Form eines Splices auftauchen.

Ein Splice innerhalb eines Quasi-Quotes bedeutet: Wenn beim Kompilieren eines Quasi-Quotes ein Splice gefunden wird, dann wird dieser zu Compilezeit ausgeführt und der resultierende Ausdruck an dessen Stelle eingefügt, so, als hätte der Entwickler diesen selbst eingegeben.²⁰ Die Ausführung von Programmcode zur Compilezeit führt damit zu einem mehrstufigen Kompiliervorgang, auf den im nächsten Kapitel näher eingegangen wird.

Aus dem folgenden Beispiel wird ersichtlich, dass man der Funktion cross als Parameter ebenfalls Quasi-Quote Ausdrücke übergeben kann. In diesem Fall werden die Funktionen x und y in Quasi-Quotes als Parameter verwendet.


> let x = (+)1
> let y = (*)1
> let foo = cross [|x|] [|y|]
:t foo :: ExpQ

> let bar = $foo
> :t bar
bar :: (Integer, Integer) -> (Integer, Integer)

> bar (1,2)
(2,2)

Da es sich bei foo um einen ExpQ handelt, kann man sich mithilfe der Funktion runQ den erzeugten Syntaxbaum zu foo anzeigen lassen.


> runQ foo
LamE [TupP [VarP x_2,VarP y_3]] ( TupE [ AppE (VarE x_1627429000) 
                                              (VarE x_2),
                                         AppE (VarE y_1627429038) 
                                              (VarE y_3)
                                       ]
                                )

Wie man erkennen kann, wurden die Template Variablen x und y auch hier korrekt umbenannt, so dass es zu keinem Namenskonflikt mit den übergebenen gleichnamigen Funktionen aus einem anderen Scope kommt.

Grenzen von Quasi-Quotes

Das obige Beispiel zeigt, dass Quasi-Quotes eine gute Möglichkeit sind, um komplexe Ausdrücke automatisch vom Compiler generieren zu lassen. Allerdings lassen sich mit den Quasi-Quotes nicht alle Sachverhalte darstellen, sodass man oft weiterhin auf die Syntax-Konstruktionsfunktionen angewiesen ist. So ist bspw. jede Form der Algorithmenkonstruktion nur mit Quasi-Quotes nicht umsetzbar. Man denke z.B. an die Konstruktion einer Funktion, die bei einem beliebig langen Tupel das n-te Element ausgeben kann. Unter Kenntnis der Größe n des Tupels muss somit ein entpsrechendes Pattern eingegeben werden. In Quasi-Quotes müsste man somit einen Ausdruck der Art [|\n (a1,a2,...,an) -> an |] konstruieren; genau diese Konstruktion an der Stelle ... ist aber nicht möglich. Die Lösung dieses Problems wird in dem Kapitel zu den Anwendungsbeispielen erörtert.

3.3.1 Typüberprüfung in Templates

Bei Haskell handelt es sich um eine streng getypte Sprache. Daraus folgt, dass alle Typüberprüfungen zur Compile-Zeit vorgenommen werden, sodass zur Laufzeit keine Typverletzungen mehr auftreten können. Für gewöhnlich leiten sich daraus folgende sequentiell ablaufende Arbeitsschritte ab:

Typcheck /-überprüfung
Kompilierung
Ausführung

Diese strikte Abfolge der Arbeitsschritte kann bei Verwendung von Templates jedoch nicht eingehalten werden. Vielmehr werden Typcheck und Ausführung zur Compilezeit miteinander vermischt, sodass der Typcheck sich über mehrer Phasen vollzieht. Die Phasen bzw. Stufen des Kompilierungsvorgangs werden im Folgenden näher betrachtet.

3.3.1.1 Mehrstufige Kompilierung

Beim Kompilieren von Haskell Templates, lassen sich insgesamt drei Zustände unterscheiden, in denen sich der Compiler befinden kann. Diese Zustände, ersichtlich in der unten stehenden Abbildung 2, sind durch Zustandsübergänge miteinander verbunden. ²¹

Abbildung 2 Zustände beim Typcheck für Template Haskell

Im Zustand C befindet sich der Compiler für gewöhnlich, wenn statischer Haskell Code kompiliert wird. Von diesem Zustand sind Übergänge in die Zustände B (durch einen Quasi Quote) und S (durch einen Splice) möglich - von diesen aus existieren jedoch keine Übergänge zurück zu C. Befindet sich der Compiler im Zustand B, bedeutet dies, dass Ausdrücke innerhalb eines Quasi Quotes verarbeitet werden. Wird innerhalb eines solchen Quasi-Quotes ein Splice entdeckt, so führt dies dazu, dass dieser vom Compiler im Zustand S berechnet und somit komplett ausgewertet wird. Das Ergebnis wird dann an die Aufrufstelle innerhalb des Quasi-Quotes eingesetzt, so, als hätte der Programmierer den Ausdruck selbst geschrieben. Sofern innerhalb eines Splices wiederum Quasi-Quotes gefunden werden, wechselt der Compiler wieder zurück in den Zustand B.

Die in Abbildung 2 dargestellten Übergänge sind die einzig möglichen Übergänge. Nicht aufgeführte Übergänge sind demnach unzulässig und führen zu Kompilierungsfehlern.

3.3.1.2 Regeln beim Typcheck

Damit der Compiler die im vorherigen Kapitel erläuterten Zustände und Zustandsübergänge umsetzen und prüfen kann, ist es notwendig, dass diese durch formale Regeln beschrieben werden. Im Folgenden wird eine solche Regel exemplarisch vorgestellt, wobei zuvor auf die verwendete Nomenklautur einzugehen ist:

Abbildung 3 Nomenklatur für Regeln beim Typcheck

Das große Gamma ganz links in Abbildung 3 steht für eine Art Verzeichnis, in dem alle Variablen auf ihren Typ und das aktuelle Binding abgebildet werden. Das s steht für einen der Zustände aus dem Zustandsübergangsdiagramm, das e für einen beliebigen Ausdruck und das kleine Tau für einen Typen. Zusätzlich wird noch eine Zählervariable n für die Schachtelungstiefe verwendet, um Top-Level-Splices und Splices innerhalb von Quasi-Quotes voneinander zu unterscheiden. n ist zu Beginn 0 und wird bei jedem Betreten von Brackets inkrementiert, bei einem Splice dekrementiert. Die Regeln werden - wie in der unteren Abbildung ersichtlich -in Form eines Bruchs definiert, wobei der Zähler die Voraussetzung und der Nenner den daraus zu ziehenden Schluss enthält.

Abbildung 4 Regel für Brackets

Die in Abbildung 4 dargestellte Formel besagt z.B.: Wenn ein Ausdruck e vom Typ Tau im Zustand B in einer Tiefe von n+1 gefunden wird, dann muss sich e innerhalb eines Quasi-Quotes in einer um eins geringeren Tiefe befinden und in einem der beiden Zustände C oder S sein, wobei der Typ allgemein Q Exp gewesen sein muss. Durch diese Regel wird ausgedrückt, dass Brackets nicht geschachtelt werden können. In dem folgenden Beispiel wird gezeigt, zu welcher Fehlermeldung der Versuch, dies zu tun, führt.


> [| 1 + [|2|] |]

Illegal bracket at level Brack 2
In the second argument of `(+)', namely `[| 2 |]'
In the expression: 1 + [| 2 |]
In the expression: [| 1 + [| 2 |] |]

Beim Finden der 2 vom Typ Int befindet sich der Compiler nach zweimaligem Inkrementieren von n auf Level 2 (durch die beiden Brackets) im Zustand B. Wenn dies gilt, dann folgt daraus, dass die 2 im vorherigen Level in Brackets aufgetaucht sein muss. Dies stimmt soweit. Allerdings gilt die Zustandsbedingung nicht, die besagt, dass der Compiler sich in einem der beiden Zustände C oder S befinden muss - tatsächlich befindet dieser sich nämlich wiederum im Zustand B. Somit weiß der Compiler, dass das zweite Argument von (+) als Bracket nicht erlaubt ist, was in der Fehlermeldung zum Ausdruck kommt.

3.3.1.3 Compilezeit-orientiertes Staging

Templates können nur zur Compile-Zeit erzeugt werden, da Template Haskell rein Compile-Zeit orientiert ist. Daraus folgt, dass alle Variablen, welche zur Erzeugung eines Templates benötigt werden, zur Compile-Zeit bekannt sein müssen. Wird versucht, einem Template eine Variablen zuzuweisen, die sich erst zur Laufzeit berechnen lässt, so führt dies zu einem sogenannten Staging Error. In dem folgenden Beispiel ist dies exemplarisch gezeigt.²²

```
bar :: ... -> ExpQ
```
```
bar = ...
```
```
 
```
```
foo x = $(bar x)
```

Die Funktion foo erwartet einen Parameter x, welcher an eine Funktion bar übergeben wird. Das Ergebnis der Berechnung von bar x ist ein ExpQ. Nach dem obigen Ausdruck, könnte die Template Funktion bar somit erst zur Laufzeit berechnet werden, wenn x bekannt ist - und das ist nicht erlaubt. Befindet sich der Ausdruck $(bar x) hingegen in Quasi-Klammern, also [| $(bar x) |], so führt dies zu keinem Staging-Error, da die Funktion foo nun selbst eine Template Funktion vom Typ Exp ist.

3.3.2 Statisches Scoping von Quasi-Quotes

Da es sich bei der Syntax innerhalb der Quasi-Quotes um einfachen Haskell Code handelt, könnte man zu der Annahme kommen, dass für diesen ohne großen Aufwand ein statisches (lexikalisches) Scoping durchgeführt werden kann. Ein Problem bei der Umsetzung des Scopings, ist allerdings die durch die mehrstufige Kompilierung bedingte Erzeugung neuen Codes zur Compilezeit. Es muss also die Frage beantwortet werden, wie Namenskonflikte, die durch die Expansion von Templates in anderen Templates entstehen können, zu verhindern sind - die Antwort lautet: Pre-Expansions-Binding. Konkret bedeutet dies, dass alle Namen eines Templates lexikalisch an ihre Umgebung gebunden werden und zwar bevor das Template expandiert wird.²³

Durch Pre-Expansions-Binding werden sogenannte "unhygienische Macros" vermieden, bei denen die Expansion innerhalb eines Programmes dazu führen kann, dass Bindings auf Objektebene überschrieben werden.²⁴ Deutlich wird dies an dem folgenden Beispiel:

```
foo = \x -> $(f [| x |])
```
```
 
```
```
f :: ExpQ -> ExpQ
```
```
f e = [| \x -> $e |]
```

Die Expansion des Templates f im Ausdruck von foo würde - bei einem unhygienischen Macro - dazu führen, dass x nicht mehr an das Pattern x der Lambda-Funktion von foo gebunden wird. Stattdessen expandiert f selbst zu einer Lambda-Funktion, die das Binding für x überschreibt. Man erhielte somit für foo den Ausdruck \x1 -> \x -> x.

Da Haskell - wie bereits erwähnt - jedoch alle Variablen vor der Expansion der Templates bindet, wird das im Template f [| x |] verwendete x an die äußere Lambda-Funktion gebunden, womit foo gleichwertig ist zu dem Ausdruck \x -> \x1 -> x

Die Tatsache, dass die Quasi-Quotes auf der Q-Monade basieren, führt dazu, dass Template-Variablen umbenannt werden, damit diese nicht unbeabsichtigter Weise falsch gebunden werden können. Der Quasi-Quote [| \x -> \x -> x |] führt bei einem Splice daher stets zu dem Ausdruck \x1 -> \x -> x. Wie kann man diese Ausdruck aber nun unter Verwendung des Templates f generieren? Die Antwort auf diese Frage ist die Antwort auf eine andere Frage, nämlich: Wie kann das Pre-Expansions-Binding umgangen bzw. umgewandelt werden in ein Post-Expansions-Binding, ein Binding also, dass erst nach der Expansion des Templates vorgenommen wird. Die Antwort lautet: Dynamisches Binding. Da das dynamische Binding im Grunde nichts anderes ist als das bewusste Umgehen der sog. Cross-Stage-Persistenz, wird diese im folgenden Abschnitt zunächst erläutert.

3.3.3 Cross-Stage Persistenz

Der Begriff Cross-Stage Persistenz meint zunächst nicht anderes, als die Fähigkeit, Werte von zur Compile-Zeit existenten Variablen in den erzeugten Code einzubinden. Haskell unterscheidet dabei zwischen Variablen mit Top-Level-Binding und lokal gebundenen Variablen. Auf die jeweiligen Konzepte und Implementierungen wird im Folgenden eingegangen.²⁵

3.3.3.1 Cross-Stage Persistenz für Top-Level-Bindings

Die Cross-Stage Persistenz dient dem Zweck, sicherzustellen, dass die innerhalb eines Templates bzw. Quasi-Quotes stehenden Namen beim Splice immer an Werte des ursprünglichen Scopes gebunden werden - unabhängig davon, wo der Splice stattfindet. Deutlich wird dies an dem folgenden Beispiel²⁶:

```
module T( genSwap ) where
```
```
  swap (a,b) = (b,a)
```
```
  genSwap x = [| swap x |]
```
```
 
```
```
module Foo where
```
```
  import T( genSwap )
```
```
  swap = True
```
```
  foo = $(genSwap (4,5))
```

Im Modul T wird eine Template-Funktion genSwap zum Vertauschen von Werten eines Tupels definiert und exportiert. Innerhalb der Quasi-Quotes wird der Name swap die an gleichname Funktion im Namensraum T gebunden (Top-Level Binding) - diese wird allerdings nicht exportiert. In einem anderen Modul Foo wird die Funktion genSwap importiert, und die Funktion foo führt auf dieser einen Splice aus. Der Splice führt schließlich zu einem Aufruf der Funktion swap, welche aber nicht exportiert wurde von T. Innerhalb des aktuellen Scopes - nämlich der Namensraum des Moduls Foo - findet sich ebenfalls eine Funktion swap. Diese kann (wegen Typindifferenz) aber nicht vom Template verwendet werden.

Die Lösung dieses Problems stellt das Konzept der urspünglichen Namen dar, welches den Compiler beim Splice-Vorgang dazu veranlasst, die Namen innerhalb eines Templates mit ihrem usprünglichen Namen anzugeben. Konkret bedeutet dies, dass jeder Name einen Präfix der Form M: enthält, wobei M für den Modulnamen steht. Der Splice im obigen Beispiel wird daher als T:swap (4,5) in Foo eingefügt.²⁷

An dieser Stelle sei angemerkt, dass die Angabe von ursprünglichen Namen nur durch eine Spracherweiterung von Haskell möglich ist, auf welche Template Haskell zurückgreift. Die Angabe des ursprünglichen Namens ist bei "normalen" Haskell Funktionen nicht möglich. Die Angabe des qualifizierten Namens, also T.swap, würde nicht funktionieren, da dies ebenfalls voraussetzt, dass swap von T exportiert wird.²⁸

3.3.3.2 Cross-Stage Persistenz für lokale Bindings

Zur Erläuterung der Cross-Stage Persistenz für lokale Bindings, wird noch einmal die Funktion genSwap aus dem vorherigen Kapitel näher betrachtet.

```
module T( genSwap ) where
```
```
  swap (a,b) = (b,a)
```

  genSwap x = [| swap x |]  -- x wird lokal gebunden, swap global zu T

Innerhalb der Quasi-Quotes wird auf einen Namen x zugegriffen. Dieses x weist, anders als das swap, aber kein Top-Level-Binding in dem zugehörigen Modul auf, sondern ist lokal an das x-Pattern der Lamda-Funktion gebunden. Dies führt dazu, dass zur Compile-Zeit über x nur eine Information bekannt ist - nämlich der Typ. Die Angabe eines ursprünglichen Namens, wie bei den Top-Level-Bindings, ist daher nicht möglich. Trotzdem muss gewährleistet werden, dass der an x beliebig gebundene Ausdruck von den Quasi-Quotes "akzeptiert" werden kann. Erreicht wird dies durch die implizite Annahme des Class-Constraints Lift t für x, wobei t die Typvariable für x ist. Mithilfe dieser Klasse können beliebige Werte in einen Exp transformiert bzw. angehoben werden - vorausgesetzt, es existiert für diese eine Instanz der Klasse Lift. Die Signatur der Klassendefinition und zwei Beispiel-Implementierungen aus der Template Haskell Bibliothek für Integer und Tupel sind im folgenden Code ersichtlich.²⁹

```
class Lift t where
```
```
  lift :: t -> ExpQ
```
```
 
```
```
instance Lift Int
```
```
  lift n = litE (IntegerL n)
```
```
 
```

instance (Lift a, Lift b) => Lift (a,b) where

```
  lift(a,b) = tupE [lift a, lift b]
```

Der unten stehende Code zeigt, wie beim Überführen des Quasi-Quotes [| swap x |] in die Q-Monadenform durch den Compiler, der lokal gebundene Name x in Zeile 3 durch das lift angehoben wird, wohingegen swap seinen ursprünglichen Namen T:swap erhält. Schlägt das Liften innerhalb der Monade fehl, wird für die gesamte Berechnung ein Fehler zurückgegeben.

```
genSwap :: (Int,Int) -> ExpQ
```
```
genSwap x = do 
```
```
            t <- lift x
```

            return (App (Var "T:swap") t)

3.3.3.3 Dynamisches Binding

Wie bereits erwähnt, besteht die Grundidee des dynamischen Bindings im Aushebeln der Cross-Stage-Persistenz. Dazu muss nur verhindert werden, dass die global gebundenen Namen innerhalb eines Templates beim Aufruf aus einem anderen Modul durch ihren ursprünglichen Namen ersetzt werden. Dem Compiler bleibt beim Splice in einem anderen Modul dann nichts anderes übrig, als dessen Scope nach einem passenden Binding zu durchsuchen. "Dynamisch" meint in diesem Zusammenhang somit, dass das Ergebnis eines Splices abhängig ist vom Ort der Template-Applikation bzw. dessen Scope. Für das dynamische Binding stellt Template Haskell die Funktion dyn :: String -> ExpQ bereit.

```
genSwapDyn x = [| $(dyn "swap") x |]
```

Das obige Beispiel zeigt die dynamische Version der Funktion swap an. Der Name wird der Funktion dyn übergeben, welche diesen dann im Scope des Splice-Ortes bindet.