• Monomorphe Typüberprüfung
• Polymorphe Typüberprüfung
• Typüberprüfung bei Klassen
  

In diesem Kapitel wird erklärt, wie Haskell es schafft, einen Ausdruck auf Typkorrektheit zu prüfen und wie ohne Angabe der Signatur der Typ eines Ausdrucks mittels Typinferenz ermittelt werden kann.

Das Überprüfen von monomorphen Typen ist sehr einfach. Als Beispiel sei dieser Ausdruck gegeben:

ord 'c' + 3

Die Signaturen der ord-Funktion und des + -Operators lauten:

ord :: Char -> Int
(+) :: Int -> Int -> Int

Bei der Typüberprüfung des obigen Ausdrucks wird zuerst bei der ord -Funktion geprüft, ob, wie in der Signatur gefordert, auch ein Wert vom Typ Char als Parameter steht. Dem ist so. Als nächstes wird bei dem + -Operator überprüft, ob als Parameter Werte vom Typ Int stehen. Die Char -Funktion liefert einen Int zurück. Der erste Parameter stimmt also. Der zweite Parameter ist ein Wert vom Typ Int und stimmt auch. Somit ist dieser Ausdruck typkorrekt. Der folgende Ausdruck ist nicht typkorrekt, da es sich bei dem zweiten Parameter für den + -Operator um einen Wert vom Typ Bool handelt, passt also nicht zu der Signatur des + -Operators

ord 'c' + False

f :: t1 -> t2 -> ... -> tk -> t

f p1 p2 ... pk
  | g1     = e1
  | g2     = e2
  ...
  | gn     = en

• Jeder "Guard" gi muss vom Typ Bool sein
• Jeder Ausdruck ei muss vom Typ t sein
• Jedes pj muss zum Typ tj passen

Bisher wurde zu den einzelnen Funktionen stets deren Signatur mit dazu geschrieben. Dies ist in Haskell aber nicht nötig, da Haskell aufgrund des Hindley-Milner Typsystems in der Lage ist, die Signatur ungetypter Ausdrücke selbst zu ermitteln. Dieser Prozess wird mit dem Begriff Typinferenz beschrieben. Bei polymorphen Typen ist dies aber ein wenig komplizerter, da es mehrere verschiedene Möglichkeiten gibt, wie sich eine Signatur zusammensetzt. Um dieses Problem zu lösen, ist ein Algorithmus nötig, welcher eine bestimmte gewünschte Signatur ausfindig macht. Sinnvoll ist dabei, die Signatur zu finden, welche die allgemeinste Form besitzt. Im folgenden soll an einem einfachen Beispiel erklärt werden, wie Haskell eine Typsignatur bestimmt.

Gegeben ist folgende Funktion:

f (x,y) = (x,['a' .. y])

Die Signatur läßt sich leicht ablesen. Der erste Parameter der Funtion ist ein Tupel mit 2 Variablen. Die erste Variable x des Tupels kann von irgendeinem Typ sein. Es muß also als ein polymorpher Datentyp gesetzt werden. Bei der 2. Variable im Tupel muß es sich, aufgrund von ['a' .. y], um einen Char -Typ handeln. Das Ergebnis der Funktion ist wiederum ein Tupel, bei dem auch hier die erste Variable ein polymorpher datentyp sein muß und die 2. Variable eine Liste von Char. Die Signatur sieht also folgendermaßen aus:

f :: (a,Char) -> (a,[Char])

Nun eine zweite Funktion:

g (m,zs) = m + length zs       -- length sei gegeben mit der Signatur: length  :: [b] -> Int

Auch hier ist nur eine Parameter vorhanden. Es ist ein Tupel aus 2 Variablen. Aufgrund des + -Operators muß die Variable m ein numerischer Wert sein. Da der Wert von m aber zusammen mit dem Ergebnis der length -Funktion addiert wird und die length -Funktion als Ergebnis einen Wert vom Typ Int zurückliefert, hat m auch Int zu sein. Die zweite Variable zs des Tupels muß aufgrund der Verwendung in der length -Funktion eine Liste mit einem polymorphen Datentyp sein. Der Ergebnistyp von der Funktion wird durch den + -Operator bestimmt, muß also auch Int sein. Die Signatur sieht so aus:

g :: (Int, [b]) -> Int

Zum Schluß noch eine dritte Funktion, die sich aus den Funktionen f und g zusammensetzt:

h = g . f

Die Komposition g . f bedeutet, dass das Ergebnis der Funktion f als Parameter an die Funktion g übergeben wird. Die Signatur von h besteht aus einem Parameter und dem Funktionsergebnis. Um nun das Aussehen des Parameters bestimmen zu können, müssen die schon gefundenen Signaturen von f und g zusammengefügt werden. Genauer gesagt muß ein Typ gefunden werden, welcher die Eigenschaften von g und von f berücksichtigt. Da das Ergebnis von f als Parameter für g dient, muß als erstes überprüft werden, wie sich der Ergebnistyp von f und der Typ des Parameters von g in Übereinstimmung bringen läßt. Es soll also ein gemeinsamer Typ für (a,[Char]) und (Int, [b]) gefunden werden.

f :: (a,Char) -> (a,[Char])
g ::             (Int, [b]) -> Int

Beide Typen, also (a,[Char]) und (Int, [b]), enthalten polymorphe Datentypen und lassen sich somit jeweils als Menge ihrer möglichen Ausprägungen darstellen. Wird über diese Mengen nun eine Schnittmenge gebildet, so ergeben sich daraus alle erlaubten Kanditaten für den gesuchten gemeinsamen Typ. Aus diesen Kandidaten wird nun derjenige herausgesucht, der die allgemeinste Form besitzt. In diesem Beispiel ergibt die Schnittmenge nur einen möglichen Typ und dieser (Int, [Char]) stellt auch das Ergebnis dar. Allerdings muß es sich nicht immer um monomorphe Typen als Ergebnis handeln, sondern auch polymorphe sind durchaus möglich.

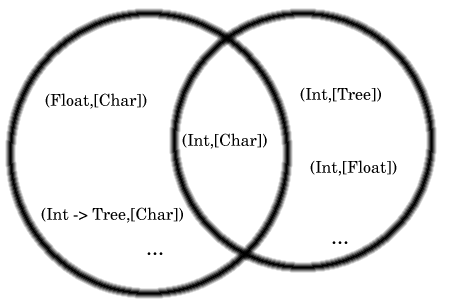
Dieser Prozess zum finden eines gemeinsamen Typs nennt sich Unifikation. Die Unifikationsalgorithmen, wie sie in Haskell vorkommen, sind allerdings weit komplizierter, und diese zu erklären würde den Rahmen dieses Dokumentes sprengen.
Nun ist bisher aber nur ein gemeinsamer Typ für f und g bestimmt worden. Aus diesem läßt sich aber nun der Parametertyp für h einfach bestimmen. Da der Parameter von f vom Typ (a,Char) ist und der Ergebnistyp von f schon auf (Int, [Char]) festgelegt wurde, folgt daraus, dass der Parameter von h den Typ (Int, Char) hat. Der Ergebnistyp von h muß derselbe wie von g sein, also Int.

h :: (Int, Char) -> Int

f :: t1 -> t2 -> ... -> tk -> t

f p1 p2 ... pk
  | g1     = e1
  | g2     = e2
  ...
  | gn     = en

• Jeder "Guard" gi muss vom Typ Bool sein
• Jeder Ausdruck ei muss vom Typ si sein, welcher wiederum mindestens so allgemein wie t ist
• Jedes pj muss vom Typ tj sein

Dieser Abschnitt soll klären, wie überprüft wird, dass Abhängigkeiten zu Klassen und Instanzen für einen Ausdruck korrekt sind. Als Beispiel wird die Klasse Eq mit ihrem == -Operator herangezogen und folgender Ausdruck, welcher diesen Operator verwendet:

member []       y = False
member (x:xs)   y = (x==y) || member xs y

Die Signatur wäre folgende:

member :: Eq a => [a] -> a -> Bool

e :: Ord b => [[b]]

Aus dieser Unifikation ergibt sich für member eine neue Signatur

member  :: [[b]] -> [b] -> Bool

mit dem Unifizierten Kontext (Eq [b], Ord b), der sich aus Eq [b] von der member -Funktion und Ord b von dem Ausdruck e zusammensetzt. Dieser Kontext muß nun soweit vereinfacht werden, dass eine passende Klasse für b gefunden wird. Der Kontext ist zuerst mit Hilfe der Instanzen der involvierten Typen aufzulösen. Aus Eq [b] läßt sich mittels

instance Eq a => Eq [a] where ...

nach Eq b auflösen, so dass sich als Kontext nun (Eq b, Ord b) ergibt. Diese Auflösung mit Hilfe der Instanzen ist solange durchzuführen, bis nur noch reine Typvariablen vorhanden sind. Sollten während dieses Auflösungsprozesses Typen auftauchen, welche keine Instanz zu Eq besitzen, schlägt die Typüberprüfung fehl. In dem Kontext (Eq b, Ord b) ist Eq b nun soweit vereinfacht, dass nur noch eine reine Typvariable vorhanden ist. Ord b muß gar nicht erst vereinfacht werden. Als nächster Schritt kann der Kontext zusammengefaßt werden. Aus der class-Deklaration wird ersichtlich, dass alle Typen, die von Ord eine Instanz besitzen, gleichzeitig auch eine von Eq besitzen.

class Eq a => Ord a where ...

Da wir eine allgemeinste Darstellung anstreben, wird der Kontext zu Ord hin vereinfacht. Er lautet nun (Ord b). Die fertige typkorrekte Signatur von member lautet also:

member e :: Ord b => [b] -> Bool