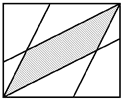
Gesucht ist die Zuordnung der einzelnen Vektoren des aufgenommenen Signals zu den Vektoren der Referenz. Dabei sollen bestimmte Regeln aufgestellt werden, da nicht jeder Vektor auf jeden zugeordnet werden darf.
Linearisierung der beiden Vektoren. Das heißt das Signal an einer bestimmten Stelle wird dem Referenzmuster an der entsprechenden Stelle zugeordnet.
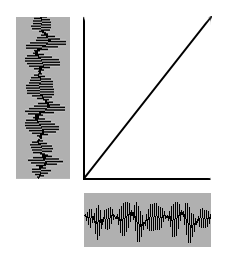
Dieser Ansatz kann unterschiedliche Sprechgeschwindigkeiten, die konstant über das ganze Wort sind, z.B. ein einfaches schneller Sprechen zuordnen. Er kann jedoch keine variierende Sprechgeschwindigkeit innerhalb einer Sequenz erkennen.
Gesucht wird also eine Zuordnungsrelation (keine Funktion), die xi auf yi abbildet, wobei jedem x mehrere y zugeordnet sein können (oder umgekehrt).
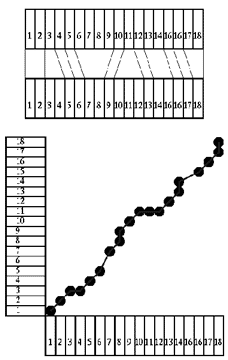
Die Wahl des am besten passenden Referenzmusters geschieht in zwei Schritten. Zuerst wird die bestmögliche Zuordnung des Signals zu jedem einzelnen Referenzmuster ermittelt, dann wird aus allen bestmöglichen Zuordnungen die beste ermittelt.
Die Zuordnung eines aufgenommenen Signals zu einem Referenzmuster wird dabei als Graph dargestellt. Für den Graphen werden nun, bildlich gesprochen, die Kosten berechnet, die entstehen, wenn das aufgenommene Signal auf das Referenzmuster abgebildet wird. Die Kosten ergeben sich aus folgenden Regeln:
Ermittelt werden zuerst die minimalen Kosten für die Zuordnung des Signals auf das aktuelle Referenzmuster. Durch die zweite Regel wird nicht zwingend die Diagonale zum günstigsten Pfad. Die Ermittlung der minimalen Kosten wird für alle Referenzmuster vorgenommen.
Im zweiten Schritt wird dann das Referenzmuster mit den geringsten Minimalkosten ausgewählt. Es entspricht dem wahrscheinlichsten Wort.
An den Graphen sind noch folgende Einschränkungen zu machen:
Der Algorithmus zur Berechnung des günstigsten Pfades ist in eine rekursive Folge einfacher Entscheidungen aufgeteilt. Für jeden Teilpfad wird der optimale Weg berechnet und am Ende rückwärts der Weg markiert (dynamische Programmierung).
Zur Vereinfachung werden

Das Verfahren ist auch anwendbar zur Anpassung von Referenzmustern, dabei wird eine zeitlich gemittelte Referenz aus zwei Referenzmustern gebildet.
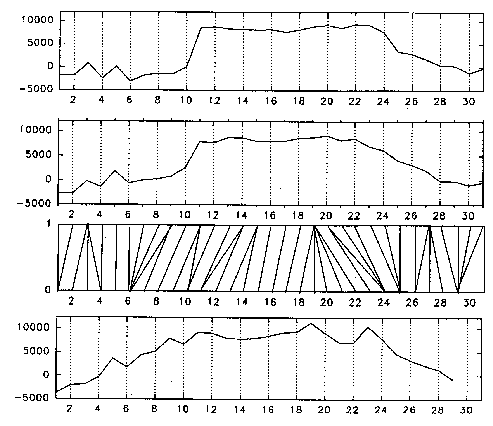
Die Abbildung zeigt die zeitliche Anpassungen einer Basisreferenz (erste Zeile) an eine zweite Referenz (vierte Zeile) mit den Blockzuordnungen des DTW auf dem optimalen Pfad (dritte Zeile), um eine gemittelte Referenz (zweite Zeile) zu erzeugen.
So setzt sich beispielsweise der Block 19 der neuen, gemittelten Referenz aus dem 19. Block der Basisäußerung und 5 Blöcken der daran anzupassenden zweiten Referenz zusammen.