Hidden-Markov-Modelle

• Probleme bei DTW
• Gewünschte Anforderungen an ein Modell
• Spracherzeugung als stochastischer Prozess
• Formale Definition von HMM
• HMM in der Spracherkennung
• Übergang Diskretes - Kontinuierliches Sprachmodell

Probleme bei DTW

Bei der Technologie des Dynamik Time Warp (DTW) bringt folgende Probleme mit sich:

• Zum Erkennen der Worte ist eine Endpunkt Detektion notwendig. Kontinuierliche Sprache ist also nur bedingt möglich.
• Es wird eine große Sammlung von Referenzmustern benötigt, da jede Wortform als Referenzmuster hinterlegt sein muss.
• DTW arbeitet nur mit einem sprecherabhängigen Modell, da alle Referenzmuster auf den Sprecher angepasst sein müssen.
• DTW erfordert einen hohen Berechnungsaufwand, proportional zur Vokabulargröße, da jede Referenz mit dem Gesprochenen verglichen wird.
• Durch ein großes Vokabular entsteht auch ein hoher Trainingsaufwand.

DTW ist also ungeeignet, wenn der Sprecher unbekannt und ein Training nicht möglich ist. Es ist außerdem ungeeignet für kontinuierliche Sprache. Es ist unmöglich, mit der DTW-Technologie unbekannte Worte zu erkennen, und schwierig, nur bestimmte Wortabschnitte zu trainieren.

Gewünschte Anforderungen an ein Modell

Aus den Problemen des DTW lassen sich die Anforderungen an ein neues Modell formulieren:

• Anstatt mit ganzen Worten soll mit Spracheinheiten kleiner als Worte gearbeitet werden. Dadurch kommt jede Spracheinheit häufiger vor, das Trainieren wird einfacher, die zu speichernde Datenmenge geringer.
• Spracherkennung soll Sprecher-unabhängig, ohne Training funktionieren, dafür müssen Sprecher-unabhängige Referenzen gespeichert werden.
• Spracherkennung von kontinuierlicher Sprache, dadurch müssen auch Wortsequenzen ohne erkennbare Pausen verarbeitet werden.
• Die Erkennung von nicht-trainierten Worten erfordert das Trainieren von Subworten und das Zusammensetzen von mehreren Subworten zu ganzen Worten (Vokabular-unabhängig).

Außerdem wird eine einwandfreie mathematische Grundlage gefordert.

Spracherzeugung als stochastischer Prozess

Um ein mathematisches Modell aufzubauen, wird die Erzeugung von Sprache als stochastischer Prozess angesehen.

Man geht davon aus, dass jedes Wort bzw. Phonem bei jedem Aussprechen anders klingt. Weiterhin kann man Worte bzw. Phoneme oder andere Sprachteile als Zustände eines Spracherzeugungsprozesses annehmen. Von einem gegebenen Zustand kann man nun verschiedene Laute erzeugen, also neue Zustände erzeugen. Es sind jedoch nicht alle Zustandsübergänge möglich.

Man kann außerdem davon ausgehen, dass ein Spracherzeugungsprozess entsprechend einer bestimmten Wahrscheinlichkeit bestimmte Laute erzeugt. Bestimmte Lautübergänge erhalten höhere Wahrscheinlichkeiten (auf "e" folgt "r"), andere erhalten geringere Wahrscheinlichkeiten (auf "n" folgt "f"). Der Erzeugungsprozess vollführt also Übergänge von einem Zustand zu einem anderen

Ein Sprachmodell besteht folglich aus Wahrscheinlichkeiten für die Lauterzeugung und für Lautübergänge.

Formale Definition von HMM

Zur formalen Definition von HMM unterscheidet man zuerst zwei Mengen:

• Die Menge von Zuständen S:{s₁, s₂, ..., s_n}, die alle Subworte bzw. unterscheidbaren Laute umfasst.
• Den wahrnehmbarer Merkmalsraum V, der entweder diskrete Werte annehmen kann (V={x₁,x₂...,x_v}) oder stetige (V = R^d). Im wesentlichen werden jedoch stetige Merkmalsräume verwendet.

Außerdem werden verschiedene Wahrscheinlichkeiten unterschieden.

• Die Initial-Wahrscheinlichkeits-Verteilung p, wobei p(s_i) die Wahrscheinlichkeit ist, dass s_i erster Buchstabe einer Sequenz ist.
• Die Matrix der Zustandübergangs-Wahrscheinlichkeiten A=(a_ij), wobei a_ij die Wahrscheinlichkeit ist, dass der Zustand s_i in den Zustand s_j übergeht
• Die Menge der Ausgabewahrscheinlichkeiten B={b₁,b₂...,b_n}, wobei b_i(x) die Wahrscheinlichkeit ist, dass im Zustand s_i das Merkmal x ausgegeben wird.

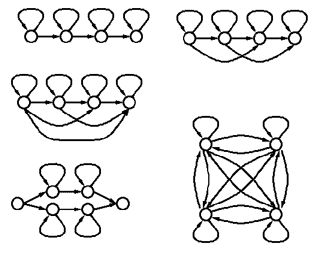
Die Abbildung zeigt verschiedene denkbare HMM mit Übergängen.

HMM in der Spracherkennung

In einer Trainingsphase werden bestimmte lautliche Einheiten (Phoneme oder Wortteile) als an den Sprecher angepasste Hidden-Markov-Modelle gespeichert, diese werden auch Allophone genannt. Jedes Allophon enthält bis zu acht Zustände. Außerdem erhalten die Zustände bestimmte Anfangs- oder Endwahrscheinlichkeiten, also Wahrscheinlichkeiten, dass das Modell am Anfang oder Ende steht.

Die zeitliche Variation der Aussprache wird über eine Selbstreferenz hergestellt, das heißt, dass ein langgesprochener Laut (Zustand) auf sich selbst abgebildet wird und dadurch im Modell verlängert wird.

Für jede Einheit (Wort) wird mit dem HMM die Wahrscheinlichkeit berechnet, dass das gespeicherte Modell (Folge aus Zuständen) das aufgenommene Signal erzeugen kann.

Da die Berechnung für jedes Modell durchgeführt werden muss, kommt es zu einem hohen Rechenaufwand. Um ein HMM für ein Wort mit n Phonemen und der Länge T vollständig zu berechnen müssen 2·T²·n Berechnungen durchgeführt werden.

In der Praxis kürzt man diese Berechnung durch spezielle Rechenverfahren ab. Dadurch wird die Berechnung ungenauer, aber schneller.(Algorithmen: Viterbi-Algorithmus, Forward-Backward-Algorithmus, Baum-Welch-Optimierungs-Regeln).

Viterbi- und F/B-Algorithmus arbeiten vergleichbar dem DTW rekursiv mit Teilwahrscheinlichkeiten, das heißt, sie berechnen erst alle Wege das Ziel abzubilden, dann den wahrscheinlichsten.

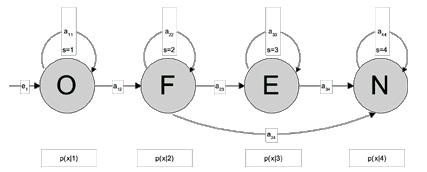
Die Abbildung zeigt ein sehr simples HMM (nur ein Zustand pro Laut) für das Wort Ofen. Die Verlängerung der einzelnen Vokale wird durch die Selbstreferenz verdeutlicht ("Ooohfen"). Außerdem ist es möglich, aus dem "f" direkt zum "n" zu gelangen, wie es umgangssprachlich häufig vorkommt ("Ofn").

Übergang Diskretes - Kontinuierliches Sprachmodell

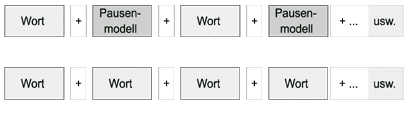
Über eine Veränderung der HMM wird das Erkennen einer kontinuierlichen Sprechweise ermöglicht. Das war bisher durch die relativ schwache Rechengeschwindigkeit nicht möglich. Daher erwartete das HMM nach jedem Wort ein Pausenmodell. Mit gestiegener Rechengeschwindigkeit lassen sich größere (längere) HMM berechnen, ein direkter Übergang der Modelle wird dadurch möglich.