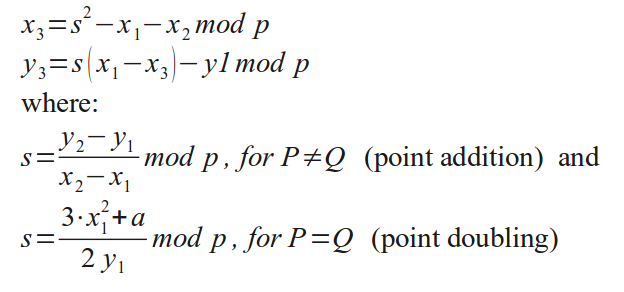->back to Academic Signature home
Manual
for Academic Signature
An open source program for
elliptic curve cryptography
(digital signatures, ciphers, timestamps)
written by M.Anders,
status April 2017
This manual is about how to use Academic
Signature for digitally signing documents, the context in
which to use it and some important basics of cryptography.
It is not about explaining the menu options.
1 Purpose and
Scope
Nota Bene:
In spring 2013 the Snowden revelations about abusive and
persistent privacy intrusion by US and UK governement
agencies(aided by the german BND) gave a surprising new
importance to the enciphering options in Academic Signature.
I didn't anticipate that and had initially regarded
enciphering as a free addon to the technically more
challenging authentication schemes.
It so happened that nowadays my software seems to be
primarily used in self-defense for encryption.
The logs reveal that most downloads go to North America,
many to Germany, France, Russia and untraceable proxies(well
done!), some into remaining Europe, a few to Asia and almost
none to South America. Lately computers in some asian
countries(e.g. Malaysia, China or India) became active
downloaders.
This usage is necessary due to what I consider being apoor
job of our politicians in protecting the freedom and privacy
of the population they were elected to care for.
Consequently in 2013 I began to use Academic Signature
additionally for encryption of the communication with
partners in industry. If we exchange information about the
assessment of work done by our students and the appropriate
grading, we cannot allow nation state secret agencies to
collect and evaluate sensitive personal data or company
secrets to illegaly fill their cabinets with.
The remainder of this manual relates to authentication.
In my teaching position at a university(University of Applied
Sciences Wedel / Fh-Wedel) I am frequently asked by students to
write letters of recommendation for job applications, applications
for entering curricula at other institutions, applications for
scholarships and the like.
The project Academic Signature was
initialized unwillingly by a large german organization giving out
scholarships. They gave me a form(needless to say “paper”-form) to
write the letter of recommendation into and I was supposed not to
write by hand but to explicitly use a “typewriter” instead (year
2010! Can you believe it?), sign the form, put it into an envelope
and send it to them. This was definitely enough! So I decided to
develop “Academic Signature” and finally get us into the 21st
century. The primary purpose of Academic Signature is to serve as
a drop in replacement for this 19th century
process.
Please note, that the proposed use of Academic Signature for
authentication of academic documents and the respective public keys
in the academic community(or other communities) is substantially
different from the fully anonymous community use, the standard PKI(Public
Key
Infrastructure) is intended for. Standard PKI tries to
establish a continuous “chain of
trust” reaching from a single central authority(the
government or the big software vendor that finally wins the race)
into the branches to you and me. This structure would be well suited
for electronic signatures and communication if set up properly.
Another distinct model for trust
management is the “web of
trust” employed e.g. by PGP, where communities of
trusting friends connect to form a web of connections. This setup
allows for individuals that don't know each other, but are
connected by a thread of trust via shared trusted friends, to
communicate confidentially. Digital signatures are of limited use
in this web of trust, because to my knowledge no individual
information about the partner you are communicating with other
than composition of the public key and strength of trust
connectivity is transferred.
Academic Signature works in a “mosaic
of
trust” that forms in a semionymous(somewhere between onymous and
anonymous) community
like e.g. the academic community, the community of soccer team
managers and trainers, the Beatles web-fan-page maintainers or the
like. It is essentially the mosaic of trust we have been used to
rely on paperbasedly in daily life for centuries, long before the
advent of the computer. In essence the digital signature created
with "Academic Signature" is logically equivalent to the medieval
leaden bulla of the pope or nowadays the poor man's physical
signature in ink. It has to be accompanied by additional
information from other parallel channels.
If we get a physically signed letter
of recommendation from a colleague, we usually don't even know and
recognize the signature itself. We memorize having read a paper
from the colleague, maybe we have seen her at a conference, we
check for professional paper and letterhead from her affiliation,
we read the text and recognize whether it sounds professional or
could have been written by a student(->the "semantic test").
And if in doubt we finally make a phone call.
This typical state of affair can be
substantially improved, if a digital signature is used instead of
the ink signature. Transferring the letter can be sped up to
seconds, the student does not need to get notarized copies of the
letter to supply several applications, forgery of the digital
signature is overwhelmingly more difficult. But keep in mind: The
other components of the mosaic of trust must remain in place and
maybe be amended for the modern techniques. You might have not met
the colleague personally but may have skyped her, you perhaps did
not visit her lab but inspected her website and considered it
professional, you may not inspect the watermark of the letter
paper but make sure the colleagues website offering the public key
is embedded in the right, serious university web appearance. And
if in doubt, you still pick up the phone.
Please note, that two of the above
mentioned models of trust(web/mosaic) ultimately deal with
interactions between people and trust between them.(The chain of trust,
exclusively relying on cryptographic protocols without direct
human involvement and relying on the integrity of a central
authority is best suited for interactions between software/net
entities and is the only model of trust that may operate -or go
nuts- in the background without user awareness or control).
So the mosaic of trust is not primarily a concept of "IT-security"
but of security in general everyday life. Thus Academic Signature,
relying on the mosaic of trust, is not an entity of "IT-security"
but a standalone IT-tool having the potential of serving and
enhancing general security in everyday professional communication.
Using Academic Signature requires
computer literate users with security awareness. The user should
know the very basics of public/private cryptosystems(preferably
even of elliptic curve cryptosystems) and the user be it signer,
messenger or prover must understand, that Academic Signature used
with the protocol described below is a faster, more secure and
more efficient drop in replacement for the traditional ink
signature. Not more and not less.
It can be regarded as a second
generation intellectual empowerment for authentication. In former
times the first generation was also established in a small
semionymous community: Those few who could write could sign. Now
those who can competently use asymmetric cryptography, can sign
digitally.
->
back to content list
2
Guiding Lines for Program Design
Some established guiding lines for
the design of cryptographic software are:
a) The user is cryptographers main security risk
and has to be protected from degrading security by inventing
reckless shortcuts. Automate anything that can be automated,
reduce risky user interaction to a minimum.
b) Give as little as possible options, show as
little as possible information.
c) Never invent anything, stick to approved,
certified algorithms.
d) The users (and the buyers) of cryptographic
software have no interest in the internal logics of
en/deciphering or signing. They want to trade money for security
and not stress their brains.
This may certainly be a valid and
well suited approach for banking software (and software for
bankers for that matter ;-). It is certainly not a philosophy that
nurtures progress. For me it can certainly not be the guiding line
for an academic and computer literate environment (or generally a
computer literate environment). So I had to violate them all:
a) The user
will only accept employing digital signatures if he/she is
enabled to understand what he/she is doing and only if he/she
has manual control
over each single step in creating the signature and
releasing it to the public (or withholding it at the
last second for double checking). The user is as responsible in
applying the signature software as he/she is when signing a cell
phone contract, a cheque or when shopping with the credit
card(hopefully even more so). Academic Signature will not
attempt to protect the user against what might be presumed
ignorant or risky behavior. I consider this a matter of respect
towards the user.
b) Transparency is an important prerequisite to
make users acquainted with modern digital authentication and use
it responsibly. So upon request Academic Signature shows the
domain parameters, exports public keys in human readable form,
shows private and public keys in plaintext (hex-notation),
allows to import external public keys by text based copy and
paste from websites or other documents into the respective
dialog fields, sticks to the naming convention used in the
cryptographic literature, .....
c) I couldn't care less. Hey, I am a physicist
and work in the education business. I do this for fun(eating the
dust of Windows7 made me entertain some doubt though). Reading
standards documents amassed by some committee or copying
established algorithms is no fun. So I invented my own random
number generator, hash algorithm and symmetric en/deciphering
("Dancing Fleas"). Unfortunately I was not able to invent a
secure new asymmetric algorithm, but at least Academic Signature
uses an advanced/modern one. And - seriously - the
cryptographic scene is in danger of loosing some "Biodiversity".( I included the
NIST-approved hashes "SHA256", "SHA512" from the SHA2 family and
the symmetric algorithm"AES", which is the only code I didn't
write myself but instead took from the "polar ssl"-website. Lately I additionally
included Hongjun
Wu's finalist "JH" from the SHA3 competition to the
collection of available hash functions. Hongjun's C-code was
directly incorporated into Academic Signature.)
d) The user is striving to understand what
she/he is doing and why(even on the computer and even on a
windows-os) and goes through life with a curious mind. In my
opinion everyone should adhere to that principle in any case,
anywhere at any time.
There are only few alternate domains
supplied with the Program. This is to promote transparency for
novice users and ease compatibility towards older versions of
academic signature.
There is, however, a domain dialog for handling use of multiple
and distinct domains. The advanced user will be able to go e.g. to
a 512 bit domain by researching how to create a new domain(not
trivial) and/or import it (see e.g. http://www.ecc-brainpool.org/download/Domain-parameters.pdf
where I got some domain parameters from). It is also possible to
import and use the NIST-Domains. You have to watch out though -
there may be some copyright protection of the NIST-Domains in some
countries and you should make sure to use only domains larger than
230 bit. Domains of smaller bitsize may become insecure over the
next decade.
Lately I created and posted additional ec-domains of substantially
larger bitsize than the NIST or ECC-Brainpool domains myself. You
get them here.
Furthermore, the current version of academic signature supports
cross domain operations and you can e.g. sign a document with a
key from a 1033 bit domain and encrypt it for a recipient using a
public key of say a 640 bit domain with one mouseclick.
-> back to content
list
3
Basics of Public Key Cryptography
see also: http://en.wikipedia.org/wiki/Public-key_cryptography.
One type of mathematical function is
a core necessity to establish Public Key Cryptography. You need a
so called commutative "Trapdoor One-way Function".
A one-way function is a
function that can be efficiently applied to an argument(i.e. it
can quickly be evaluated) but which cannot efficiently be
inverted. It would take excessively long to find the argument if
you are only given the result. Exponentiation in a prime
field(= modulo a large prime) is an example for such a function (
i.e. the mother of all such functions, the inverse function
coining the name "Discrete Logarithm").
f(a,p,x) = ax mod( p)
There are more mathematical
functions with these properties and nowadays the hard problem of
inverting such a function(i.e. finding x for given a, p, f(a,p,x))
is called the "Generalized Discrete
Logarithm Problem" ( or the generalized DL-Problem).
Application of the one-way function may be commutative like in the
above mentioned case:
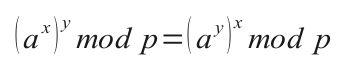 Onewayedness
and commutativity of the function application are sufficient to
perform a so called Diffie-Hellman
Key exchange and the so called elGamal encryption.
Onewayedness
and commutativity of the function application are sufficient to
perform a so called Diffie-Hellman
Key exchange and the so called elGamal encryption.
For creating and verifying digital signatures the function
additionally needs the "trapdoor
property". Knowing a secret, and only knowing this secret, the
function can be inverted. The secret here is knowledge of the
discrete logarithm x, which renders inverting easily possible(if working within a subgroup
of prime order).
3.1 Asymmetric
Encryption/Decryption
Asymmetric encrypting is performed with a publicly known key of the
recipient.
1.) The plaintext is enciphered using a symmetric algorithm e.g. AES
or Dancing
Fleas (the one I am using for securing keys in Academic
Signature).
2.) Then the key is enciphered with an asymmetric algorithm e.g. RSA or an EC variant
of elGamal, using the public key of the recipient. The encrypted key
is attached to the ciphertext document and all is sent to the
recipient. The recipient splits enciphered key information from the
symmetrically enciphered ciphertext and reconstructs the key using
his/her private key. Only the targeted recipient can invert the
encryption and reconstruct the key. (Only the recipient knows the
"trapdoor secret". The "trapdoor secret" is the private key
corresponding to the publicly known "Public Key".)
Finally the recipient decrypts the ciphertext using the recovered
key.
3.2 Signing
see also:
http://en.wikipedia.org/wiki/Elliptic_Curve_DSA
Digitally signing a file means performing a mathematical operation
on a secure hash-value
of
the file, that can only be done in reasonable time(before the sun
goes red giant and swallows earth) if the secret is known to the
signer. Everyone who knows the public part of the key can quickly
verify, that the file was signed by the holder of the secret i.e.
the private part of the key, but cannot sign.
The operations necessary for signing and verifying are somewhat more
involved for DSA and ECDSA than just inverting the trapdoor one-way
function in the above example and involve use of ephemeral keys.
(They are extremely simple
in the RSA-system though - just encipher the hash with the private RSA key.) The steps can
be seen in detail for the ECDSA system here.
In brief: You perform a calculation involving a unique and secret
ephemeral key and your permanent private key. This calculation
involves an equation featuring a product of the inverse of the
ephemeral key ke, a publicly known signature component "r", your
private key and other non secret terms (including the hash value of
the document). As long as it stays being one equation with two
unknowns(to the public), it is safe. If an attacker gets knowledge
of the ephemeral key(or if the same one is used twice and the
attacker suspects that) the equation has one unknown left(on ke
reuse two equations with two variables) and is easily resolvable by
the attacker to get hold of your private key with catastrophic
consequences.
Thus good random numbers are of utmost importance for safe ECDSA (or
classical DSA) signing. Academic Signature supplies the "Dancing
Fleas RNG", which is primed on hatching, re-randomized every now and
then during program execution and whose state vector on exiting is
stored with cryptographic protection.
Please note that in sophisticated attacks on DSA or ECDSA, the
random number generator is a prime target (and has been in the
famous break of the ****-game console recently). To my knowledge,
standard bodies have not endorsed a specific RNG yet and different
creations(like e.g. Dancing-Fleas-RNG) are in use today.
Please note that some software vendors offer products for ECDSA
signing that install without proper initialisation of a Random
Number Generator and do not disclose how their ephemeral keys are
produced. A proper RNG-initialisation on a standard computer would
always be visible to the user, e.g. asking for some arbitrary mouse
movements or an ephemeral picture-file created by the user on
installation of the software. So if you happen to own such a
product, do not rely on it for serious matters.......
3.2.1 Professor Smart, Dr Honest,
Professor Veryrich
Professor Snake, Dr Mallory, Professor Vain
The cryptography literature uses a lovely naming convention. The
protagonists Alice and Bob ( "A" and "B") want to
communicate securely, eventually with the aid of the trusted
authority Trent. Eve is trying to listen in and Mallory or Oscar attack the system, try to
get hold of the keys and/or forge and alter messages. Since I
enjoyed this while reading cryptography texts, let me introduce
similar protagonists and antagonists:
Professor Smart (S=Signer)
is the signer wishing to do all the best for his/her students. The
testimonial is about Dr Honest
who will honestly forward testimonial and signature along with
his/her application to Professor
Veryrich (V= Verifier) who admits to a curriculum or hires
research or teaching assistants for the sole purpose of advancing
academic knowledge and helping Dr Honest to get along with his/her
career.
Occasionally there will antagonists be involved:
Professor Snake may out of
jealousy or rejected love try to discredit Dr Honest or Professor
Veryrich by giving out faulty signatures, Dr Mallory may try to forge a testimonial to her
advantage and Professor Vain
may maliciously discredit Dr Honest or Professor Smart out of
jealousy or as an attempt to hide his illiteracy in computer
matters.
These participants will be on stage in the later paragraphs on the
security of Academic Signature.
-> back to content list
4 The Secret in
the Elliptic Curve Cryptosystem(ECC) “Academic Signature”.
see: http://en.wikipedia.org/wiki/Elliptic_curve_cryptography
or my summarizing text below....
The ECC in general is based on the
hard problem of finding the secret factor "x" in the operation "point
multiplication" of a publicly known Point "D0" on an
elliptic curve, that leads to the published resulting Point "A".
x * D0 = A
The operation "point multiplication"
is the Trapdoor one-way function that is commutative and can only
be inverted if the secret x is known (and if additionally the point operations are
performed modulus a large prime p, leading to large known! prime
group order q). This point multiplication is logically
equivalent to the exponentiation in the example from paragraph 3.
In an ECC "x" is the
private key, A is the
public key and D0 along with other
domain parameters are publicly known and must be agreed on before
the cryptographic interactions at hand.
4.1 Elliptic Curves
see also(in German) : http://www.ecc-brainpool.org/ElliptischeKurven_und_Signatur_Studie.pdf
An elliptic curve(!not an ellipse!) can be described by the
equation(->Weierstrass form):
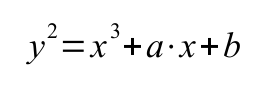
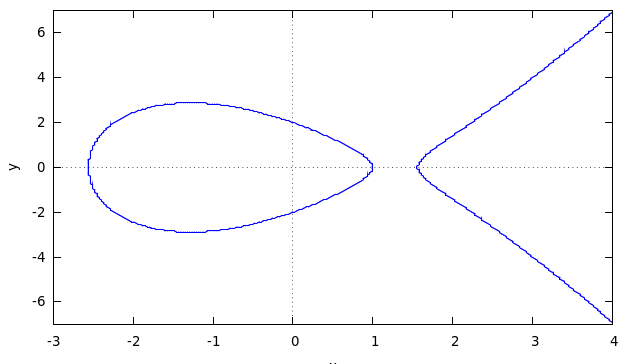
The figure below shows a curve over real numbers with parameters a=
-5, b=4 (Plot was generated by wxMaxima,
the
left part may or may not appear as a separate bubble depending on
curve parameters a, b)
Point addition is a method of constructing a third point on the
curve from knowledge of two and is defined graphically in the figure
below:
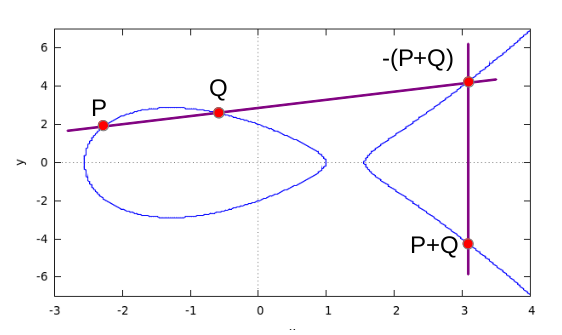
The "sum" of Points P and Q is the intersection of a line through P
and Q with the elliptic curve, mirrored at the y-axis. You get the
negative of a point on the curve by inverting the y-coordinate. Or,
to state it in an alternate way: The point-sum of three
intersections of a straight line with the curve is 0.
Graphically the definition extends smoothly to the case of P=Q,
where the straight line is a tangent to the curve at P and the
intersection is P+P=2*P, the doubled point. For mathematical reasons
you have to include the point (0, infinity) as neutral element of
addition.
Casting these definitions into algebraic terms results in the
following equations:
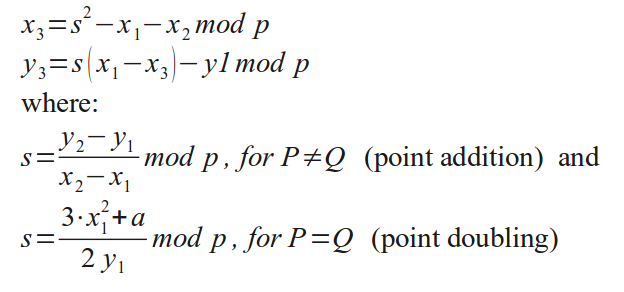
The calculations performed in real numbers are of no use for
cryptography, so they are performed for large integer numbers modulo
a large prime p. In this case, the "curve" is transformed into an
unpredictable scatter of points in the x-y-plane of integer numbers.
Please note that point multiplication with a large number now
involves a "large number" of large integer divisions, which are very
slow to evaluate. In order to get tolerable execution times, you
have to switch to some version of so called "projective coordinates"
to replace the divisions by multiplications.
As in exponentiation used in the classical DL-problem (e.g. in
classical DSA)
point multiplication can be performed in the usual way by chaining
shifts and additions(add(ECDSA)/multiply(DSA)
shifted value if the corresponding bit in the factor(ECDSA)
or exponent(DSA) is 1).
4.2 Domain Parameters
Domain parameters -the "stage on which calculations are
performed"- are the prime module p used in the classical
algebraic operations and the curve parameters a and b and a selected
primitive point "Do" which generates a group of prime order "q".
Academic Signature has a menu entry "elliptic_domain -> domain
dialog" allowing the user to inspect the currently used parameters
a, b, p, Do (and resulting q) and to perform numerous other
operations on domains.
For creating a signature(or for decryption), the trapdoor function
(here: point multiplication) must be invertible for the holder of
the private key. This is not possible for arbitrary combinations of
prime moduli p, curve parameters a and b and primitive point Do. One
way to achieve invertibility is to choose a combination of p, a and
b such that the points using the operation point
multiplication/addition mod p based on primitive point Do result in
a group of points of large prime group order
"q". In this case the inverse of a known integer factor in point
multiplication(e.g.the private key) can be found efficiently with
the chinese
remainder
theorem(="Chinesischer Restsatz" in german).
To find such domain parameters that result in (large) prime group
order q is a difficult task. Determination of the group order alone
is calculation intensive already. It is determined with the Schoof-Elkies-Atkins
algorithm. Then try until it is a large prime close to p. If
you want to create a domain yourself, you may e.g. use the "miracl"
tool published by Shamus Software
Limited. It is free for non commercial use and can be
downloaded from here.
Luckily this is about the only really calculation intensive task in
ECDSA and we can use domain parameters published by trustworthy
noncommercial organizations. NIST
, ECC-brainpool
or my humble self -> my_domains
are sources of such domain parameters .
To sum it up: In
the case of elliptic curve cryptosystems (ECC) the very hard
part is finding an appropriate
domain ) - (the problem is non existent for RSA and of medium
difficulty for elGamal and DSA) whereas the
generation of private/public key
pairs is laughably easy for
ECC ("babyeierleicht" as my son would call it). (for comparison: It will take your computer
some minutes to create a strong RSA key, it is easy for
elGamal and classical DSA also).
4.3 Private Key
The private key is an arbitrary number slightly smaller than group
order q usually denounced "d".
Impatient
people may precalculate the inverse of d to save a split second
later on for signing. Academic Signature calculates this value on
the fly only if needed, using the chinese remainder theorem and
discards it after usage.
Academic Signature will suggest appropriate random numbers or you
can type the key yourself into the corresponding field in the key
generation dialog to add some personal flavor.
4.4 Public Key
The public key, usually denounced "A",
is
the point product A
= d * Do. (red
stands for secret information, green for public information)
Others cannot calculate d from A in reasonable time, this is a
hard generalized DL-Problem.
A potential communication partner can
multiply your public key A with a random number "ke"
he/she selected to get "B" B = ke * A (= ke * d * Do)
, and keep B secret. Simultaneously the communication partner
calculates "C",
C = ke * Do
and broadcasts it to you.
No third party can recover ke or B but you can reconstruct the shared
secret B
by multiplying C (= ke * Do) with
your private key d. If your communication partner selected -say-
the x-component of point B to symmetrically encipher a message
with, you are able to decipher it since you can
reconstruct the key. This procedure is the ECC version of elGamal
asymmetric encryption or -if symmetrisized- ECC Diffie-Hellman
key agreement. Please note that the trapdoor functionality
is not needed for these cryptographic protocols, commutativity
in applying the one-way function suffices.
If trapdoor functionality is in place and you can invert point
multiplication with your private key, creating and verifying
digital signatures is also possible This can be done using
classical DSA
with the simple example from chapter 3 or, in this case, it is
called ECDSA
(= Elliptic Curve Digital Signature Algorithm)
Employing the ability to invert point multiplication, other
versions of enciphering are also possible:
Others could multiply your public key A
with a random number "ke"
they selected to get "B"
and tell you B = ke * A,
while simultaneously calculating C = ke * Do and keeping it
secret.
No one can recover ke but you
can recover C by multiplying B with the inverse of your private key d
and share this secret "C"
with whoever sent you B. This again opens the possibility to
communicate securely or to encrypt asymmetrically.
Obviously in all cases, you'll have to publish the domain
parameters along with your public key A(and the exact procedure
used for symmetric enciphering or hashing) to allow for
non-ambiguous calculations in all these cryptographic
procedures.
-> back to content list
5 The
“Protocol”, User Obligations
and Etiquette
In the following three subchapters,
a special protocol for using Academic Signature is presented,
which involves the subject of the testimonial. This protocol is of
the broadcast type, where the sender/signer disclaims control over
who is going to receive the testimonial. I advocate to use this
protocol, because it will produce a benefit for all protagonists
involved.
Academic Signature could be used in
a different protocol without the involvement of the testimonials
subject, where the content is concealed from the testimonials
subject and the prover communicates directly with the signer. I
consider this variant marginally unethical and disapprove of using
Academic Signature for this variant. A logically sound
implementation of this alternate protocol involves public signing
and encryption, which is possible with academic signature. But
using this type of protocol technically would aggravate the
testimonials subjects(=the students) situation. I disapprove of
this use and favor openness - please stick to the original
protocol!
5.1 Signer Obligations
The signer is the person who writes
and signs documents (i.e. letters of recommendation,
testimonials,...). Naturally the requirements for computer
literacy and responsible conduct are higher than for messenger or
prover.
-
Signers utmost duty is to
protect his/her private key. Everything else is of lower
priority. If a key has been compromised, this has to be posted
on the signers webpage and the key has to be blacklisted.
-
The signers duty is furthermore
to post his/her public key(s) together with contact
information preferably on a protected corporate/university
website. The website should also show the signers professional
position to allow provers to assess the significance of the
signature.
-
Signers should keep a file of
all documents signed and it is recommended, that a
conventionally signed paper version is also handed out to the
messenger.
-
Under all circumstances signers
must carefully read what they sign. It is strongly advised
that signers sign only documents they have personally
produced.
-
The signed document should
contain a header and/or footer with the information that it
was digitally signed, where to get the public key of the
signer, correct date, place and name of the signer (as in a
conventional signature).
-
The signer is advised to sign in
a "ceremonial" quiet atmosphere, preferably office doors
closed, certainly in the absence of the messenger. He/she
should never ever leave the computer while logged into
Academic Signature (-> see the coffee break office ambush).
Immediately after finishing work with Academic Signature, the
program should be closed.
-
If a private key is phased out,
the signer is responsible for physically deleting the private
key. The public part should stay visible to the public, if the
key has not been compromised, to allow for future
verifications.
For demonstration purposes I created an example testimonial and the
corresponding signature.
5.2 Prover Obligations
The prover is the person who has to
decide about admitting the applicant to a curriculum, hiring
him/her as research assistant etc. The provers obligations are
naturally less extensive than the signers. Additionally, the
interaction of the messenger with the prover is less intense, than
interaction with the signer. Cheating by the messenger is much
harder and thus less likely to be attempted on the provers side
compared to the signers side.
-
First, the prover reads the
presented document carefully and decides if a verification of
the document is at all necessary.
-
If the prover doesn't feel
sufficiently computer literate and needs to prove, he/she
doesn't hesitate to ask for a conventional version or phones,
skypes or emails the signer for informal verification.
-
A computer literate verifier
downloads and installs Academic Signature(if not already
present) according to the procedure given in section 6.
-
The prover gets the public key
from the website indicated in the documents footer. The prover
carefully and thoroughly assesses the credibility of the
website and the pages it is embedded into(or the alternative
source) and additionally assesses the significance of the
signers judgment regarding the messenger. This is the step of
utmost importance on the provers side.
It is advisable to locally store the external public key and
e.g. retain the key in the protected Academic Signature depot
file.
-
The prover uses Academic
Signature to verify the signature.
-
In case the verification fails,
technical failure or human error, not forgery by the messenger
is to be considered the most likely cause. The prover
subsequently contacts the signer, informs about the
verification failure and inquires about the correctness of the
contents of the testimonial.
5.3 Role of the Messenger
The messenger is the person who
transports the document plus signature file from signer to prover
and is also the subject, the document is about. In crypto terms
he/she is the “insecure channel”. Naturally the messenger has the
means(and the right) to skip the protocol altogether and throw the
message away.
The messenger is the participant with the highest possible gain
from fraud and therefore is not involved in signing and verifying.
She/he is physically absent during these procedures. There are no
obligations for the messenger in this “protocol”, but the
messenger has certain rights in the protocol at hand.
-
The messenger receives the
document file containing the testimonial and the respective
signature file and -if considered favorable- transfers them to
the prover. He informs the prover about the presence of a
digital signature and hints at the verification procedure.
-
Upon request by the prover, the
messenger supplies a classically signed paper document -no
questions asked -no rolling eyes.
-
The messenger has the right to
keep the document confidential and not show it if he/she
considers the content unfavorable.
-> back
to content list
6
Installation and setup
6.1 Preparation of a Protected
Domain on the Harddrive
For added security, prepare a
cryptographically protected drive (e.g. using Veracrypt) and create
an empty directory. Unzip the downloaded archive into this
directory. Newer versions of Academic Signature also exist as
windows setup files, which automatically install the crypto
software and place icons to the appropriate places. During
execution of Academic Signature, less sensitive parts of
keys(name, id, public components) reside temporarily in a
plaintext file and in plain form in memory. Remains of deleted
files have protection if the files were residing in a
cryptographically protected disk domain.
The problem of memory containing
confidential data being swapped to hard disk, which then may not
be physically wiped, stays though and is out of my(=the program
developers) control. From version(40) on, accidental transfer of
sensitive information(password, private key, RNG-content) to the
hard disks swap is prevented. For extremely high security, used
hard disks must be guarded and burnt under surveillance for
disposal - but let's not get carried away here.... after all we
are talking about letters of recommendation for students and not
US-government embassy reports.... :-))
6.2 Hatching
Academic Signature adheres to the
hatching duckling model for installation. If called for the first
time, it is in a vulnerable state and the sensitive files are
protected with the keyword "default". Then to imprint your
exclusive access it asks you for a passphrase, to immediately
protect your sensitive data with. The passphrase -of course- is
not recorded. If you forget it, all key information is permanently
lost, which includes your private key(s).
In a further step the "Dancing
Fleas" Random Number Generator(RNG) of 2011 byte
length is initialized from a file. You will be asked for a file,
that no one else has access to e.g. a picture of you which you
just shot with your webcam or a letter, which you never sent. For
added security, you may opt to delete it afterwards. Academic
Signature digests this file and uses it for initializing the
"Dancing Fleas" RNG. Later you can refurbish the initialization
anytime by mixing in an arbitrary phrase (Menu-> File ->Seed
....). Your actions during program execution also influence the
development of the random number pool. Thus the "Dancing Fleas"
RNG will never reproduce numbers even if seeded with identical
initializers. The state of the RNG is stored on hard disk with
cryptographic protection. This facilitates higher safety for
private key generation at a later stage.
In the initial state, the keyfiles
include a dummy key(private and public) for playing around with
and my public key, which I used to sign the binaries with.
Generation of cryptographically strong keys takes a split second.
They gain value by your act of using them. As long as they haven't
been used and the public part is not published, they can be
deleted without second thought.
6.3 Proving the Integrity and
Authenticity of Academic Signature
As a first exercise you are advised
to check the signature of the program itself. The executable's
signature is the file with identical name of the executable with
the additional extension ".ecsg" (=Elliptic Curve SiGnature). I
signed it with my private key. (My public key is already in store
after hatching for warmup exercises). The public key should be
taken per copy and paste from my webpage https://www.fh-wedel.de/~an/crypto/academic_signature_key.html
after assigning the trustworthyness of this site by checking e.g.
the proper embedding in Fh-Wedel's official web-appearance.
The key is also present on the website in form of a human readable
file, which can be imported into
Academic Signature.
Basically the public key consists of
two coordinates of a point in the plane(Ax, Ay). It is valid in
the context of certain "domain parameters", describing a specific
elliptic curve. For simplicity I included a standard domain with
256 bit keylength (comparable
in security with a 3072 bit RSA-Key - banking applications
mostly use RSA-2048 most others 1024, this webpage from Fh-Wedel
is protected against hacking with 1024-bit RSA, the self issued
certificate shows that the key expired in June 2009, which is no
problem if the certificate is self issued anyway ;-).
The parameters of this default domain were taken from from
ECC-brainpools website (http://www.ecc-brainpool.org/)
where you can also find information on ECC security.
Depending on your system speed,
verification may take some seconds, the main time being used for
generating the hash of the executable. (The elliptic curve
operations themselves take a split second even for the largest
domains of 1024-bit or more.) If you would want to sign a movie of
1 GB, you'd have to wait for some minutes ;-). But remember,
changing one bit of the gigabyte somewhere will completely change
the hash value, and this has to be achieved in a cryptographically
secure way.
I do admit that there are faster hashes than the newly introduced
algorithms of the "Fleas" family. (If this is a major problem for
you you should use the sha options). And if I knew how to speed
"Fleas" up safely, I would. But to reduce your annoyance I
should mention that faster hashes are inherently more susceptible
to “brute force attacks”(http://en.wikipedia.org/wiki/Brute_force_attack).
Verifying the Linux binary should take about 1 second, under
windows you will need about 2 seconds to verify. The elliptic
curve calculation itself takes negligible time even on my little
samsung netbook under Linux-Ubuntu(a little slower -as usual-
under windows7).
6.4 Download Links
My apologies, this is an amateur one
man show yet. So you find only binaries for the standard PC (i386
instruction set), for Linux(32bit and 64bit) and Windows (XP and
7) here. Mac users should be able to run the Windows version under
Wine. I regret not to be able to support different platforms with
binaries at this point. For everyone else I included the source code. You
need to have wxWidgets and GTK2.0 installed in order to build
Academic Signature.
(I did waste some hours though trying to get apple allow! me to
download the free compiler GCC on a borrowed mac-notebook to
produce an apple binary..... sorry guys - apple seems so
commercialized that I lost any interest in dealing with it,
-> use the wine windows emulator or compile the source
yourself.)
Please use the aca_sig download page(
in
german / in
english) for getting the latest version of academic
signature.
At the download page you will find
the latest versions of Academic Signature, my GnuPG signature of
the respective downloads, elliptic curve signature and timestamp
(incl. Makefile for Linux environment and code::blocks project
file). I publish this code under the GNU public license.
Find my public keys here: https://www.fh-wedel.de/%7Ean/crypto/academic_signature_key.html
If you use Academic Signature and especially if you download and
possibly alter the source, I would be happy to hear from you via an@fh-wedel.de.
6.5 Warmup with the Program
As a second warmup exercise you could convince yourself what happens
if a single bit is flipped after signing a document.
Sign a large wordprocessor document. Open the newly created *.ecsg
file for inspection with an editor of your choice. You will find the
domain name, the signature parameters "s" and "r" and an identifier
of the hash algorithm used for signature creation(e.g. Fleas_1_8,
SHA2, Fleas_lx , ... ). Inspect the signature file and close it
unchanged.
Verify the signature. Now open the signed document again and flip
one bit by changing one capital letter somewhere in the document to
lowercase. Close and save the marginally changed document. Convince
yourself that the signature is rejected now. This is by no means a
proof of the cryptographic security of the signing process but gives
you a basic idea of what happens in a blunt, unsophisticated fraud
attempt.
-> back
to content list
7 Usage
7.1 Proving
After the program is properly hatched on your systen (see section
6.2), you can prove the correctness of a signature. Open Academic
Signature and log in properly.
Select from the Menu "Elliptics->ellip_operations->ellip_Verify".
The
verification/proving Dialog opens. First you should locate the
signed document on your computer and select it via the button "select File to prove".
The signature file is supposed to be located in the same directory,
having the same filename as the document plus the extension ".ecsg".
Academic Signature suggests this signature filename automatically in
the editable line below the file name field. In case someone used a
different filename for the signature to add some personal flavour
(don't!), you can edit the filename/path of the signature file to
coerce it into something different.
Then select the public key that belongs to the person who signed the
document. Convince yourself that you can trust the source of the key
and that it indeed belongs to the person you presume and that this
person is indeed in the position to sign such document. Attention, this is indeed the most critical
part and achilles heel of ALL public key Cryptosystems!!!!
In some descritptions of usage of
digital signatures(e.g. in the german wikipedia entry about "Elektronische
Signatur" treating the
jurisdictional framework) it is stated that usually the signers
public key ist transmitted along with the signature for
convenience.......
Holy Cow!!!! I desperately hope these
statements are wrong and software vendors are in their right mind
and don't implement it like that. Checking a signature against an
attached public key has no
significance whatsoever! (The forger can always attach the filthy
key he has forged the signature with and claim it to be the
presumed signer's. Hopefully the writer of the wikipedia article
implicitly assumed, that the public key is tranmitted along with a
signature of the key issued by a trust center - it should be
called a "certificate" instead of a "public key" then.)
(I do admit that I am a sinner myself -Holy Cow!!! But checking the
signature of "Academic Signature" against my included public key is to mainly serve
as an exercise. Of course proper validation must be performed
against an independently retrieved version of my key from a
source of thoroughly evaluated trustworthyness.)
The very act of retrieving the public key from a trusted source
independent of document and signature file is an absolute core responsibility of the
prover.
....... Do you let salespeople pick the money for your
purchase from your wallet themselves for your convenience.....and
meanwhile look somewhere else....???
You can set the public key by three different methods:
a) Copy and paste Ax and Ay and the name of the
domain from some electronic document you trust. You may select and
type a key id and the signers name in the corresponding fields. This
is useful in case you store the key for repeated use. Key id is for
the program as a unique reference, Name of the holder is for your
personal reference(and can have twins with equal signer name). Hit
the blue "Prove ECCS signature" key and wait for the program to
proceed.
b) Import a public-key-file.
There are human readable public key files in a format understandable
for Academic Signature. It uses the extension "*.pell" for Public ELLiptic key and I suggest you
do the same. In the dialog for creating private keys there is a
button named "Export Public Part". Guess what it does... you'll find
a new *.pell file in your working directory. To use such a file in
signature verification, just hit the button "Import Pubkey from
file", select the file and use it. Of course you made sure you got
it from a trusted source. I recommend to store the public key
tamperproof for future reference in the protected internal store of
Academic Signature.
c) Retrieve a securely stored
public key from Academic Signature.
The button name is "Get Stored Pubkey". Select the one you want the
usual way (doubleclick or hit ok). That's it.
A file of 1 MB (more than enough for a letter of reference...) size
should roughly need 1 second for producing the unique hash-value.
The time scales linearly with filesize. The elliptic curve
calculations themselves take about twice the time as for signing and
need less than the blink of an eye for 256-bit domains on a new PC.
The result is displayed in the corresponding dialog field.
7.2 Presenting
The presenter has to transport the document(testimonial, letter of
recommendation, etc..) and the corresponding *.ecsg signature file
to the person who might be interested (if considered favourable by
the presenter) and hint to the presence of the digital signature.
Usually this will be simply done by e-mail. He/she does not even
need to touch the software "Academic Signature".
7.3 Signing
The process of signing needs some preparation i.e. key creation,
protected private key storing and public key publication. This has
to be done only once and should generally be stable for years of
use. If both steps have been done properly, the act of signing is
simple and moreless self explanatory:
a) Close your office doors and see that you are alone.
b) Create or reevaluate the document to be signed. Add/check for
correct place and date and the reference to your public key
publishing site. Put document into a special folder on your computer
that you find appropriate.
c) If others have been involved in the process of document creation,
make some invisible change(e.g. add a blank at the end of a
paragraph). This serves to harden against "Birthday
Attacks" towards the Hash.
d) Start Academic Signature and log in. Subsequently select "Elliptics->ellip_operations->ellip_Sign":
The
sign-dialog opens.
e) Click on the button "Select File"
and select the file.
f) The presently displayed key may be a dummy key, so select the
proper private key you intend to use from safe storage by clicking
on the Button "Select other Key".
After some consistency checks and a selftest(about 2 seconds on my
netbook), the selected key id and name is displayed in the dialog
fields.
g) Click on the button "Create
Signature". Academic Signature will put a *.ecsg file with
the document name as prefix into the same directory as the document.
Hashing will take about 5-10 seconds per Megabyte of document
length. The ECC operation takes about a second.
h) In the new version (from a09 on) you can choose the officially
approved hash-algorithm sha2 istead of the flea-hash Fleas_1_8.
(This is intended for the chicken among the users who don't dare to
use a new algorithm which admittedly the average crypto-guru
disapproves of. From version 10
on you may also use my improved, newly included version
"Fleas_3".)
i) Give document and signature file to the messenger (e.g. via
encrypted mail or memory stick) and be prepared to produce a
conventional, conventionally signed paper version as well.
7.3.1 Key Production
In elliptic curve cryptosystems this is the simplest possible thing
to do. Just select a random number of appropriate size, just a
little smaller than the group order "q" of the elliptic domain. (The
two other well established but less advanced public key
cryptosystems RSA and elGamal require somewhat more elaborate
private key selection procedures.)
In Academic Signature select the menu entry "Elliptics -> ellip_keys ->
Create/Load/Save_priv". The private-key management dialog
opens containing a dummy entry first.
a) Type the Key_ID you want the program to use as unique
reference(this one and all the following test lines are to be filled
without blanks each as a single connected string).
b) Type your full name into the field "Full Name"
c) Click on "Make New Key".
The fleas random generator will generate a random number of
appropriate size for you. This random number is your private key and
your elliptic curve signature secret for the next decades(if you
decide to use this one). Keep it secret and protect it with the same
alertness you protect your (eye)balls with ;-)
As it is just a plain old random number with no special properties,
you might type in any hex-number of sufficient length yourself. If
it happens to be too long, don't worry, Academic Signature will
moduloreduce it(modulus domain group order "q") to the right length.
Modreduction and recalculation of the corresponding public key (Ax
and Ay) will be triggered by hitting "Refresh_A".
If you don't fully trust my "weirdo-fleas" random generator(you have
to trust it for the generation of the ephemeral keys
though) or just want to add some personal flavor, you may
change a hex-digit here and there. Maybe you don't like nines
- so exchange a couple of them against f or a,.... this
number is all yours. If you happen to load my "my_trivial" stored
key for inspection you'll see that Academic Signature won't keep you
from selecting a stupidly insecure short key. If you like such a key
-so be it... (don't use such a key for serious matter though!).
d) If you like the key (it may definitely last longer than your car
or this implementation of Academic Signature, maybe even longer than
your marriage... - technically it is safe for decades) then deposit
it in the protected storage of Academic Signature by clicking on "Store". If you will have to
switch to a new computer environment in the future, you can take the
key with you. Just open Academic Signature for a last time, load the
stored key for inspection and copy and paste it to the future
location of your choice. (If you
happen to switch to a commercial implementation in the future,
chances are, the vendor will reject to accept your established key
and charge you a two digit $-amount for each NULL-effort to create
a new one.)
Your private/public key pair is bound to the domain, it is by no
means tied to this piece of software and can be used on any future
ECC-Implementation using the same domain. Mathematics -after all- is
the same in this Universe and others... The public part will not
change. The domain p256r1 used in Academic Signature is one of a
little more than 10 suggested domains on the ECC-Brainpool website
and is posted there for about ten years by now.
e) If you want to post the corresponding public key(Ax, Ay), you may
opt to export the public part - click on "Export Public Part" and Academic Signature will
create a corresponding *.pell file in your working directory.
7.3.2 Key Publication
In order to allow verification of your digital signatures, the
prover must gain trustworthy access to your public key. The method
of choice in the model of a mosaic of trust is to post it on your
university/corporate-website.
In addition to the public key, you should post contact data like
e-mail or phone to allow immediate clarification, if a signature
verification fails and gives rise to questions on the prover side. I
personally consider a picture of the signer(you) psychologically
helpful to lower the threshold for calling (in case your picture can
serve such purpose ;-)
The information must be embedded in a trustworthy corporate or
university web-environment. Only then can a prover assess of the
trustworthyness of the public key information and your competence
for signing such documents. You can find my key publication site here.
7.3.3 Key Lifetime
If you use the private key for -say- signing less than 100 documents
per year, the lifetime of the key can be decades and is only limited
by technical progress in computer power.
Certificates(which are basically just public private key pairs)
handed out by trust centers which are part of a PKI usually have a
limited lifetime. Please inspect some certificates deposited in your
internet browser (e.g. edit-> preferences-> advanced->
encryption-> View Certificates in Firefox). Interestingly I found
only certificates using RSA, mostly 2048 bit keys. They usually
expire within some years, in some cases in decades. 2048 bit
RSA-Keys are substantially weaker than the 256 bit ECC Key used by
Academic signature. So if they claim to be valid(under heavy daily
usage) till say 2035, you can sit back, relax and use your ECC-Key
safely till I'll be a hundred years old.
Of course, if compromised, the key has to be retracted immediately.
7.4 Institutional use
The present implementation is not adapted for institutional use for
say electronically signing all students graduation documents of a
university. On the other hand this would be a goal worth striving
for. Students would no longer need notarized copies of their
graduation documents for job applications.
This kind of use would need hightened security precautions and, to
some (purposely) limited extent, added usability tools.
a) A dedicated notebook for just this purpose of signing should be
prepared and stored in a safe and tamperproof place(e.g. a safe).
b) A website protected with high security level should be used as
public key presenter.
c) The person who is physically signing the fancy paper based
documents needs to create a personalized electronic signing key
bound to that person, keep it secret and guard that key properly and
professionally. This person and his/her assistants, who are usually
not acquainted with cryptography, should get a high quality briefing
on the do's and dont's of electronic signatures and the usage of
Academic Signature.
d) In order to fit into the current paperbased procedures, a
taylormade version of academic signature should be prepared, that
exactly mimics the classical procedures in place at the institution
at hand.(i.e. accept a file of Documents, eventually prepared and
electronically "pre-signed" as document list by an assistant etc.)
e) The act of signing should explicitly not be automated and remain a manual act of
conciously signing the personalized document by willfully clicking
on a button, while name of the graduate and grades are visible to
the signer next to the "sign"-button. The signed testimonial should
be manually given to the graduate e.g. stored on a memory stick
along with the fancy paper document.
The extra effort on the side of program developer(?s) would
certainly not be possible without adequate reimbursement and would
require an adequate time for developing and implementing the
additional features.
-> back to content list
8 Incentives for honest
Usage
8.1 Signer Advantage
Why should the signer go through the effort of understanding,
installing and using Academic Signature?
The advantage is that it serves the graduates. Doing them a favour,
making it easier for them to apply for jobs or school admissions is
a high value in itself.
Additionally digital signatures will be used frequently in the
future. So why not getting acquainted with the procedure now. It is
nice to already be experienced when we will begin using them for
everyday purchases, hotel reservations flight bookings or other
matters of daily life.
8.2 Messenger Advantage
Authenticated letters of recommendation can be distributed by e-mail
in a matter of minutes. No need to pay some authority to certify
that (paper) copies are authentic. Messengers need not care about
the number of copies any more, they can be infinitely aggrandized in
number. There is no second thought on the prover side about
authenticity because they are infinitely more difficult to forge
than a classical ink signature.
Additionally again the "first mover advanteage" in using digital
signatures in daily life applies.
8.3 Prover Advantage
The biggest advanteage is on the prover side. If considered
necessary, the prover can test the authenticity with great
confidence in the outcome in a matter of seconds. Even if he/she is
not very well acquainted with the signer. Try to seriously assess
the authenticity of an old fashioned ink-signature on a document
signed by a person you barely know..... it's impossible, at least
extremely cumbersome.
Additionally again the "first mover advanteage" in using digital
signatures in daily life applies.
->
back
to content list
9
Incentives for Attack
9.1 Discrediting Signer by Verifier
This is a minor incentive. As mentioned above rejection of modern
means of authentication, jealousy or the attempt to cover computer
illiteracy could be a driving force for e.g. falsely claiming
rejection of correct signatures. The signer can ameliorate a
potential incentive if he/she consequently also hands out classical
paper based versions. It might be in the messengers best interest
not to get a job with this potential employer of questionable
credibility(Professor Vain) anyway.
9.2 Obtaining false Testimonial or
Changing Testimonial
This paragraph deals with the strongest incentive for defecting and
fraud attempts. It is obviously of high value to a weak or morally
inappropriate applicant to obtain false testimonial.
Attacks from this side will happen.
These could include creating fake signer identities altogether,
creating a fake website presenting a key which the messenger created
hinself or presenting a document that was signed before the
messenger was caught doing something morally inappropriate. The
incentive for attack is very high but the power of an attack would
be limited though. The resources of a single individual especially
in the presence of intellectual weaknesses are to be taken seriously
but are not too fearsome.
The most likely attack under these circumstances appears to be the
empty office ambush to get hold of the private key, if the signer
does not apply due diligence in the use of Academic Signature.
Another attack might involve the use of a compromised key where the
holder of the key did not properly react to or did not get knowledge
of the public exposure of the key. If Academic Signature gets
widespread acceptance, the availability of such compromised keys on
the web must be expected. The long term neglecting behaviour of a
previous signer should be considered immoral. Future behaviour of
provers should include checking for blacklisted keys and seeking
contact with the holders of suspicious keys.
9.3 Discrediting Messenger by
Verifier
This incentive is related to incentive 9.1. The messenger may
ameliorate the incentives by consistently falling back to classical
paperbased documents if he/she picks up the slightest hints about a
possible computer illiteracy of the verifier. Again, it might be in
the messengers best interest not to get a job with this potential
employer of questionable credibility anyway.
9.4 Discrediting Messenger by
Signer
Again the incentive is minor. Nevertheless out of emotional reasons
a signer might feel inclined to discredit the messenger by giving
out false unverifiable signatures. The best protection for the
messenger ist an independent check of the correctness of the
signature on his/her side.
9.5 Signer repudiation
If the signer gets to know disqualifying facts about the messenger
after the testimonial was signed, this should not have any influence
on documents containing prior judgements. Nevertheless, a signer
might condemnably try to repudiate the signature by deleting or
changing the published key especially if there have been very few
signatures created with this key. There is no real protection for
the messenger against this behaviour. If the messenger suspects such
repudiation, he/she should consistently fall back to using the
classical paper version.
->
back
to content list
10 Most
Promising Modes of Attack
10.1 Hacking/Substituting Public
Key Presenter Webpage
This is the most likely mode of
attack for Dr. Mallory trying to improve her chances to get
a desired position, she would not get otherwise.
This is a blunt and fairly unsophisticated attack.
Dr Mallory has limited intellectual capbilities and/or was cought
employing fishy moral standards. Still she is able to copy Professor
Smarts website, modify it(e.g. change the posted public key against
a new creation owned by Dr Mallory) and post it at another location
in the www.
This is fairly easy to do even with limited computer literacy. Then
Dr Mallory could write her own testimonial, sign it with her newly
created private key and send testimonial and signature to Professor
Veryrich along with the false claim that it was signed by Professor
Smart and the hint to verify the signature at the fake website.
In order to prevent such
attack, Professor Veryrich has to make sure the key presenting
website is embedded in a professional corporate or university
website, which is his main duty anyways. This will easily expose
such fraud attempt.
A rather sophisticated variant
involves hacking the presenting website and only exchanging the
presented key against a fake key. This leaves the website embedding
intact and is hard to detect by Professor Smart(who may not know his
public key by heart) and impossible to detect by Professor Veryrich.
This exchange may go unnoticed up to the next verification attempt
using a true signature, which will subsequently fail and expose the
attack.
In an even more sophisticated version Dr Mallory will try to guess
the time interval of Professor Veryrich's proof of the signature
(which is hard!) and return the public key to the correct version
after proving presumably took place. Under these circumstances the
fraud may even go unnoticed. The timing of this attack is critical
and risky and it requires high expertise.
Hopefully some Dr Mallory featuring the talents neccesary for
successfully applying this variant may not need a fake testimonial
and may get a well payed job with a data-security company or a
national secret service anyways.
Morale from this second variant:
A) Strongly protect the
key-presenting website.
B) You should check the
validity of the key presented in your name on a regular basis.
This may be done easiest by learning a specific short excerpt of
the public key by heart and having a look at the website -say-
once a week.(Hard for a new key, easy after an extended period of
using the key.)
10.2 Substituting/Manipulating
Signer Software
Dr Mallory might replace Professor Smart's copy of "Academic
Signature" by a copy which will leak login key, private key info or
other information to her computer and thereby breach security.
Depending on the degree of sophistication this may result in
A) creation of dysfunctional signatures that can't be proven.
->This would be a minor problem and will be easily detected.
B) Leaking your login-key to Dr. Mallory. This requires a medium
level of sophsitication. Knowing your login key might enable Dr.
Mallory to sneak into your office, start your computer, start
Academic Signature and read out your private key and use it for
creating signatures with undetectable fakeness. As you see, there
are several additional barriers to breach. Your office must be
unlocked and unattended, Dr Mallory must have the capability to log
into your computer and -if this barrier is also in place- must also
be able to mount your independently protected veracrypt drive.
This is very difficult if you are applying due diligence in using
academic signature. However it may go undetected and leave a lot of
time to break the additional barriers that remain after the login
key has been compromised.
If Professor Smart is suspicious, he may verify my signature for the
program. Catching and redirecting this task would required a
sustantially heightened level of sophistication(and knowledge of the
original C++-code) on the attackers side.
C) At the highest level of sophistication, thorough knowlege
of the program code could allow Dr Mallory to introduce a
spy-addition to the program that detects the brief moment in time
during signing, when the privat key is present in plaintext. The spy
addition could then directly transmit key information to Dr.
Mallory. Again the presence of an altered program would be
detectable by proving my signature of the program. A Dr. Mallory of
that level of sophistication could, however, be capable of catching
and redirecting this verification request also. A super paranoiac
Professor Suspicious-Smart could still have the means to detect the
alteration if he secretly signs the copy of Academic Signature with
his first key shorly after hatching. He then hides this signature at
some remote place on the countryside of his harddisk and check for
the correctness of this signature every time on starting Academic
Signature.
But let's not get carried away here again. Professor Smart's
opponent -after all- is neither Microsoft or the KGB nor the NSA but
a mediocre graduate trying to fake a letter of reference.
I consider attacks of this type unlikely - they are very difficult.
Morale:
A) If you use windows, at least
protect it by a login keyword.
B) If you are a little
paranoid, frequently check the validity of my signature of the
program.
C) If you are a full blown
paranoiac, quickly sign the program after hatching with a
dedicated key, hide and encrypt this signature and regularly test
the validity of this secret signature.
D) Non-paranoiacs may just sit
back and relax - I consider this type of attack unlikely.
10.3 Substituting/Manipulating
Prover Software
This attack is related to 10.1 "substituting key presenter webpage"
and may develop into 10.2. Dr Mallory, upon presenting her
digitally signed letter of reference, hints to a forged website for
downloading a compromised version of academic signature to the
prover. If Professor Veryrich has little computer literacy, Dr
Mallory can have reasonable chances of success.
The attack is much harder to mount than 10.1 since Dr Mallory has to
produce a trustworthy looking faulty variant of academic signature.
The damage can be much higher though, since Professor Veryrich may
continue to use this compromised version and may even begin to sign
documents himself with this "trojan" program. Luckily he probably is
educated enough to know about the risks of downloading software from
the net and running it. So we can expect that Professor Veryrich
takes due care to assess the trustworthiness of the download site
with established "reflexes" and is naturally more suspicious in this
step than in acquiring Prof Smarts key. I consider this type of
attack as far less likely than 10.1 (Hijacking the key-presenter
page) but more likely than 10.2 (manipulating signer software
directly).
Morale:
After downloading Academic
Signature from a webpage of thoroughly asessed trustworthyness a
cautious will-be-prover should first verify the integrity of
Academic Signature using my key not from the accompanying key
repository but using my public key taken directly from my key-presenter webpage.
10.4 Stealing Private Key / Coffee
Break Office Ambush
The naive Signer, Professor Simplemind may be logged into Academic
Signature and be about to sign a testimonial. Dr Mallory, an
attractive woman in a miniskirt and highheels offers a nice fresh
cup of cappucino and has an urgent question about some favorite
topic of Professor Simplemind's research. Professor Simplemind -like
being hypnotized- leaves his computer and his office to the coffee
room to discuss his favourite topic with Miss Mallory immediately.
In the meantime Oscar, DrMallory's wannabe lover sneaks into the
office, gets into the "load private key" dialog, takes a snapshot of
Professor Simpleminds private key, restores the initial windows,
leaves the office with his prey and is happily expecting
acknowledgements of Dr Mallory's gratitude.
This of course results in a catastrophic security breach and
severely damages Professor Simpleminds reputation if Dr Mallory is
eventually caught later on using fake recommendations from Professor
Simplemind.
This archaic mode of attack is with us since the dawn of mankind -
even longer - chimpanzees are good at it too - not in ahuman society
though ;-)
Come to think of it - a chimpanzee lady in red miniskirt with
highheels, shaved legs..in the coffe kitchen...... This might
attract enough attention to seduce Professor Simplemind to drop his
shields and leave Academic Signature unattended.
Again - let's not get carried away here, this is a serious manual
and I should stop molesting you with my sick sense of humor. To my
knowledge the KGB doesn't hire chimpanzee-secret-agents anyways.
Morale:
The signer must avoid leaving
Academic Signature in a logged in state unattended and rank this
as comparable to leaving his wallet open and unattended on a bench
at a trainstation.
10.5 Concurrently Running Malware
If your computer is infected with dedicated spy malware which runs
in parallel with academic signature, there is no security and no
secrecy - Professor Smart has no chance and is lost.
This is the main reason for using key bearing smart cards and
separate card readers for electronically signing e.g. with the new
german id-card.
(This introduces new possibilities for attack, however -e.g. what
file are you really signing? In my opinion, if your computer is
infected with dedicated malware, you are still lost even if your
private key stays protected on the smart card. It is just a dump of
responsibility on you(the end user). Using the private key, securely
sitting in the smart card, is still at the malware's disposition, so
don't be surprised if you get a delivery of 537 overly expensive
electric blankets along with 213 magazine subscriptions which you
supposedly ordered last month.....)
Morale:
A) Use Linux.
B) If you must use windows,
make sure that you always have a firewall and an up to date virus
scanner on duty. (I recently heard rumors that in addition to
microsoft, the NSA also has a key to "update" your windows-system
:-))
C) You may increase security somewhat if you keep internet
browsing with the signing computer to a minimum and always do it
with all the well known security shields up(no java, no java
script, no Adobe flash player, use a different non-administrator
user identity for browsing, hide browser info and id, surf
anonymously, etc..etc..etc....)
D) Never install software from
an untrusted source (except
"Academic Signature"....... I know, I know ...... read this
manual and decide if you can trust me... this is officially
called a "semantic test"
and should also be element of the mosaic of trust as recommended
in chapter 1 for acceptance of e-signed testimonials).
10.6 Hardware Theft&Analysis
Dr Mallory may wait for Professor Smarts department to have chrismas
celebration at some remote restaurant. While he and his colleagues
are having fun eating roasted suckling pig, Dr Mallory may get into
Professor Smarts office with a duplicate (old fashioned metal)key,
steal the computer or exchange the harddisk with a new one
containing a copy of the original contents. In case of a hidden disk
exchange, she may even lock Professor Smarts door again to keep the
intrusion secret.
She then brings her prey into the fleabag-filthy hacker appartment
of Oscar to get the disk analyzed. In case Professor Smart did not use a separately encrypted
domain for Academic Signature and the "/secrets" folder, Oscar will
find fragments of or even a full version of your secret key in the
"deleted" parts of your harddisk. Dr Mallory can then write her own
testimonials and sign them with Professor Smarts key unnoticed - a
catastrophic security breach.
This attack is efficient and does not need high sophistication on
the attackers side, it is thus likely.
Morale:
Academic Signature should
reside on an independently/additionally enciphered domain on your
harddisk (as recommended). Use e.g. veracrypt or the ubuntu-option
to encrypt your home directory. (The second option is weaker against other attacks
like the coffee break office ambush since you tend to remain
locked into the system permanently during working hours, whereas
when using, you -hopefully- only mount the protected domain as
long as you need it.)
From version 14 on, this threat is
counteracted by introducing a second layer of encryption for
private keys, that will only be lifted in memory for a brief
moment. Private keys are never ever present in plain on harddisk
any more. A relocation of memory to the swap exactly in the brief
moment of key exposure is always possible but unlikely. Thus using
academic signature version 14 or higher on a non encrypted drive
may now be tolerable.
10.7 Spy Cameras or Rubber Hose
Cryptoanalysis
A) Dr Mallory may fix a hidden camera in your office or pick um
EM-stray radiation emitted by your monitor in the room next door to
reconstruct your screen image and get hold of your login key or even
your private key. Academic Signature purposely does not always hide
secret letters on screen with fat bullets. (This is avoided for now to promote
tranparency for the user in the introductory phase and may be
introduced again in future versions.)
B) Dr Mallory may send Oscar, the six foot tall former "nose guard"
of the local football team to "convince" you that Dr Mallory
deserves good testimonial. She may threaten to send you the ears of
your abducted pet or make a barbecue with your kids guinee pigs -
use your fantasy - this is called "rubberhose cryptoanalysis". It is
cheap, easy and effective. Nowadays kids seem to learn this in
elementary school already.
C) Special options arise for Dr.Mallory in a country under a
dictatorship. She may be close to THE PARTY and threaten to grass on
you and tell them you listen to the wrong radio stations with all
"due" consequences. Please note that this was a real threat even in
part of my country only about little more than twenty years ago! A
PKI(Public Key Infrastructure) and use of asymmetric encryption is
useless if you are a citizen of -say- iran, china, syria,..... (or a
"citizen" of guantanamo for that matter). Under a totalitarian
regime you'd need steganography
and the like - but that is stuff for secret agents, spies and
revolutionaries, certainly not my prime field of interest.
Morale:
For a public key infrastructure to work, you need a
political system that respects basic human rights and individual
freedom. Additionally you need an IT-infrastrucutre that is not
dependent on a monopolist software vendor(now who may that one be?) and not on a monopolist search
engine supplier (and
who the hell may this one be??). If that is not the case, there is no
security and there is no privacy.
10.8 Breaking Academic Signature
If I introduced errors in the implementation of ECDSA, Dr Mallory
may exploit them.
There is a well encapsuled long number arithmetics module which I
spent a lot of time testing and optimizing. It served well in former
applications of RSA and elGamal and now I use it for elliptic curve
calculations. I wrote it entirely myself and know there are e.g. no
"rare long carry chain errors" (they can easily be detected working
with smaller numbers) and no "machine-specific" optimisations. (You
learn nice facts seemingly unknown to some cryptography authors if
you delve into this - I learned e.g. that long number division and
modreduction is surprisingly fastest if doing it bitwise even in
high level language and not employ the 4 byte "div" command of the
processor ;-).
If you take someone elses long integer module(as e.g. one of the
most famous security gurus and my most appreciated book author Bruce
Schneir recommends), you never know what's really in it and must be
extremely cautious and spend a lot of additional time for testing.
Believe me, if it is entirely yours, you know what you are dealing
with and feel much better. So I consider it extremely unlikely that
my integer arithmetics contains errors which could eventually be
exploited. (How could that be anyways? Did such an attack ever occur
? Or is it just a line of security advisors to scare the sh.. out of
developers...)
There is -of couse- a module containing the elliptic curve
operations (point addition, point doubling, point multiplication).
However, these are fairly transparent and not very complicated. Some
limited complexity is added, if you introduce projective
coordinates. Still this is all rather transparent and -to my deep
belief- error free in Academic Signature. (The core routines were
coded within one afternoon and did work correctly on first
compilation, a projective coordinate version of point
multiplication(about tenfold speed!) was extensively tested against
the plain version.) So again, I would not try to attack this
implementation, I believe the implementation is correct. Mathematics
after all is a much more orderly, regular and transparent topic to
be coded than the dirty day-to-day business e.g. creating GUIs using
error prone tools.
Morale:
Relax! I am quite confident
about this aspect.
10.9 Breaking the ECC-Algorithm
Forget it. For more than a
decade bright people have tried to find a way and did not find it.
Each slight partial success has been countered by improvements in
domain parameter selection. The Elliptic Curve Cryptosystem is
considered to be the most "futureproof", safest and most advanced
asymmetric cryptosystem.
Morale:
Don't worry about this one
unless the "quantum computer" is fully operational and we all
think in q-bits.
10.10 Breaking Dancing Fleas Hash
This may be possible.
Academic Signature uses my newly created hash algorithms of the
"fleas" family. They adhere to the "Merkle-Damgard Construction". I
use them with up to 2048 bit length(They are freely scalable but
more efficient with powers of two bytelength (-> 128 byte). They
are slow compared to e.g. sha2 which you may use alternatively(for
chicken ;-). I favoured (my gut feeling of) security over speed of
execution.
A) The long bitlength gives good protection against brute force
attacks.
B) It yields good random properties of the hash value(and the
intermediates!) - checked with the "Chi^2 goodness
of fit test".
C) The "extension
problem" is solved by applying the primitive
"Fleas-block-randomization" three times with the last block(twice on
intermediate blocks).
(Sorry, the explanatory
link may be volatile, but I couldn't find a good reference in
wikipedia or other more permanent locations....)
D) The primitive "Fleas-block-randomization" contains two finishing
steps to "seam" the block-result against backwards unraveling
without decreasing apparent entropy. The last of these steps
consists of producing two independent, apparently random looking
block-derivatives. These are finally xored to yield the resulting
block and thus seam the exit. I believe that the combination of
establishing even statistical distribution and a safe blocker of
backwards unraveling is safe. I furthermore believe my xor-blocker
is related to a one-time-pad and is safe.....
Morale:
Please attack the hash (the
code is available in the archive aca_sig_bxx_sout here) and tell me
about the results. I myself am confident and prefer it over sha2.
10.12 Manipulating/Breaking the
Random Number Generator
A weak RNG is a prime target for attack. I believe the "Fleas RNG"
is strong and no promising target. Again I prefered (my gut feeling
of) safety over execution time. Version 10 features an improvement of (my gut feeling of)
RNG security over version 9 by using two different versions of
state-vector propagating one-way-functions. I combined them to
create a fully protected internal state propagated by
(presumed)one-way function "a" and a random byte pool derived from
the current internal state by (presumed)one-way function "b". The
derivation of the byte pool from the internal state via "b"
triggering a propagation of internal state vector via "a" for the
next round.
A) The RNG state vector is initialized with an "ephemeral" file,
e.g. a picture just shot with your webcam, that should be deleted
afterwards. So the initialisation is seamed.
B) It relies on the "Fleas" randomizing function partially described
in 10.11.
C) The length of its internal state is a formidable 2011 byte(this
year! of course it is scalable).
D) During program execution, the secret internal state vector is
occasionally re-randomized with the current timer readout as
external input.
E) Each third byte is read
out and used as random number, two thirds of the state remain
secret in version 9. From version 10 on, the internal state
vector is fully protected by generating the random pool via a
(presumed) one-way function from the independently propagated secret
internal state vector. If the 2011-byte random pool is used up, the
secret internal state vector is propagated and a new pool is derived
via a one-way function again.
Statistically after 2(state-vector bitlength/2)
propagations of a perfect PRNG a reentrant number is to be found.
This causes a severe entropy collapse in subsequent output - so
after at most 1/10 of this usage-number(never reaches this age in
practice), the secret internal state is re-randomized with an
external input. (The
routine is internally called "sexwith(state long integer, external
long integer)" in analogy with sexual mixing of the gene pool in
diploid life and resets the RNG-age parameter).
F) The internal state is stored with cryptographic protection to be
deciphered, re-randomized and reused during the next session of
Academic Signature.
Hey, go and attack it and then communicate with me about the result.
Morale:
Yes, it may be attacked. This
could be successful. But chances are the "Fleas-RNG" is safer than
what you have been using before. To my knowledge, there is no
officially recommended standard for chicken users yet(There are
suggestions around how to test RNGs though which -frankly- mostly
seem very simple). Thus you are stuck with it. I wouldn't worry
too much about this.
->
back
to content list
A Version of
section 11 is available in pdf-Format here. It is digitally signed
by the author. Find signature file here.
11.1 License
Note: On Feb
6, 2012 I published the source code and changed the license
explicitly to the GNU public license.
As stated earlier, the project
academic signature is my personal one man show (yet) and my time
resources are limited. Most work had been done in my spare time
and in this summer vacation. Thus I do not want to waste time on
dealing with legal matters. Dealing with legal matters at all
(even in the case of public licenses) cannot be taken lightly, so
I avoid it altogether and shall just describe my intentions in
plain lay language to the public.
My main interest lies in creating a
high quality, secure software solution, usable according to the
protocol described in previous sections, embedded in a
comprehensive security framework based on a thorough threat
analysis, part of which has also been presented in previous
chapters.
Since each single one of all the
marvelous tools(Linux, wxWidgets, wxSmith, code::blocks,....) used
to produce "Academic Signature" is open source, public license,
and all the theoretical background was given to me from the free
and open academic community, I feel obliged to make "Academic
Signature" available for everyone, everywhere at no cost.
11.2 Ownership
Since I am the author of each and
every line of soucecode (except a small subroutine for sha2), I
consider the sourcecode of "Academic Signature" being my
intellectual property.
In contrast with most software
vendors, however, I draw a clear line between this intellectual
property and ownership of the binary you downloaded from my
website.
I consider the binary as entirely
yours, it is your property, do with it what you want.
If you feel like it, you can delete
it without a trace. (Try this with the stupid MSoffice teaser or
its cronies you cannot avoid being dumped on you if you buy a new
windows PC; they tend to stick with you like lice or ticks.) Or
you may copy the "Academic Signature" binary 1000 times and send
it to all your friends around the world or post it on your
website. You may also reverse engineer it, if you like to do so.
(It might be easier, though, to just ask me for the code of a
specific module.....)
I consider it mandatory that security
relevant software and all its data -of course- has only one
master: You, the user which it was imprinted on during hatching of
the binary.
I clearly and purposely abandon
control over your copy and/or installation of "Academic
Signature".
11.3 Disclaimer
"Academic Signature" assumes a
heightened level of computer literacy among its users and it
furthermore gives itself the luxury to suppose that you read the
manual before using it.
Still, I am human, you are human and
"Academic Signature" is a program. So it may contain bugs, logical
inconsistencies, misleading labels on buttons, may become victim
of a trojan or virus attack or may be used inappropriately by you.
In all these cases I will not bear
any responsibility for resulting financial damage. You use the
program at your own risk.
I would morally feel responsible to
some degree though and promise to continuously fix bugs brought to
my attention. I furthermore promise to continuously fortify
possible targets for attacks in upcoming updates.
-> back to content list
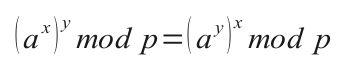 Onewayedness
and commutativity of the function application are sufficient to
perform a so called Diffie-Hellman
Key exchange and the so called elGamal encryption.
Onewayedness
and commutativity of the function application are sufficient to
perform a so called Diffie-Hellman
Key exchange and the so called elGamal encryption.