Beim Selection Sort wird zum Beispiel das kleinste Element gesucht und am Anfang der Datenstruktur (z.B. einem Array) angefügt. Danach wird der Feldrest entsprechend weiter durchsucht und wieder das nun kleinste Element am Ende des Feldrestes angefügt. Entsprechend wird das immer kleiner werdende Restfeld bearbeitet. Dabei werden die die Plätze der gewählten Elemente vertauscht. Mit dem oben genannten Beispiel würde es wie folgt aussehen:
gebaeudereiniger = a wird mit g getauscht
aebgeudereiniger = b wird mit e getauscht
abegeudereiniger = d wird mit e getauscht
abdgeueereiniger
Der Vorteil von Selection Sort gegenüber Bubblesort liegt in der Art, wie ein Element an seinen Zielort transportiert wird: Bei Bubble Sort wird ein Element an seinem Quellort herausgenommen, alle Elemente zwischen dem Quellort und dem Zielort um eine Position verschoben und dann das Elemente an seinem Zielort eingefügt. Selection Sort vertauscht nur die beiden Elemente am Quell- und Zielort und läßt alle Elemente dazwischen stehen.
Zur Verdeutlichung hier nochmal ein Beispiel mit Zahlen
4 9 3 2 5
2 9 3 4 5
2 3 9 4 5
2 3 4 9 5
2 3 4 5 9
Eine Analyse der Durchgänge von Selection Sort:
Worst case und Average case:
Zwei ineinander geschachtelte for-Schleifen
n - 1 + n - 2 + n - 3 +...+ 1
= ![]() i =
i = 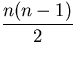 =
= ![]() -
- ![]() = O(n 2)
= O(n 2)
Das folgende Struktogramm zeigt den Algorithmus schematisch:

Quellcode Selection Sort in Pascal :
procedure selection_sort (anz: integer; var a: feld); var i, j, k, x : integer; begin for i := 1 to anz - 1 do begin k := i; x := a[i]; for j := i + 1 to anz do if a[j] < x then begin k := j; x := a[j]; end a[k] := a[i]; a[i] := x; end; end;Quellcode Selection Sort in C :
void selection_sort (int anz, int a[])
{
int i, j, k, x;
for (i = 1; i <= anz; i++)
{
k = i;
x = a[i];
for (j = i + 1; j <= anz; j++)
{
if (a[j] < x)
{
k = j;
x = a[j];
}
}
a[k] = a[i];
a[i] = x;
}
}
Legende :
anz = Anzahl der Elemente a = ein Array i, j, k, x = Hilfsvariablen
Für einen durchschnittlichen Datensatz braucht Selection Sort etwa O(½n2) Vergleiche und O(n) Vertauschungen. Selection Sort ist gegenüber Bubble Sort im Vorteil, wenn das Vertauschen (d.h. Kopieren) von Elementen aufwendig ist.
Im oben genannten Beispiel "gebaeudereiniger" benötigt Selection Sort maximal 15 Durchläufe um die Datenstruktur zu sortieren. Da aber in der Regel einzelne Elemente bei den jeweiligen Durchläufen ihren Platz verbesser oder sogar ihre Endposition erlangen, ist die Datenstruktur in diesem Beispiel bereits nach 11 Durchgängen sortiert. Im Vergleich mit Bubble Sort kann man eigentlich sagen, daß sich qualitativ nicht viel tut. Im Gegensatz zum Bubble Sort bricht Selection Sort aber bei einer vorzeitigen Sortierung nicht ab, sofern Bubble Sort dahingehend optimiert wurde. (siehe dazu Bubble Sort)