Insertion Sort geht in gewissem Sinne den umgekehrten Weg von Selection Sort: Von vorne nach hinten im Datensatz wird ein Element nach dem anderen ausgewählt. Für ein ausgewähltes Element wird im vorderen, schon sortierten Teil des Datensatzes die passende Position gesucht. Dann wird an dieser Position durch Verschieben des restlichen Abschnittes Platz geschaffen und das ausgewählte Element eingefügt (daher der Name des Algorithmus). Diesen Algorithmus wenden die meisten Leute an, wenn man sie bittet einen gemischten Kartenstapel zu sortieren.
Beim Sortieren einer Folge von N Elementen durch Einfügen werden die Elemente nacheinander betrachtet und in die jeweils bereits sortierte (am Anfang leere) Teilfolge an der richtigen Stelle eingefügt. Das erste Element bildet bereits eine sortierte Teilfolge, ein Vertauschen ist nicht notwendig. Begonnen wird also mit dem zweiten Element der Folge. Ist es größer als das erste Element, bilden beide Elemente zusammen die korrekt sortierte Teilfolge; ist es kleiner als das erste Element, so muß es an die richtige Stelle verschoben werden. Das Verschieben erfolgt derart, dass das Element sukzessive mit dem jeweils nächsten, weiter unten stehenden Element der bereits sortierten Teilfolge verglichen und gegebenenfalls mit ihm vertauscht wird. Dann ist das dritte Element an der Reihe, um an die richtige Stelle verschoben zu werden. So wird nacheinander mit allen Elementen der Folge verfahren.
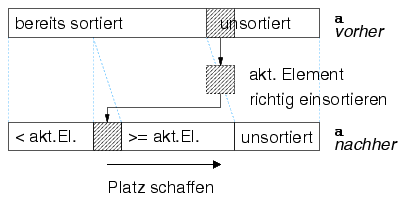
Anmerkung: Insertion Sort benötigt im Durchschnitt ungefähr 1/4 N^2 Vergleiche und 1/8 N^2 Austauschoperationen und im ungünstigsten Fall doppelt so viele.
Das folgende Struktogramm zeigt den Algorithmus schematisch:

Quellcode Insertion Sort in Pascal:
procedure insertion_sort (anz: integer; var a: feld); var i, j, k, x : integer; begin for i := 2 to anz - 1 do begin x := a[i]; a[0] := x; j := i - 1; while x < a[j] do begin a[j + 1] := a[j]; j := j - 1; end; a[j + 1] := x; end; end;Quellcode Insertion Sort in C :
void insertion_sort (int anz, int a[])
{
int i, j, k, x;
for (i = 2; i <= anz; i++)
{
x = a[i];
a[0] = x;
j = i - 1;
while (x < a[j])
{
a[j + 1] = a[j];
j--;
}
a[j + 1] = x;
}
}
Legende :
anz = Anzahl der Elemente a = ein Array i, j, k, x = Hilfsvariablen
Für einen durchschnittlichen Datensatz braucht Insertion Sort etwa O(n2/4) Vergleiche und O(n2/8) Vertauschungen. Gegenüber Selection Sort vergleicht Insertion Sort weniger, kopiert aber mehr(Diese Aussage gilt nur für einen hinreichend großen Datensatz). Man spart im Average Case einige Vergleiche, da beim Aufspüren der Lücke im Schnitt nur die Hälfte aller maximal Notwendigen Vergleiche durchgeführt werden müssen. Zum Vergleich: Selection Sort benötigt immer alle Vergleiche, um minPos zu finden. Im Gegensatz zum Selection Sort profitiert Insertion Sort von einem vorsortierten Array und kann dann schneller agieren.