zurück zur
Homepage zurück zur Kurshomepage Statistik
Monte Carlo Simulation zur Generierung der Student-t Verteilung mit
Maxima
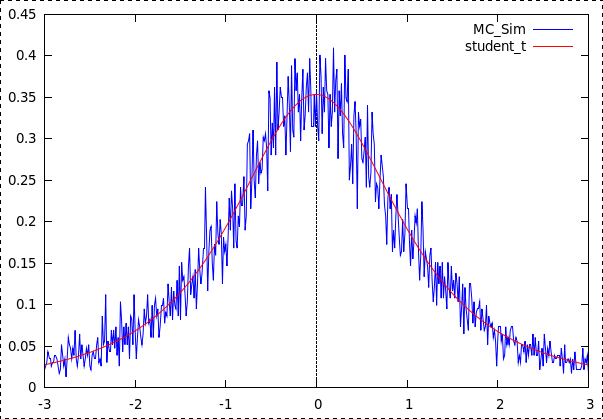
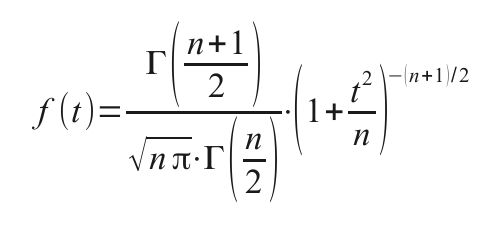
Die Herleitung der expliziten Formel für die Student-t Verteilung
ist schwierig, würde eine
normale Statistikvorlesung sprengen und wird deshalb in aller Regel
nicht präsentiert.
Man kann die Verteilung und deren Anwendung aber trotzdem verstehen,
wenn
man eine Monte Carlo Simulation versteht, die sie generiert.
Sie können das auf Ihrem Computer durchführen und der
Verfeinerung bei größer werdender "Schusszahl" der
Simulation zuschauen.
Sie brauchen dafür lediglich die kostenfreie und sowieso
überaus nützliche Software(Open Source/Public License) Maxima
für
symbolische (und auch numerische) Berechnungen:
1. Ich
empfehle wxMaxima, das Sie von hier
kostenfrei für alle Betriebssysteme herunterladen und dann
installieren können.
(Hinweis:
Linux-user finden das Paket in der Regel auch in Ihren Repositories.)
2.
Folgende kleine wxMaxima-Zelle "maxima_student_t.wxm" bekommen
Sie von mir. Laden Sie sie herunter und legen Sie sie an einem Ort
Ihrer
Wahl auf dem Computer ab. Mit dieser Zelle erzeugen Sie eine Monte
Carlo Simulation zur Student-t Verteilung zu 2 Freiheitsgraden.
(Hinweis:
Wegen
verschiedener
Zeichencodierung
in
verschiedenen
Umgebungen
können
die
Umlaute
in Ihrem Editor eventuell etwas wunderlich dargestellt
werden - das ist aber kein Problem, da das nur in Kommentarzeilen und
auch nur außerhalb von wxMaxima auftritt.)
3.
Öffnen Sie einfach die Zelle "maxima_student_t.wxm" mit
wxMaxima.
(Hinweis:
Sicherheitsbewusste Besucher können auch den unten
auf dieser Seite wiedergegeben
Inhalt selbst abtippen oder per Copy and Paste in eine leere
wxMaxima-Zelle
einfügen.)
Starten Sie die Berechnung der Maxima-Zelle(Gehen Sie mit dem Cursor in
das Programm
und drücken Sie "shift return").
Die Berechnung kann durch Schließen des Maxima-Haupt-Fensters
vorzeitig abgebrochen werden.
Hinweis:
Unter Windows (XP) werden die
Iterationsblöcke jeweils durch Schließen des Plotfensters
getriggert.
Unter Linux (Ubuntu Lucid) erfolgen die
Iterationsblöcke mit Grafikaktualisierung automatisch und werden
bei gleicher Hardware etwa in doppelter Geschwindigkeit ausgeführt.
Kleine Knobeleien zum Schluss gefällig ?
A: Welche (zwei !) Zahlen müssen geändert werden, um die
Verteilung für 3,4,5,..n Freiheitsgrade zu generieren ?
B: Wie könnte man die Maxima-Zelle abwandeln, um einen
größeren Wertebereich als -3 - +3 zu erfassen ?
C: Wie könnte man die Maxima-Zelle abwandeln(vereinfachen), um die
Standardnormalverteilung zu generieren ?
Der Inhalt der Maxima-Zelle ist
hier
wiedergegeben:
/* [ Created with wxMaxima version 0.8.4 ] */
/* Die Maxima-Pakete "distrib" und "descriptive" enthalten statistische Funktionen */
/* und werden für diese Simulation gebraucht */
load (distrib) $
load (descriptive);
/* Die Simulation benötigt normalverteilte Zufallszahlen */
/* Diese effizient aus rechteckverteilten Zahlen zu erzeugen ist nicht trivial */
/* Unter Maxima scheint das Verfahren nach Marsaglia am besten zu laufen*/
/* die jetzt definierte Funktion "gaussdm" erzeugt bei Aufruf eine standardnormalvt. Zufallszahl */
gaussdm():= block(s:2,for im:1 thru 900000 while s >= 1.0
do block(x:random(2.0)-1.0, y:random(2.0)-1.0, s:(x^2 +y^2)),ret:y*sqrt(-2.0*log(s)/s)/*,if x>y then ret:-ret ,ret*/);
/* Die Liste "t_carlo" wird in einer Länge von 480 Elementen erzeugt und zunächst mit Nullen gefüllt */
t_carlo:makelist(0.0,x,-240,240)$ /* Sie soll später die Treffer der MonteCarlo Simulation akkumulieren */
/* Die Liste "tru_t" wird in einer Länge von 480 Elementen erzeugt und */
/* mit der "richtigen" Student-t-verteilung aus der distrib-Package befüllt */
/* Die Liste gibt die Werte von -3 bis +3 wieder ->(240/80 = 3) */
tru_t:makelist(pdf_student_t(1/160+x/80,2),x,-240,240)$
/* Die Liste "xval" wird erzeugt. Sie trägt die äquidistanten x-Koordinaten von -3 bis +3, die für den Plot */
/* jeweils der echten Student-t und der MonteCarlo-Simulation zugeordnet werden */
xval:makelist(x/80,x,-240,240)$
/* Die Funktion normlist wird definiert, die Liste "lst" auf eine bestimmte "norm" normiert */
/* Wird für den Vergleich im Plot benötigt, schliesslich soll unabhängig von der Zahl der Schüsse */
/* die MC-Simulation im Pegel mit der echten Student-t Verteilung übereinstimmen */
/* Später(drittletzte Zeile) wird für das Intervall -3 - +3 auf die Norm 0.904 normiert, der Wert kann student-t Tabellen entnommen werden */
normlist(lst,norm) :=(block(a:0.0, in:0), for in: 1 step 1 thru length(lst) do (a:a +lst[in]),
for in: 1 step 1 thru length(lst) do (lst[in]: norm*lst[in]/a));
/* Diese Funktion zieht "anz" standardnormalverteilte Zahlen, und gibt eine liste mit zwei Elementen zurück */
/* ertes Listenelement der Returnliste ist der Mittelwert, das zweite die empirische Standardabw. */
ggs_m(anz):= block(x:0, a:0, ims:0, mitt:0.0, loclist:makelist(0.0,x,1,anz),
retlist:makelist(0.0,x,1,2), for ims:1 step 1 thru anz do(loclist[ims]: gaussdm()),
for ims:1 step 1 thru anz do(a: a+loclist[ims]), retlist[1]: a/anz,
retlist[2]: std1(loclist),retlist );
/* Diese Funktion ermittelt den Abstand des wahren Mittelwerts der Standardnormalvt. */
/* IN EINHEITEN DER EMPIRISCHEN Standardabweichung(nicht der wahren Standardabweichung!) */
/* vom Mittelwert der Stichprobe. */
/* Dies bildet die Schätzung des Mittelwertfehlers gegenüber der Grundgesamtheit aufgrund nur einer Stichprobe ab */
/* und soll damit Student-t verteilt sein. */
gme_m(anz):= block(l1:makelist(0,x,1,2), l1:ggs_m(anz), a:-l1[1]*sqrt(3)/l1[2]);
/* Mach das viele, viele, viele Male für den Stichprobenumfang 3 (2 Freiheitsgrade)*/
/* incrementiere das vom MonteCarlo-Schuss getroffene Tabellenelement von "t_carlo" */
/* bilde ab und zu eine normierte Version der t-carlo-Liste (n_tcarlo)und plotte sie zusammen mit der echten Student-t-Verteilung */
for ii:1 thru 400 do
block( for iz: 1 step 1 thru (1000 + 6*ii) do
( a: gme_m(3), indx: 240 + floor(0.5+80*a), if ((indx > 0) and (indx <= 481)) then t_carlo[indx]:t_carlo[indx] +1.0 ),
n_tcarlo: copylist(t_carlo),
normlist(n_tcarlo,80*0.904),
plot2d([[discrete,xval,n_tcarlo], [discrete,xval,tru_t]],[legend,"MC_Sim","student_t"]))$,
);