Abb. 3
[Seminarübersicht] ... [Einführung in OMT] ... [Das dynamische Modell]
Das Objektmodell beschreibt die Struktur der Objekte in einem System, einschließlich ihrer Identität, Relationen zu anderen Objekten, Attribute und Operationen.
Ausgewählte Notationen der Objektdiagramme (grafische Repräsentation des Objektmodells) werden in diesem Abschnitt vorgestellt.

Abb. 3
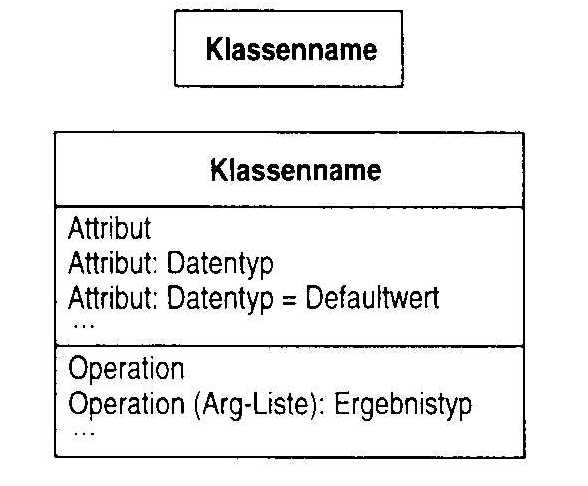
Eine Klasse wird durch ein Rechteck dargestellt, in dem es bis zu drei Bereiche geben kann.
Der erste Bereich enthält den Klassennamen.
Der zweite Bereich enthält die Attribute der Klasse. Optional können Datentyp und ggf. Defaultwerte angegeben werden.
Der dritte Bereich enthält die Operationen (Funktionen, Prozeduren) der Klasse. Auch hier können optional der Ergebnistyp (bei Funktionen) und die Argumentenliste angegeben werden.
Je nach gewünschtem Detailiertheitsgrad können der zweite und dritte Bereich angegeben oder weggelassen werden.
Um Testfälle (Szenarios) zu dokumentieren und Beispiele zu diskutieren ist es möglich, auch ein Instanzendiagramm zu erstellen. Ein Instanzendiagramm beschreibt konkrete Ausprägungen einer Klasse. Im Normalfall werden Klassen- und Instanzendiagramme nicht miteinander vermischt.
Die Notation für Instanzen ist in Abb. 4 dargestellt. Neben dem Klassennamen, in runden Klammern, können optional die konkreten Ausprägungen der Attribute angegeben werden.
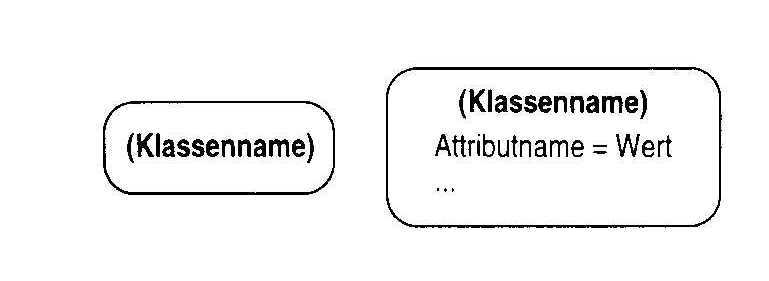
Abb. 4
Eine Verknüpfung ist eine physikalische oder konzeptionelle Verbindung zwischen zwei (oder mehreren) Objektinstanzen. Eine Assoziation beschreibt eine Gruppe dieser Verknüpfungen mit gleicher Struktur und gleicher Bedeutung (vgl. Unterschied zwischen einer Instanz und einer Klasse).
Eine Assoziation beschreibt eine Beziehung zwischen zwei (oder mehreren) Klassen und wird mit einer Verbindungslinie zwischen den Klassen im Objektdiagramm wiedergegeben. Der Assoziationsname ist optional. Obwohl der Assoziationsname eine Richtung andeuten mag, ist die Assoziation nicht gerichtet, sondern kann von beiden Seiten her betrachtet werden. In Abb. 5 ist die allgemeine Notation einer binären Assoziation angegeben. Weiter unten wird noch die Notation für eine triäre bzw. n-äre Assoziation vorgestellt werden.

Abb. 5
Rollennamen beschreiben ein Ende einer Assoziation. Die Angabe eines Rollennamen ist im allgemeinen optional. Lediglich für den Fall, daß eine Assoziation auf die selbe Klasse ausgedrückt werden soll, ist die Angabe des Rollennamens zwingend notwendig. Die Bedeutung der Rollennamen werden in den folgenden Beispielen ersichtlich werden.
Die Multiplizität spezifiziert, wieviele Instanzen einer Klasse mit einzelnen Instanzen der assoziierten Klassen in Beziehung stehen können. Dies ist vergleichbar mit den 1:1, 1:n und m:n Beziehung in einem ER-Modell. Die möglichen Symbole sind in Abb. 6 dargestellt.
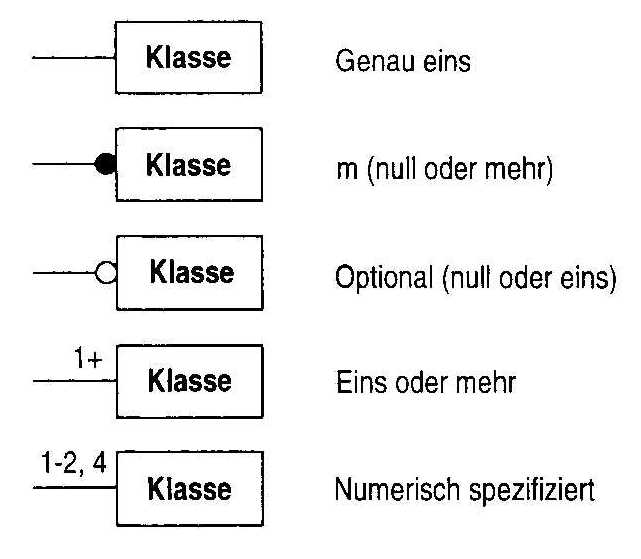
Abb. 6
Verknüpfungsattribute sind Eigenschaften (Attribute) der möglichen Verknüpfungen einer Assoziation. Die Notation für Verknüpfungsattribute ist in Abb. 2 dargestellt. Sofern auf eine Verknüpfung auch Operationen ausgeführt werden sollen, können die Verknüpfungsattribute auch als eigenständige Klasse modelliert werden. In diesem Fall würde der erste Bereich des Rechteckes für die Verknüpfungsattribute mit dem Klassennamen beschrieben werden.
Bei 1:n bzw. bei 1:1 Assoziationen ist es grundsätzlich möglich, die Verknüpfungsattribute einer Klasse (der "1"-Seite) zuzuordnen. Jedoch wird von diesem Vorgehen abgeraten.
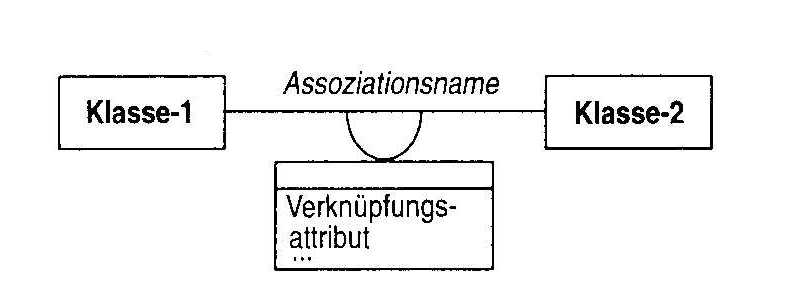
Abb. 7
In Abb. 8 ist die allgemeine Notation für eine Assoziation angegeben, an der drei Klassen beteiligt sind. Das Symbol für drei- oder mehrstelligere Assoziationen ist eine Raute. Im allgemeinen sind mehr als 3-stellige Assoziationen nicht notwendig. Sollten sie wider Erwarten dennoch in einem Modell auftreten, so sollte das gesamte Modell noch einmal kritisch betrachtet werden. Auch die 3-stelligen Assoziationen sind sehr selten.
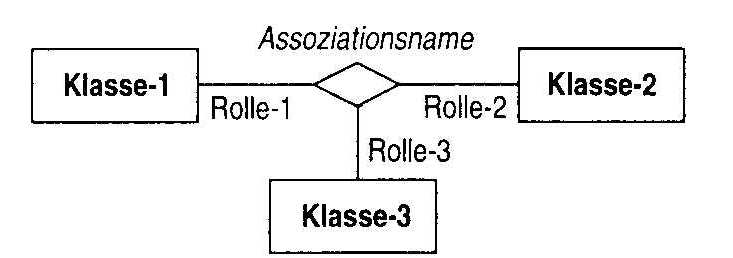
Abb. 8
Abb. 9 ist ein Beispiel für eine 2-stellige Assoziation zwischen den Klassen Person und Firma. Sowie einer rekursiven Assoziation auf die Klasse Person. Für die rekursive Assoziation sind die Rollennamen Chef und Mitarbeiter zwingend anzugeben, da sonst die Enden der Assoziation nicht eindeutig unterscheidbar wären. Die Assoziation Arbeitet-für hat als Verknüpfungsattribute Gehalt und Tätigkeitsbezeichnung und das Multiplizitätssymbol drückt aus, das jede Person genau für eine Firma arbeitet und jede Firma ein oder mehrere Personen beschäftigt.
Die Assoziation managt drückt eine Vorgesetzten-Hierarchie aus. Die Multiplizitätssymbole zeigen, daß eine Person in der Rolle des Chefs einen oder mehre Personen in der Rolle als Mitarbeiter managt. In der Hierarchie wird es eine Person geben - der oberste Chef sozusagen - der keinen weiteren Vorgesetzten hat. Dies wird durch die optionale Multiplizität (0 oder 1), als nicht ausgefüllter Kreis ausgedrückt. Auch die Assoziation managt besitzt ein Verknüpfungsattribut Leistungsbewertung.
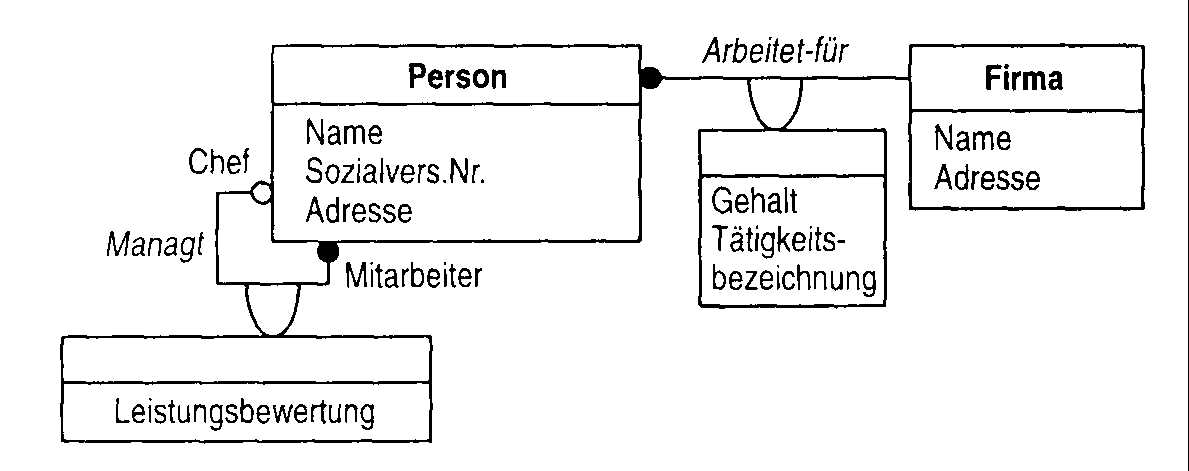
Abb. 9
Abb. 10 dient als Beispiel für eine triäre Assoziation der Objektklassen Team, Werfer und Jahr. Die Verknüpfungsattribute geben eine Sieg-Niederlagen-Statistik wieder. Folgende Zusammenhänge werden modelliert: Ein Werfer kann in einem Jahr in unterschiedlichen Teams spielen( z.B. Harry Eisenstat, 1939), die Statistiken für einen Werfen im selben Team kann für unterschiedliche Jahre geführt werden ( Willis Hudlin bei den Cleveland Indians) und in einem Jahr können unterschiedliche Kombinationen von Werfer und Team (z.B. für das Jahr 1940) auftreten. Diese Assoziation kann man nicht auf mehrere zweistellige Assoziationen herunterbrechen.
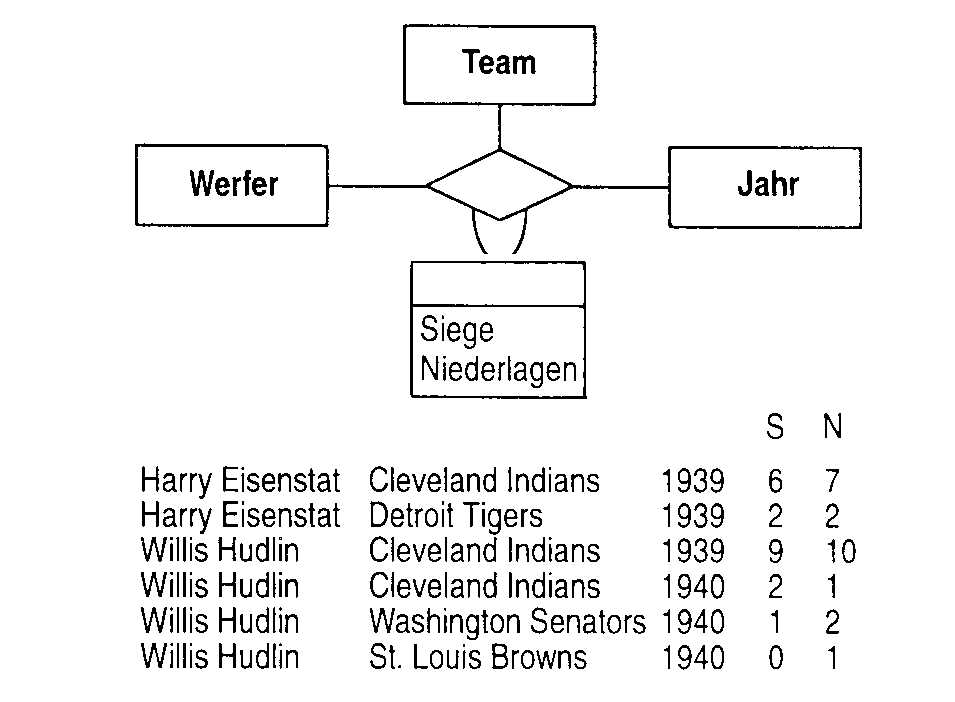
Abb. 10
Eine qualifizierte Assoziation setzt 2 Objektklassen mit Hilfe einer Qualifikationsangabe zueinander in Beziehung. Die Qualifikationsangabe ist ein zusätzliches Attribut, das die effektive Multiplizität einer Assoziation reduziert. 1:n und m:n Assoziationen können dadurch näher qualifiziert werden. Die Notation ist in Abb. 11 angegeben. Eine qualifizierte Assoziation kann auch als eine Art ternäre Assoziation betrachtet werden. Durch die Qualifikationsangabe wird die semantische Genauigkeit und die Übersichtlichkeit von Navigationspfaden erhöht.
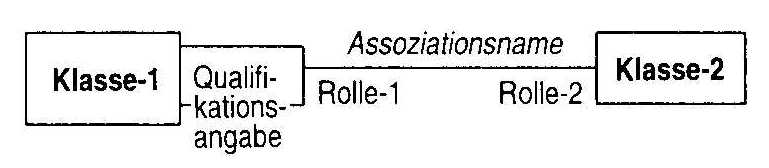
Abb. 11
In Abb. 12 wird eine qualifizierte Assoziation einer fast gleichwertigen unqualifizierten Assoziation gegenübergestellt. Die nicht-qualifizierte Assoziation modelliert den Sachverhalt, daß eine Firma an verschiedenen Börsen notiert sein kann. Das Börsenkürzel ist ein Attribut der Firma und ist somit an allen Börsen gleich.
Durch die qualifizierte Assoziation ist es möglich, das eine Firma an unterschiedlichen Börsen unterschiedliche Börsenkürzel besitzen kann, da das Börsenkürzel kein festes Attribut der Firma mehr ist. Über die Angabe einer bestimmten Börse zusammen mit dem Börsenkürzel als Qualifikationsangabe wird auf genau eine Firma zugegriffen. Dennoch bleibt der Sachverhalt, daß an einer Börse viele verschiedene Firmen notiert werden können - wie dies auch bei der nicht-qualifizierten Assoziation dargestellt wird - bestehen.

Abb. 12
Aggregation ist die "Teil-Ganzes" oder "ist-Teil-von" Relation, in der Klassen als Komponentenklasse einer Komponentengruppenklasse fungieren. Die Aggregation ist somit eine Sonderform der normalen Assoziation. Als wichtigsten Merkmal der Aggregation ist die Transitivität zu erwähnen. Wenn A ein Teil von B ist und B ein Teil von C, dann ist auch A ein Teil von C, wobei A, B und C Objektklassen darstellen sollen.
Oft ist es nicht leicht zu unterscheiden, ob es sinnvoll ist, einen Sachverhalt mit Hilfe von einer normalen Assoziation, einer Aggregation oder aber auch mit Hilfe der Generalisierung zu modellieren.
Die Notation für eine Aggregation wird in Abb. 13 dargestellt. Die bekannten Multiplizitätssymbole können auch hier verwendet werden.
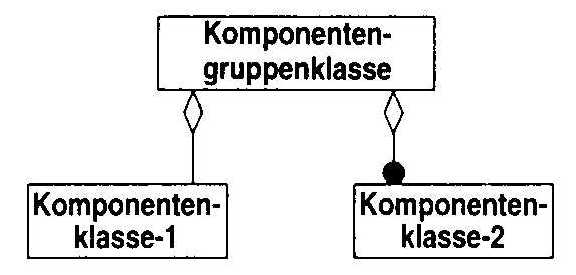
Abb. 13
Die Komponentengruppenklasse Mikrocomputer mit ihren entsprechenden Komponenten wird in Abb. 14 dargestellt. Aus dieser Abbildung wird auch ersichtlich, daß die Aggregation über mehrere Ebenen geführt werden kann. So besteht ein Mikrocomputer aus mindestens einem oder mehren Bildschirmen, optional einer Maus, genau einer Tastatur und einer Systemeinheit, die wiederum aus verschiedenen Komponenten zusammengesetzt ist.
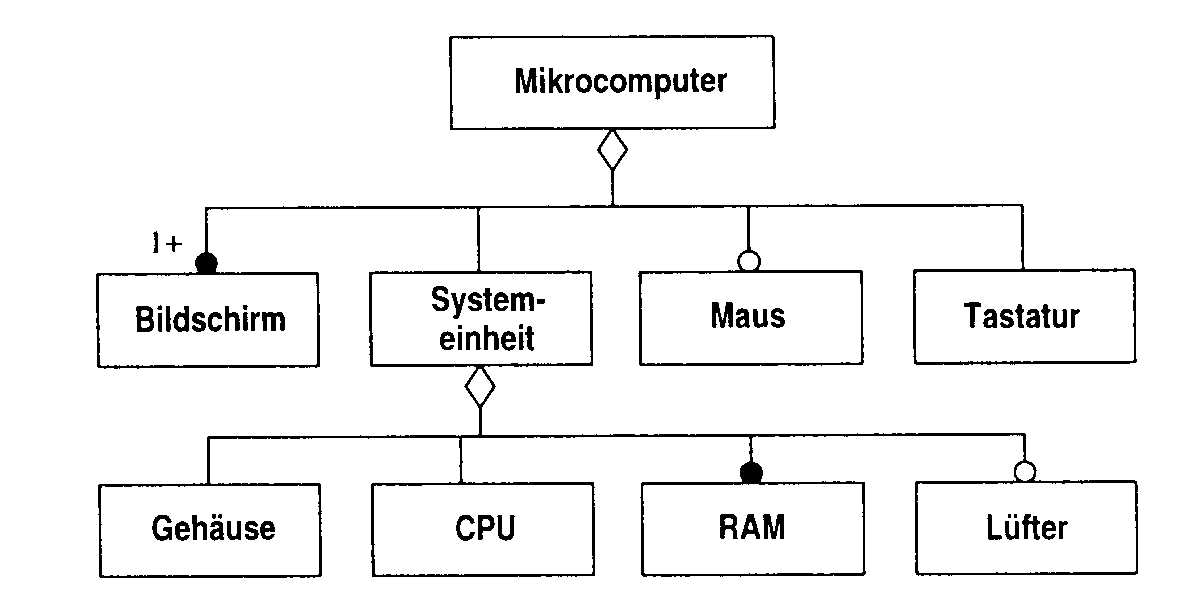
Abb. 14
Die Generalisierung ist die Beziehung einer Oberklasse und einer oder mehrern Unterklassen, die Verfeinerungen der Oberklasse darstellen. Attribute und Operationen, die für die Unterklassen gleich sind, werden als Attribute und Operationen der Oberklasse angegeben. Die Unterklassen übernehmen die Attribute und Operationen der Oberklasse und werden durch weitere Attribute und Operationen ergänzt. Es ist auch möglich, das in einer Unterklasse Attribute oder Operationen der Oberklasse überschrieben bzw. redefiniert werden.
Die allgemeine Notation für die Generalisierung (Vererbung) ist in Abb. 15 dargestellt. Auch Mehrfachvererbungen (eine Unterklasse erbt von mehr als einer Oberklasse) kann hiermit dargestellt werden. Optional kann an das Dreieck, welches die Generalisierung darstellt ein sogeannter Diskriminator (nicht in der Abb. ersichtlich) angegeben werden, der angibt, welche Eigenschaft der Oberklasse durch die Generalisierung verfeinert wird (vgl. Abb. 16: Diskriminator Dimensionalität).
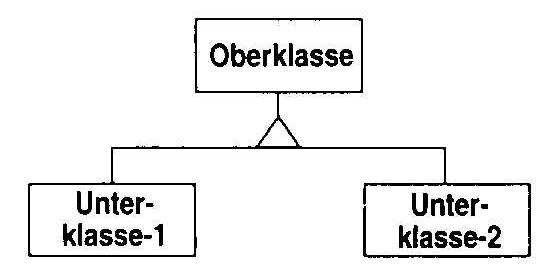
Abb. 15
In Abb. 16 wird das beliebte Beispiel für die Vererbungshierachie geometrischer Figuren dargestellt.
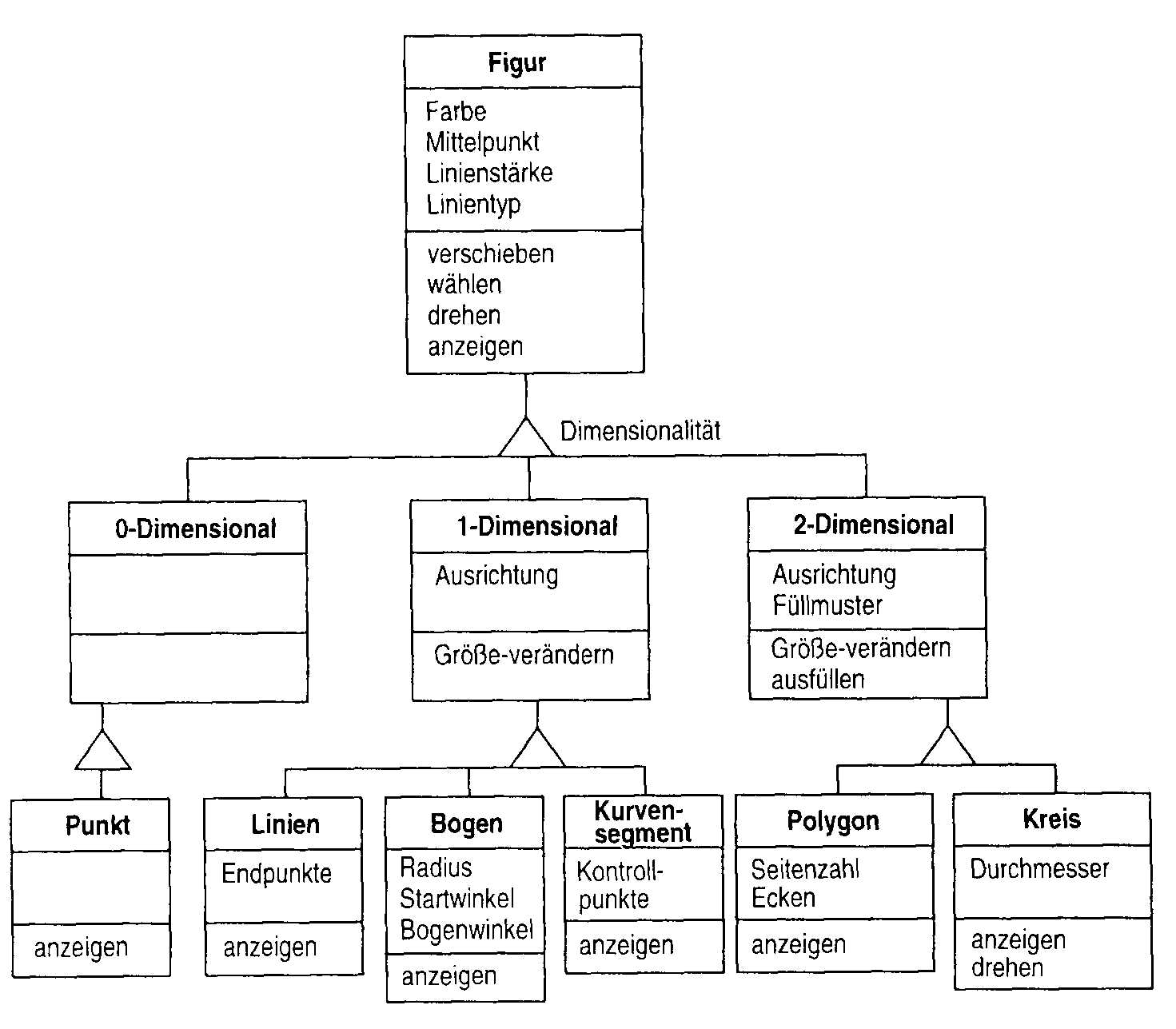
Abb. 17 soll einen Eindruck auf ein größeres Zusammenhängendes Objektmodell vermitteln. Es ist ein Objektmodell für ein Fenstersystem (bspw. Windows) in stark vereinfachter Form.
Das Objektmodell beschreibt die statische Struktur von Objekten, Klassen und ihren Relationen zueinander.
Ein Objekt ist ein konzeptuelles Mittel der Abstraktion von realen Sachverhalten in der Anwendungsdomäne.
Eine Verknüpfung ist eine Relation zwischen mindestens zwei Objekten (Instanzen) eine Assoziation ist eine Relation zwischen mindestens zwei Klassen.
Weitere Modellierungskonstrukte sind: Verknüpfungsattribute (-klassen), Rollen, Qualifikationsangaben, Generalisierungen und Aggregation.
Objektmodelle müssen anfänglich oft überarbeitet werden. Oft werden Objektmodelle verfeinert und überarbeitet, wenn die anderen Modelle - das dynamische und das funktionale Modell - erstellt worden sind. Der ganze Prozeß der Modellerstellung ist somit iterativ zu sehen.
Objektmodelle sind zusätzlich in Form eines Data Dictionary noch umgangssprachlich zu dokumentieren.
Nicht alle möglichen Konstrukte der OMT-Methodologie müssen in einem Objektdiagramm verwendet werden. In diesem Seminar wurden einige ausgewählte Notationen vorgestellt. Diese Übersicht ist daher bei weitem nicht vollständig. Es gibt noch eine Fülle von weiterführenden Konzepten für die Erstellung von Objektdiagrammen.
Grundsätzlich sind Objektmodelle so einfach wie möglich zu halten. Implementierungsdetails wie z.B. Pointer, die für die Implementierung einer Assoziation benutzt werden können, sollen in Objektmodellen nicht als Klassenattribute angegeben werden.
[Seminarübersicht] ... [Einführung in OMT] ... [Das dynamische Modell] ... [Seitenanfang]