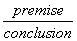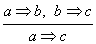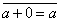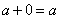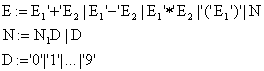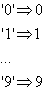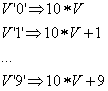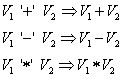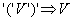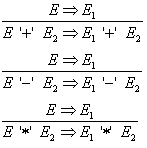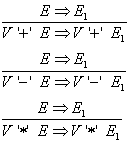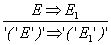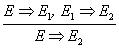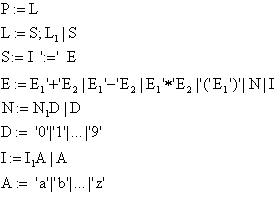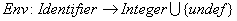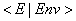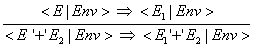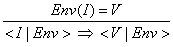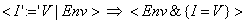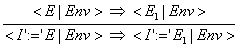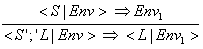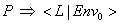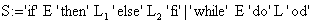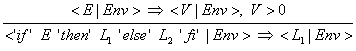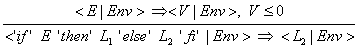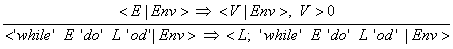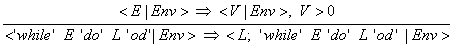Operationale Semantik der Beispielsprache

Übersicht: Operationale Semantik der Beispielsprache

• Abstrakte Maschine
• Inferenzregeln
• Arithmetische Ausdrücke
• Zuweisungen
• Kontroll-Anweisungen

Im Prinzip kann die abstrakte Maschine folgendermaßen dargestellt werden:

Sie enthält die drei Komponenten Programm, Steuerung und Speicher; die operationelle Semantik zeigt wie die Steuerung der abstrakten Maschine auf das Programm der zu definierenden Sprache reagiert und wie sich der Speicher dabei verändert. Anders gesagt: die operationelle Semantik ist der Effekt der Anwendung der abstrakten Maschine.

Wir werden eine bestimmte Form der abstrakten Maschine kennenlernen - die Reduktionsmaschine. Ihre Steuerung operiert direkt am Programm um es auf dessen semantischen Wert zu reduzieren. Um zu zeigen, wie die Steuerung der Reduktionsmaschine die Sprachkonstrukte zu einem Wert reduziert, werden wir die Reduktionsregeln spezifizieren --> Inferenzregeln.

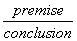
Die Prämisse oder die Bedingung steht oberhalb der Trennlinie, unter der Trennlinie steht dann die Konklusion oder das Resultat. Dies gibt an, dass wann immer die Prämisse wahr ist, ist die Konklusion auch wahr.

Beispiel:

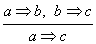
Axiome sind Inferenzregeln ohne Prämisse, sie sind immer wahr.
Schreibweise:

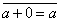
oder auch einfach:

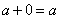
Wir benutzen diese Notation, um zu beschreiben wie die Steuerung einen Ausdruck zu einem Wert reduziert. Es gibt mehrere Schreibweisen für diese Regel; die bestimmte Form, die wir für unsere Reduktionregeln benutzen, wird strukturelle operationelle Semantik genannt. Eine Alternative dazu wäre die natürliche Semantik, die eigentlich der denotationellen Semantik näher kommt.

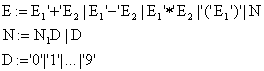
Weiter legen wir folgendes fest:

(1) Wir fassen alle Regeln, die eine Ziffer zum entsprechenden Integerwert reduzieren, unter der ersten Regel zusammen. Diese Regeln sind Axiome:

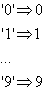
(2) Unter der zweiten Regel sind alle Regeln zusammengefasst, die eine Zahl zu einem Integerwert reduzieren - Axiome:

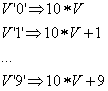
(3-5) Ein Ausdruck der aus zwei Integerwerten und einem Operator-Symbol besteht, kann durch Anwenden der entsprechenden Operation zu einem Wert reduziert werden - Axiome:

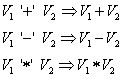
(6) Besteht ein arithmetischer Ausdruck aus einem in Klammern eingeschlossenen Integerwert, können die Klammern gelöscht werden - Axiom:

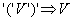
(7-9) Besteht ein Ausdruck aus zwei Teilausdrücken und einem Operator-Symbol, so kann der linke Teilausdruck E durch E1 ersetzt werden, wenn E impliziert E1:

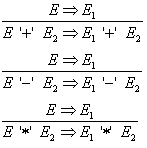
(10-12) Besteht ein Ausdruck aus zwei Teilausdrücken und einem Operator-Symbol, wobei der linke Teilausdruck bereits zu einem Integerwert reduziert wurde, so kann der rechte Teilausdruck E durch E1 ersetzt werden, wenn E impliziert E1:

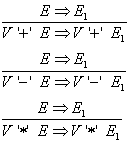
(13) Besteht ein Ausdruck aus einem in Klammern eingeschlossenen Ausdruck, so kann dieser Ausdruck E durch E1 ersetzt werden, wenn E impliziert E1:

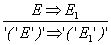
(14) Diese Regel besagt einfach, dass die Auswertung bzw. Reduktion eines Ausdrucks schrittweise erfolgen kann:

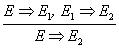
Beispiel:

Wir wenden die Reduktionsregeln an, um den Ausdruck: 2 * (3 + 4) - 5 auf dessen Wert zu reduzieren. Um jeden Reduktionsschritt genau zu zeigen, setzen wir die einzelnen Zeichen in Hochkommata. Wir fangen mit der Reduktion des Teilausdrucks: 3 + 4 an:

Wir haben gezeigt, dass die Reduktionsmaschine den Ausdruck 2 * (3 + 4) - 5 zu 9 reduzieren kann. 9 ist der Wert des Ausdrucks.

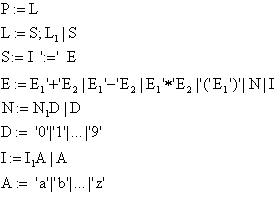
Da die Zuweisungen den Speicher verändern, müssen wir den Speicher bei der Spezifikation der Reduktionsregeln mit einbeziehen; dabei betrachten wir den Speicher als eine Umgebung bzw. unsere Fuktion Environment von Bezeichner nach Integerwerte. Wir erinnern uns an die Notation:

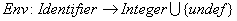
Um die Abhängigkeit eines Wertes von der Umgebung zu kennzeichnen, benutzen wir folgende Notation:

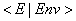
Wir sagen: E wird in der Umgebung Env ausgewertet.
Die Regeln, die wir zuvor für die arithmetischen Ausdrücke definiert haben, ändern sich dann entsprechend. Beispiel - Regel 7:

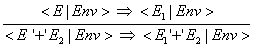
Wir definieren die zusätztlichen Reduktionsregeln für die Zuweisungen:

(15) Diese Regel ist für den Fall, dass ein Ausdruck ein Bezeichner ist. In diesem Fall wird der Bezeichner I zum Integerwert V ausgewertet, wenn I in der Umgebung (Speicher) gleich V ist:

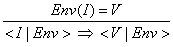
(16) Die Zuweisung eines Wertes V zum Bezeichner I wird zu einer neuen Umgebung reduziert, wo I gleich V ist (Verändern des Speichers) - Axiom:

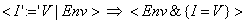
(17) Die Reduktion eines Audrucks innerhalb einer Zuweisung. E kann durch E1 ersetzt werden, wenn E impliziert E1.

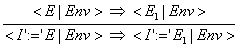
(18) Wenn das Statement (Zuweisung) S zu einer neuen Umgebung Env1 reduziert wird, wird die Statement-Liste auf den Rest der Liste reduziert, die dann in der neuen Umgebung Env1 ausgewertet wird. Es werden also die Statements aus der Statement-Liste nacheinander abgearbeitet; so wird schließlich die Statement-Liste zu einer neuen Umgebung reduziert:

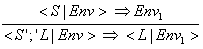
(19) Ein Programm ist schließlich nichts anderes als eine Statement-Liste und die Umgebung ist erstmal leer - Axiom:

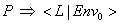
Beispiel:

So haben wir unser Beispielprogramm zu einer Umgebung {a = 15, b = 20} reduziert.

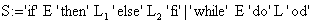
(20) Wenn die Bedingung 8Ausdruck E9 zu einem Wert ausgewertet wurde und wenn dieser Wert größer 0 ist, so wird die if-Anweisung zu der Statement-Liste L1 reduziert.

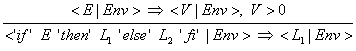
(21) Wurde die Bedingung zu einem Wert kleiner 0 ausgewertet, wird die if-Anweisung zu der Statement-Liste L2 reduziert

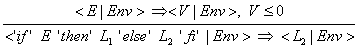
(22) Wenn die Bedingung der while-Anweisung zu einem Wert kleiner 0 ausgewertet wurde, dann wird die while-Anweisung einfach zu der Umgebung Env reduziert.

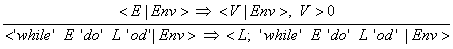
(23) Wenn die Bedingung zu einem Wert größer 0 ausgewertet wurde, wird die while-Anweisung zu der Statement-Liste L, gefolgt von der while-Anweisung, reduziert - diese Regel ist rekursiv:

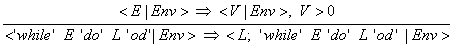
Beispiel:

Die endgültige Umgebung ist {n = -3, i = 0, fact = 6}