Typüberprüfung und Polymorphie
... [ Seminar "Programmierkonzepte und Programmiersprachen"]
... [ Inhaltsübersicht ]
... [ zurück ] ... [ weiter ]
Übersicht: Typüberprüfung und Polymorphie
Vorteile der Hindley-Milner Typüberprüfung
Ein Vorteil wurde mit der Typinferenz im letzten Kapitel bereits angesprochen. Die Möglichkeit
Typinformation wegzulassen hat aber nicht nur Vorteile, da es oft sinnvoll ist Typinformationen aus
Dokumentationsgründen in den Programmcode zu schreiben.
Ein weitaus grösserer Vorteil ist, dass beim Hindley-Milner System Typen so allgemein wie möglich
sein können und trotzdem stark auf Konsistenz geprüft werden.
Polymorphe Typen
Polymorph kommt aus den Griechischen und heisst übersetzt "mehrere Formen habend".
In Programmiersprachen sind damit Bezeichner gemeint, die (gleichzeitig) mehrere Typen haben können.
Ein Beispiel wären hier zum Beispiel overloaded Funktionen. Hierbei gibt es eine meist kleine endliche
Menge von Typen, die durch die verschiedenen Deklarationen gegeben sind. Diese Art von Polymorphismus nennt
man ad hoc Polymorphismus.Ad hoc ist lateinisch und bedeutet "zu diesen Zweck". Mit den Namen wird
die Tatsache beschrieben, dass die überladenen Funktionen jeweils mit einem bestimmten Hintergedanken
eingeführt werden. In ML gibt es nicht die Möglichkeit Funktionen zu überladen, während
dies in Haskell möglich ist.
Eine weitere sehr bekannte Art von Polymorphismus findet man in objektorientierten Sprachen, wo Objekte, die
den selben Vorfahren besitzen, gleiche Operationen teilen oder auch redefinieren. Diese Art des Polymorphismus
nennt man reiner Polymorphismus oder Subtyppolymorphismus.
Eine dritte Art wird parametrischer Polymorphismus genannt und spielt eine wichtige Rolle bei der Hindley-Milner
Typüberprüfung. Wie schon in vorrangegangenen Beispielen gesehen ordnet die Typüberprüfung implizit
Typvariablen Ausdrücken zu, für die explizit kein Typ deklariert wurde.
Beispiel: a[i] = b[i]
1. Schritt: Die Typüberprüfung wird dem i den Typ Integer zuordnen, da dies der erwartete Typ für den
Index von arrays ist.
Des weiteren schliesst er darauf, dass a und b arrays sind mit noch nicht bekannten Basistypen &alpha und &beta.
2. Schritt: Da es sich bei dem Codestück um eine Zuweisung handelt, schliesst die Typüberprüfung
darauf, dass die beiden Basistypen gleich sein müssen(&alpha == &beta), damit kein Typfehler vorliegt. Im Laufe
der Unifikation werden nun alle arrays of &beta durch array of &alpha ersetzt.
3. Das &alpha wurde nicht weiter spezifiziert und kann potentiell unendlich viele Typen annehmen.
Man kann &alpha somit als Typparameter ansehen, woher auch der Name parametrischer Polymorphismus herkommt.
Diese Art des Polymorphismus geschieht implizit im Laufe der Typüberprüfung und wird deswegen auch
impliziter parametrischer Polymorphismus genannt. In ML und Haskell kann der Programmierer Typparameter auch selbst
deklarieren. Dies nennt man dann entsprechend expliziter parametrischer Polymorphismus.
Polymorphe Funktionen
Eine besonders mächtige Art des parametrischen Polymorphismus sind
die Polymorphen Funktionen. Diese Art des Polymorphismus soll wiederrum
mit einen kleinen Beispiel erklärt werden.
Beispiel:
int max (int x, int y)
{ return x > y ? x : y; }
Besonderheiten dieser Funktion:
-Der Körper der Funktion ist immer gleich, egal welchen arithmetischen Typ die Parameter besitzen.
-Für alle diese Typen muss allerdings der Grösser-als-Operator "<" definiert sein.
-Der "<"-Operator selbst ist auch overloaded für verschiedene Typen.
Um die Abhängigkeit der Funktion von den Typen ihrer Parameter zu verringern, kann man einen weiteren Parameter
einführen, der die Grösser-als-Funktion repräsentiert.
int max (int x, int y, int (*gt)(int a,int b))
{ return gt(x,y) ? x : y; }
In einen weiteren Schritt lässt man die Typangaben weg.
int max (x,y,gt)
{ return gt(x,y) ? x : y; }
In ML wäre dies legaler Code.
fun max (x,y,gt) = if gt(x,y) then x else y;
Der entsprechende Syntaxbaum mit den internen Typbezeichnern:
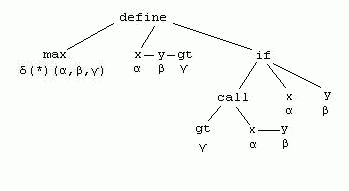
Dieses Beispiel ist wiederum in C-Syntax gehalten.Max ist eine Funktion mit 3 Parametern(α,β,γ)
und hat als Resultat den Typ δ.Bei der Typüberprüfung wird als erstes der Knoten mit dem
Funktionsaufruf untersucht.
Gt ist eine Funktion mit 2 Parametern α und β und hat als Resultat den Typ ε.
Daraus folgt, dass γ = ε(*)(α,β) ist. &gamma wird daraufhin mit ε(*)(α,β)
im gesamten Syntaxbaum unifiziert. Dem Funktionsaufrufs-Knoten wird als Typ ε zugeordnet, welcher ja
der Resultattyp der gt-Funktion ist.
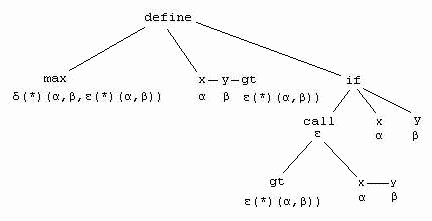
In einen nächsten Schritt wird der "if"-Knoten ausgewertet. Der if-Ausdruck zeichnet sich dadurch aus,
dass der Testausdruck typischerweise vom Typ boolean ist und die Typen des then und else Teils gleich sind.
Um diese Signatur zu erfüllen folgt daraus zwingendermassen, dass α=β=δ und ε vom Typ
boolean ist. β und δ werden also mit α unifiziert und ε mit boolean instantiiert.
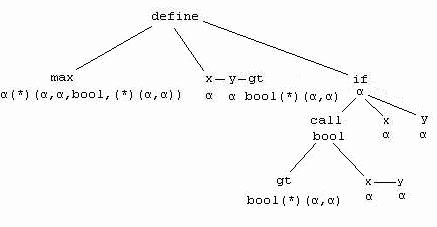
δ wurde mit α unifiziert, da das Resultat des if-Ausdrucks α ist und dieser der Typ des
Funktionsrumpfes und somit des Resultattyps der max Funktion ist.Max ist also vom Typ
α(*)(α,α,bool(*)(α,α)).
α kann hierbei jeden Typ annehmen und ist damit ein Typ-Parameter.
In ML kann man diesen Typ folgendermassen schreiben:
'a * 'a *('a * 'a -> bool) -> 'a
"'a" wird hier für die Typvariable α benutzt.Der Pfeil "->" steht für einen
Funktionstyp. Die Parameter werden als kartesisches Produkt dargestellt, welches in ML durch das "*"
gekennzeichnet wird. Das kartesische Produkt von A und B wird demnach "A*B" geschrieben und die Werte
dieses Typs werden als Tupel "(a,b)" dargestellt, wobei "a" Element von "A" und
"b" Element von "B" ist.
Durch diese Form der Typisierung kann man die Funktion max nun in jeder Situation anwenden, in der die
tatsächlichen Typen mit dem polymorphen Typ vereint werden kann.(Unifikation)
Beispiel in ML:
fun gti(x:int,y) = x > y;
fun gtr(x:real,y) = x > y;
fun gtp((x,y),(z,w)) = gti(x,z);
Aufrufe der max-Funktion:
max(3,2,gti);(*Ergebnis 3*)
max(2.1,3.2,gtr);(*Ergebnis 3.2)
max((2,"hello"),(1,"hi"),gtp);(*Ergebnis (2,"hello")*)
alpha (*) (alpha,alpha,bool (*) (alpha, alpha)) ist die allgemeinste Form für die max-Funktion,
der sogenannte Haupttyp. Jeder Aufruf der Funktion spezialisiert nun diesen Haupttyp zu einen monomorphen Typ, wobei
auch implizit die Typen der Parameter spezialisiert werden können.
Beispiel:
Der Typ der gtp-Funktion ist bool (*)((int,alpha),(int,beta)). Die Variablen y und w haben zwei
verschiedene Typparameter, da sie nicht im Körper der Funktion benutzt werden und so von einem beliebigen
Typ sein können.
Ruft man aber nun die max-Funktion auf, dürfen y und w keine verschiedenen Typen besitzen, da die
max-Funktion darauf besteht, dass die beiden ersten Parameter den gleichen Typ besitzen.
max((2,"hello"),(1,2),gtp); (* illegal! *)
Die max-Funktion spezialisiert in diesen Fall die gtp-Funktion auf den Typ
bool (*)((int,alpha),(int,alpha)).
Eine Erweiterung dieser Regel ist, dass jedes polymorphe Objekt, welches als Parameter an eine Funktion übergeben
wird, eine feste Spezialisierung für die Dauer der Funktion behält. Würde die gtp-Funktion nochmals
innerhalb der max-Funktion aufgerufen, würde sie die oben genannte Spezialisierung behalten.
Ist die Referenz auf die polymorphe Funktion hingegen nicht lokal, wird die Spezialisierung nicht eingeschränkt.
Beispiel:
fun ident x =x;
fun makepair (x,y) = (ident x, ident y);
makepair(2,3.2);
(* ok -- ident hat 2 verschiedene Typen, 1 für jeden Aufruf *)
Falsch hingegen wäre indent als Parameter zu übergeben:
fun makepair2 (x,y,f) = (f x, f y);
makepair2(2,3.2,ident);
(*Typfehler - ident darf in diesen Fall keinen allgemeinen Typ haben*)
Diese Restriktion nennt man im Hindley-Milner Typsystem let-bound Polymorphismus. Let-bound Polymorphismus erschwert
die Hindley-Milner Typüberprüfung, da man so Typvariablen in zwei Kategorien unterteilen muss.
Zu der ersten Kategorie gehören die Variablen, deren Wert überall der selbe ist und sich bei der
Spezialisierung/Instantiierung gemeinsam verändert.
Zu der zweiten Kategorie gehören die nichtlokalen Referenzen, die bei jeder Benutzung verschieden instanziert
werden können. Diese Art von Variable wird auch als generische Typvariable bezeichnet.
Ein weiteres Problem entsteht, wenn der Versuch gemacht wird eine Typvariable mit einen Typausdruck zu vereinen,
der die Typvariable selbst enthält.
Beispiel:
fun f(g) = g(f);
1. Schritt: g wird die Typvariable α zugewiesen und f der Typ "α -> β"
2. Schritt: Der Körper von f wird untersucht mit dem Ergebnis, dass g eine Funktion ist mit einem Parameter,
dessen Typ der von f ist, und als Rückgabewert den Rückgabewert von f hat.
3. Schritt: Folglich sollte α gleichgesetzt werden mit "(α -> β) -> β".
4. Schritt: Die Auflösung der Gleichung "α = (α -> β) -> β" führt allerdings
zu einer unendlichen Rekursion, da α sich selbst als Komponente enthält.
Um dies zu Vermeiden, muss die Typüberprüfung sicherstellen, dass die Typvariable nicht Teil des
Ausdrucks ist, mit der sie gleichgesetzt werden soll.Diesen Test nennt man occur-check. Er ist leider nur
schwer effizient auszuführen, aber für eine reibungslose Typüberprüfung unverzichtbar.
... [ Seminar "Programmierkonzepte und Programmiersprachen"]
... [ Inhaltsübersicht ]
... [ zurück ] ... [ Seitenanfang ]
... [ weiter ]



