Berechenbarkeit

Definition

In der Berechenbarkeitstheorie ist eine berechenbare Funktion als eine Funktion definiert, die von einem mechanischen Rechengerät (z.b. Computer) gelöst werden kann.

Diese Definition dient der präzisen Festlegung der Eigenschaften eines Algorithmus und als Grundlage für die Definition formaler Systeme zur Schlussfolgerung über die Berechenbarkeit von Problemen.

Ein solcher Algorithmus muss folgende Eigenschaften erfüllen:

1. Der Algorithmus besteht aus einer endlichen Menge einfacher und präziser Instruktionen.
2. Der Algorithmus terminiert immer nach einer endlichen Anzahl von Schritten.
3. Die Ausführung des Algorithmus erfordert neben dem Verständnis der Instruktionen keine weitere Intelligenz.
4. Der Algorithmus kann im Prinzip von einem Menschen allein mit Stift und Papier ausgeführt werden.

Für die Beschreibung solcher Algorithmen wurden diverse Formalismen entwickelt:

• Rekursive Funktionen
• Turing Maschinen
• λ-Kalkulus
• Registermaschinen
• Kombinatorische Logik
• Markov Algorithmen
• ...

All diese Formalismen besitzen bewiesenermaßen die gleiche Ausdruckskraft. Jeder Algorithmus, der durch einen Formalismus beschrieben werden kann, lässt sich ebenfalls in allen anderen Formalismen beschreiben.

Turing Maschinen

Die Turing Maschine, der wohl bekannteste Formalismus zur Beschreinung und Ausführung von Algorithmen, wurde in den 1930er Jahren von Alan M. Turing entwickelt.

Die Turing Maschine kann als ein minimaler Computer angesehen werden und besteht aus vier Komponenten:

• Einem Speicherband, bestehend aus Speicherzellen, die jeweils einen Wert eines endlichen Alphabets aufnehmen können. Das Alphabet besteht aus einem speziellen Leer Symbol und ein oder mehr weiteren Symbolen.
  Das Speicherband dehnt sich endlos in beide Richtungen aus. Eine Turing Maschine hat also immer ausreichend Speicherplatz zur Verfügung.
• Einem Kopf oder Zeiger, der Werte vom Speicherband lesen und darauf schreiben kann. Der Kopf kann Zellenweise nach links oder rechts bewegt werden.
• Ein Zustandsregister, dass den aktuellen Zustand der Turing Maschine speichert. Die Anzahl unterschiedlicher Zustände ist endlich und es gibt immer einen speziellen Zustand Start.
• Eine Übergangsfunktion oder Übergangstabelle, die für den aktuellen Zustand und den Inhalt der aktuelle Speicherzelle, einen neuen Speicherzellenwert, die Bewegungsrichtung für den Kopf und den Folgezustand angibt. Die Maschine hält an, wenn die Übergangstabelle keinen Eintrag für die aktuelle Kombination von Zustand und Speicherwert besitzt.

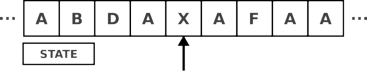
Aufbau einer Turing Maschine

Anmerkung: Alle Komponenten einer Turing Maschine sind endlich. Auch das Speicherband ist nicht endlos, sondern enthält nur mindestens so viele Speicherzellen, wie für die Ausführung des Algorithmus notwendig sind.

Trotz ihres minimalen Aufbaus ist die Turing Maschine erstaunlich ausdrucksstark. Jeder konventionelle Algorithmus (d.h. jedes auf einem Computer umsetzbare Programm) kann ebenso auf einer Turing Maschine umgesetzt werden.