[Informatik-Seminar WS2004/05] [Inhalt] [Zurück] [Weiter]
In diesem Kapitel wird das Arbeiten mit Listen erläutert. Die Liste ist in Scheme (bzw. LISP) eine Möglichkeit Daten zu strukturieren. Dies ist vollkommen ausreichend, da man in Listen alle Arten von Elementen, egal welchen Typs, speichern kann.
Der Umgang mit den Listen wird hier anhand von praktischen Beispielen erläutert. Abschließend wird ein Beispiel für einen einfachen Binären-Such-Baum dargestellt.
4.2 Beispiel: Binärer-Such-Baum
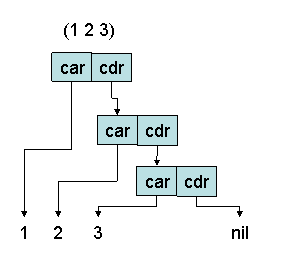
Listen sind bereits aus den vorherigen teilweise Kapiteln bekannt. Eine Liste entsteht durch die Kombination von mehreren Elementen. Scheme (und LISP) verwaltet eine Liste, indem die einzelnen Elemente verknüpft werden. Ein Element besteht aus einem car-Teil und einem cdr-Teil. Der car-Teil enthält einen Zeiger auf das jeweilige Element. Der cdr-Teil enthält einen Zeiger auf das nächste Element.
Die Liste mit den Elementen 1 2 und 3 wird also so dargestellt:

Hier ist das erste Elemente eine Liste (mit den Elementen 1 und 2). Das zweite Element ist die 3.
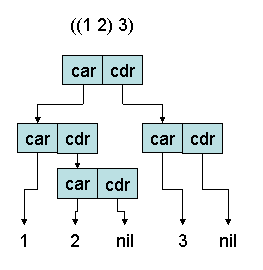
Für die folgenden Beispiele wird eine Daten-Liste definiert:
(define L '(1 2 3 4 5))
Zu beachten ist hier wieder das einfache Anführungszeichen, welches die Auswertung der Liste verhindert. Würde dies fehlen, würde Scheme als erstes Element eine Funktion erwarten.
Nun werden ein paar Standard-Funktionen definiert.
Dies liefert eine leere Liste:
(define emptylist '())
Um zu testen, ob eine Liste leer ist, wird folgendes definiert. Dazu wird die
Funktion null? verwendet.
(define (isempty L) (null? L))
Um aus einem Element E eine Liste zu erzeugen, kann die Funktion list
verwendet werden. Übergibt man mehrere Argumente an die Funktion list,
werden alle zusammen zu einer List.
(define (makelist E) (list E))
Um ein Element E vor eine vorhandene Liste L zu hängen, gibt es die Funktion
cons.
(define (add E L) (cons E L))
Um auf die Elemente einer Liste zuzugreifen, gibt es die Funktionen car und
cdr. Car liefert immer das erste Argument einer Liste. Cdr
liefert den Rest der Liste. Um also auf das zweite Element einer Liste L
zuzugreifen, muss man erst cdr auf L anwenden und anschließend car.
Da solche Ausdrücke häufig vorkommen, gibt es dafür einzelne Funktionen. In
diesem Fall heißt diese dann cadr.
(define (head L) (car L))
(define (tail L) (cdr L))
(define (2nd L) (cadr L))
(define (2ndtoo L) (car (cdr L) ))
(define (3rd L) (caddr L))
Um auf ein beliebiges Element zuzugreifen, wird hier eine einfache Funktion definiert. Diese arbeitet rekursiv die Liste durch, bis dass gewünschte Objekt erreicht ist. Als Argument wird die Position in der Liste angegeben.
(define (Ith i L)
(if (= i 1)
(head L)
(Ith (- i 1) (tail L))))
Die folgende Funktion isin gibt an, ob ein Element E in einer
Liste L enthalten ist.
(define (isin E L)
(if (null? L)
#f
(if (= (head L) E)
#t
(isin E (tail L)))))
Die folgende Funktion isPartOf gibt an, ob L eine Teilmenge von
M ist. Sie überprüft also, ob jedes Element aus L in M vorkommt.
(define (isPartOf L M)
(if (isempty L)
#t
(and (isin (head L) M) (isPartOf (tail L) M) )))
Diese Funktion lässt sich auch verwenden, um zu testen, ob zwei Listen L und M die gleichen Elemente enthalten. Dazu wird folgende Funktion definiert:
(define (hasSameElements L M)
(and (isPartOf L M) (isPartOf M L)))
Nun wurden bereits mehrere Funktionen zum Arbeiten mit vorhandenen Listen erstellt. Zum Schluss folgen noch zwei Funktionen zum Erstellen und Verändern von Listen.
Die Funktion append hängt die Liste M an die Liste L.
(define (append L M)
(if (isempty L)
M
(add (head L) (append (tail L) M))))
Schließlich folgt noch die Funktion reverse, welche die Liste L
umdreht.
(define (reverse L)
(if (isempty L)
L
(append (reverse (tail L)) (makelist (head L)))))
In diesem Beispiel werden die Funktionen für einen Binären-Such-Baum erstellt. In dem Baum sollen Strings sortiert gespeichert werden. Danach sollen diese ausgegeben werden. Außerdem soll natürlich in dem Baum nach Daten gesucht werden können.
Der Baum besteht aus Knoten, welche jeweils die Daten und zwei Kindknoten
enthalten. Ein Knoten ist also eine Liste mit dieser Struktur: (Daten, linker
Kindknoten, rechter Kindknoten)
Dabei enthält der linke Teilbaum nur Daten, die kleiner sind, als die Daten im
Knoten. Der rechte Teilbaum enthält folglich nur größere Daten.
Zuerst wird eine Funktion definiert, um einen Knoten zu erstellen, der nur die Daten enthält.
(define (makeDataNode D) (list D emptylist emptylist))
Diese Funktion kann verwendet werden um einen Baum, mit einem Knoten zu erstellen.
(define (makeTree D) (makeDataNode D))
Ein Knoten mit Daten und Kindknoten wird so erzeugt:
(define (makeNode D L R) (list D L R))
Um auf die einzelnen Elemente eines Knoten zugreifen zu können, werden folgende Funktionen definiert:
(define (data B) (head B))
(define (leftchild B) (2nd B))
(define (rightchild B) (3rd B))
Nun hat man alle Funktionen, die benötigt werden, um Daten in den Baum einzufügen. Dies geschieht mit folgender Funktion:
(define (insert D B)
(if (isempty B) (makeDataNode D) ; wenn B leer ist, den Knoten erzeugen
(if (string=? D (data B)) B ; wenn B schon enthalten ist, den Baum zurückgeben
(if (string<? D (data B)) ; wenn kleiner, dann in den linken Teilbaum
(makeNode (data B) (insert D (leftchild B)) (rightchild B) )
(makeNode (data B) (leftchild B) (insert D (rightchild B)) )
))))
Um zu testen, ob Daten im Baum enthalten sind, kann folgende Funktion verwendet werden.
(define (isinTree D B)
(if (isempty B) #f ; wenn B leer ist, sind keine Daten enthalten
(if (string=? D (data B)) #t ; wenn die Daten gleich sind, #t
(if (string<? D (data B)) ; sonst entscheiden,
wo weitergesucht wird
(isinTree D (leftchild B))
(isinTree D (rightchild B)) ))))
Die sortierte Ausgabe des Baum ist nun ganz einfach:
(define (printSortTree B)
(if (isempty B)
'()
(begin
(printSortTree (leftchild B))
(display " ")
(display (data B))
(display " ")
(printSortTree (rightchild B)) )))
Zuletzt noch eine Funktion, die die Struktur des Baumes ausgibt. Hier werden zuerst die Daten gefolgt von den Teilbäumen ausgegeben.
; Diese Funktion gibt i Leerzeichen aus.
(define (prnSpaces i) (if (> i 0) (begin (display " ")(prnSpaces(- i 1)))) )
; Den Baum mit erkennbarer Struktur ausgeben.
; Das Argument i gibt an, wie viele Leerzeichen ausgeben werden sollen
(define (printTree2 B i)
(if (isempty B)
'()
(begin
(prnSpaces i)
(display "D:")
(display (data B))
(newline)
(prnSpaces i)
(display "L:")
(newline)
(printTree2 (leftchild B) (+ i 2))
(prnSpaces i)
(display "R:")
(newline)
(printTree2 (rightchild B) (+ i 2)))))
; Dies Funktion ruft der Anwender auf.
(define (printTree B) (PrintTree2 B 0) )
[Informatik-Seminar WS2004/05] [Inhalt] [Zurück] [Weiter] [Seitenanfang]