Zyklische Strukturen

 

... [ Seminar "Einführung in die funktionale Programmiersprache Haskell" ] ... [ Inhaltsverzeichnis ] ... [ Zurück ] ... [ Weiter ] ...

Übersicht: Zyklische Strukturen

Konzept

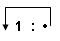
 Datenstrukturen wie Funktionen werden in der Programmierung oft rekursiv definiert. Als ein einfaches Beispiel soll die Funktion ones dienen, die eine unendliche Liste von Einsen als Resultat liefert.Ones kann deshalb auch als Synonym für diese unendliche Liste verwendet werden.
Definition: 
ones :: [Int]
ones = 1 : ones
Auswertung: 
ones = 1 : ones
ones = 1 : 1 : ones
ones = 1 : 1 : 1 : ones
usw. ...
Ausdrücke werden in Haskell bekanntlch aus Effizienzgründen bei der Auswertung intern als Graphen dargestellt. Die Darstellung der Funktion ones bzw. der aus dieser Funktion resultierenden unendlichen Liste als Graph ist insofern interessant, dass es sich um eine zyklische Struktur mit folgendem Aussehen handelt: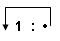
Bsp.:

Die vollständige unendliche Liste kann in dieser Darstellungsform mit einer konstanten Grösse an Speicherplatz realisiert werden. Als zweites Beispiel soll die folgende Definition betrachtet werden: 
more :: String
more = "More" ++ andmore
                 where andmore = "and more" ++ andmore
Beim Rückgabewert von more handelt es sich wiederum um eine eine unendliche Liste. Bei der Ausgabe des Funktionsergebnisses auf dem Bildschirm ergibt sich folgendes: 
? putStr more
More and more and more and more and more and more and m{Interrupted}
Die Darstellung von more erfolgt intern wiederum als Graph in Form einer zyklischen Struktur.
Bsp.:

weitere Beispiele mit zyklischen Stukturen:

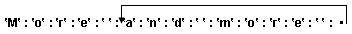
Die Funktion ones kann auch mit Hilfe der Funktion repeat realisiert werde.

Definition der Funktion repeat: 
repeat x :: α -> [α]
repeat x = x : reapeat x
Definition von ones mit Hilfe der Funktion repeat: 
ones = repeat 1
Die neue Definition von ones ist korrekt, jedoch liefert die Auswertung in diesem Fall keine zyklische Struktur. Die Ausgabe der ersten fünf Elemente würde nämlich folgendermaßen aussehen: 
1 : 1 : 1 : 1 : 1 : repeat 1
Dieser Graph ist nicht zyklisch, da bei jedem Auswertungschritt das Teilstück repeat 1 durch 1 : repeat 1 ersetzt wird. Um eine zyklische Struktur zu erhalten, müßte die Definiton von repeat in folgender Weise geändert werden: 
repeat x = xs where xs = x : xs
Im Folgenden soll noch einmal die Funktion iterate aufgegriffen werden, die bereits Gegenstand des vorangegangen Kapitels war. Auch diese Funktion läß sich auf unterschiedliche Arten definieren. Die ursprüngliche Definition verwendet wie im zuvor behandelten Beispiel ebenfalls keine zyklische Struktur. Durch eine abgewandelte Definiton läßt sie sich jedoch auch in eine zyklische Struktur wandeln. 
iterate f x = xs where xs = x : map f xs
Bei Auswertung der ersten Schritte des Ausdrucks iterate (2x) 1 ergibt sich folgendes Bild: 
iterate (2x) 1


Falls f x in O(1) Schritten ausgewertet werden kann, dann können die ersten n Elemente von iterate f x in O(n) Schritten berechnet werden.

Nun soll noch einmal der bereits angesprochene Effizienzvorteil von zyklischen Strukturen im Vergleich zu nicht zyklischen Strukturen betrachtet werden. Rückblickend auf die bereits bewiesene Gültigkeit der Gleichung 
iterate f x = x : map f (iterate f x)
sollen die Auswertungsschritte eines Aufrufes der Funktion iterate mit dieser Definition näher beleuchtet werden. 
iterate (2x) 1
=> 1 : map (2x) (iterate (2x) 1 )
=> 1 : 2 : map (2x) (map (2x) (iterate (2x) 1 ))
=> 1 : 2 : 4 : map (2x) (map (2x) (map (2x) (iterate (2x) 1 )))
Es ist deutlich zu erkennen, dass die Auswertung der ersten n Elemente in diesem Fall O(n²) Schritte benötigt. In Fällen wie diesen ist es also sehr wichtig zyklische Strukturen zu verwenden, um Effizienz zu wahren.

 

Das Hamming-Problem

 Hierbei handelt es sich um ein bekanntes Problem, welches auf den Mathematiker W. R. Hamming zurückzuführen ist. Es beschäftigt sich mit der Erstellung eines Programms, welches eine unendliche Zahlenliste mit den folgenden Eigenschaften erzeugt:

Unter Berücksichtigung dieser Restriktionen würde die Liste mit folgender Zahlenfolge beginnen: 
1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, ...
Das Hamming Problem gehört zu der Klasse der Hüllenproblemen.Hüllenprobleme spezifizieren in der Regel eine Sammlung von Initialisierungselementen und eine Klasse von generierenden Funktioen, die auf diese Elemente angewandt werden. Beim Hammingproblem wird die Hülle des Initialisierungselementes 1 unter Berücksichtigung der generierenden Funktionen (2×), (3×) und (5×) gesucht. Für das Hamming Problem existiert eine besonders effiziente Lösung, da sich die generierenden Funktionen monoton bezüglich (<) verhalten. Monoton bezüglich (<) bedeutet beispielsweise bei Nutzung der Funktion (2×), dass falls x < y gilt, auch 2 x < 2 y gilt. Der Schlüssel zur Lösung des Problems liegt in der Nutzung der Funktion merge. Diese Funktion erhält zwei unendliche Zahlenlisten in aufsteigender Ordnung als Argumente und überführt diese in eine unendliche Zahlenliste in aufsteigender Ordung ohne Duplikate.

Definition: 
merge :: [Integer] -> [Integer] -> [Integer]
merge (x : xs) (y : ys) | x < y  = x : merge xs (y : ys)
                        | x == y =   x : merge xs ys
						| x > y  =   y : merge (x : xs) ys
Unter Nutzung der Funktion merge ist es sehr einfach die Funktion hamming zur Lösung des Hamming Problems zu definieren. 
hamming :: [Integer]
hamming = 1 : merge (map (2×) hamming)
                    (merge (map (3×) hamming)
			               (map (5×) hamming))
Die Funktion hamming wird durch folgende zyklische Struktur dargestellt:

Nach Auswertung der ersten sieben Schritte ergibt sich folgendes Bild:

Die ersten n Elemente der Hamming Liste können in O(n) Schritten ermittelt werden. Im Folgenden soll eine Verallgemeinerung des Hamming Problems dargestellt werden. Das heißt, die Zahlen 2, 3, und 5 sollen durch die willkürlichen, aber positiven Zahlen a, b, c ersetzt werden. Eine Funktion die diese Anforderung erfüllt, ist die folgende:

Definition: 
hamming2 :: Integer -> Integer -> Integer -> [Integer]
hamming2 a b c = 1 : merge (map (a×) hamming2 a b c)
                           (merge (map (b×) hamming2 a b c)
						          (map (c×) hamming2 a b c))
Diese Lösung ist korrekt. Allerdings handelt es sich in diesem Fall um keine zyklische Struktur, was zu einer Anzahl von O(n) Auswertungsschritten für n Elemente führt. Eine effizientere, weil zyklische Struktur ist die folgende: 
hamming2 a b c = hamming3
                 where hamming3 = 1 : merge (map (a×) hamming3)
				                             merge (map (b×) hamming3)
											       (map (c×) hamming3))
... [ Seminar "Einführung in die funktionale Programmiersprache Haskell" ] ... [ Inhaltsverzeichnis ] ... [ Zurück ] ... [ Weiter ] ...