Lazy Evaluation
Übersicht: Lazy Evaluation
Reduktionsstrategien
Es existieren zwei im Ansatz unterschiedliche Reduktionsstrategien, die linkeste innerste Reduktion
(leftmost innermost reduction) und die linkeste äußerste Reduktion (leftmost outermost reduction).
Stellt man beide in einem ersten Vergleich gegenüber, z.B. bei der Evaluierung des Ausdrucks
square(3+4) erhält man diese Reduktionsfolgen:
01 {leftmost innermost reduction}
02 square(3+4)
03 = {definition of +}
04 square 7
05 = {definition of square}
06 7 x 7
07 = {definition of x}
08 49
09
10
|
01 {leftmost outermost reduction}
02 square(3+4)
03 = {definition of square}
04 (3+4) x (3+4)
05 = {definition of +}
06 7 x (3+4)
07 = {definition of +}
08 7 x 7
09 = {definition of x}
10 49
|
Auffallend ist, dass wir einen zusätzlichen Schritt bei der outermost reduction benötigen. Das Endergebnis einer vollständigen Reduktion
werden wir im folgenden als
Normalform bezeichnen. Es wird also kein reduzierbarer Ausdruck (
Redex, reduciable expression) mehr vorhanden sein.
Beispiele für die Normalform sind Konstanten oder Listen in der Form e1 : e2 : ... : en : []. Eine genaue Definition der Normalform wird durch
die Verwendung des sog.
Lambda-Kalküls
erzielt.
In einer zweiten Reduktionsfolge wird die outermost reduction ihre Vorteile offen legen:
01 {leftmost innermost reduction}
02 fst(square 4,square 2)
03 = {definition of square}
04 fst(4 x 4, square 2)
05 = {definition of x}
06 fst(16, square 2)
07 = {definition of square}
08 fst(16, 2 x 2)
09 = {definition of x}
10 fst(16,4)
11 = {definition of fst}
12 16
|
01 {leftmost outermost reduction}
02 fst(square 4,square 2)
03 = {definition of fst}
04 square 4
05 = {definition of square}
06 4 x 4
07 = {definition of x}
08 16
09
10
11
12
|
Wir sehen hier die deutlichen Unterschiede in den Auswertungsstrategien. Für die Berechnung der Normalform sind mit der innermost reduction
fünf Schritte vonnöten, für die outermost reduction benötigen wir nur drei. Der Zusammenhang ergibt sich aus der Definition
von fst. fst gibt den ersten Wert eines Tupels zurück. Folgt man dieser Definition,
ist der zweite Wert dieses Tupels für die Berechnung nicht relevant. Da wir jedoch mit der innermost reduction immer den innersten Ausdruck
ersetzen, wird eine überflüssige Reduktion für square 2 durchgeführt. Die outermost reduction bietet einen weiteren
Vorteil, ein Aufruf wie fst(2,⊥) kann problemlos ausgewertet werden. Die innermost reduction terminiert bei der
Auswertung eines solchen Ausdrucks nicht.
Wir fassen zusammen:
- Outermost reduction terminiert häufiger als innermost reduction
- Wenn eine Reduktion terminiert liefern beide Strategien das gleiche Ergebnis
- Vorteil outermost reduction:
Wenn eine Normalform vorhanden ist, kann sie durch die outermost reduction berechnet werden
- Nachteil outermost reduction:
Gleiche Ausdrücke in Reduktionen müssen wiederholt berechnet werden. Lösung: Graphen.
Graphen
Bisher haben wir nur eine spezielle Form der Graphen kennengelernt: Bäume. Bäume wurden definiert als eine Menge von durch Kanten
miteinander verbundenen Knoten, wobei die Kanten gerichtet von der Wurzel zu den Blättern verlaufen. Zusätzlich durfte jeder Knoten
nur maximal einen Vorgängerknoten besitzen.
Bei Graphen entfallen diese Einschränkungen: ein Graph besteht aus Knoten, die durch Kanten verbunden sind.
Die Kanten können dabei entweder gerichtet oder ungerichtet sein.
Reduktion in Haskell
In Haskell werden spezielle Graphen eingeführt, die die sog. geteilten Ausdrücke ermöglichen.
Ein Beispiel:
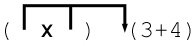
entspricht
(3+4) x (3+4). Jeder Pfeil stellt einen Zeiger auf eine einzelne Instanz des
Ausdrucks
(3+4) dar. Im ersten Beispiel der Reduktionsstrategien ändert sich nun die
Auswertung wie folgt:

Die geteilten Ausdrücke sind ebenfalls in lokalen Definitionen zu finden:
01 roots a b c = (((-b-d)/e, (-b+d)/e)
02 where d = sqrt(square b-4 x a x c)
03 e = 2 x a
|
Die erste Reduktion für
roots 1 5 3 ergibt:
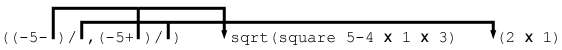
Mit dem Einsatz der Graphen wird der o.g. Nachteil in der outermost reduction beseitigt. Daraus folgt, dass die outermost reduction
keinerlei (jetzt bekannte) Nachteile beinhaltet und der innermost reduction überlegen ist.
Wir führen nun den Begriff der Lazy Evaluation ein:
Lazy Evaluation entspricht der leftmost outermost graph reduction. Sie ist das Standard-Reduktionsverfahren in Haskell.
Analog dazu können wir den Begriff der Eager Evaluation definieren:
Eager Evaluation entspricht der leftmost innermost graph reduction.
 Eine Folge der Lazy Evaluation ist, dass Ausdrücke in Haskell nicht strikt ausgewertet werden.
Eine Folge der Lazy Evaluation ist, dass Ausdrücke in Haskell nicht strikt ausgewertet werden.
Effizienz Lazy Evaluation
geg.: Eine Reduktionsfolge e1 -> e2 -> ... -> en, mit en in Normalform.
Der
Zeitbedarf für diese Reduktionsfolge beträgt
n + eps. Zusätzlich zur eigentlichen
Reduktion muss der Wert
eps addiert werden, um die Suche nach dem äußeren Ausdruck nicht zu vernachlässigen.
Wie gewichtig dieser Wert
eps ist, hängt von der Größe des Redex ab.
Der
Platzbedarf für eine Reduktion wird durch die Größe des größten Redex charakterisiert. Der Speicherplatz
kann durch die sog. "Garbage Collection" wiederholt genutzt werden.
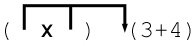

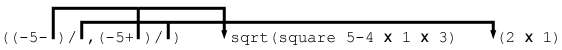
 Eine Folge der Lazy Evaluation ist, dass Ausdrücke in Haskell nicht strikt ausgewertet werden.
Eine Folge der Lazy Evaluation ist, dass Ausdrücke in Haskell nicht strikt ausgewertet werden.