Abschließend soll ein umfangreicheres Beispiel zur Verwendung von Bäumen präsentiert werden. Die nach David Huffman benannten Huffman-Bäume werden zur Komprimierung von Daten eingesetzt. Das Verfahren soll zunächst kurz beschrieben werden:
Die Idee, die hier zur Komprimierung von beispielsweise Texten verwendet wird, ist, den zu komprimierenden Text, der hier durch die Ascii-Kodierung repräsentiert wird, durch einen Code mit variabler Länge darzustellen.
Dazu ein Beispiel: Die Zeichenkette "text" wird in Ascii-Kodierung genau 4 Bytes, also 32 Bits belegen. Dies wäre, wenn nur diese Zeichenkette auftritt, gar nicht notwendig, da von den im Ascii-Zeichensatz vorhandenen Zeichen nur drei verwendet wurden, eins sogar doppelt. Um drei verschiedene Zeichen zu kodieren, genügten eigentlich zwei Bits (2^2 Möglichkeiten).
Nehmen wir an, folgende Kodierung würde verwendet werden:
Dann könnte die Zeichenkette "text" folgendermaßen dargestellt werden: 010110. Es wären nur noch 6 Bits statt 32 notwendig. Die gewählte Kodierung war allerdings nicht beliebig, wäre sie beispielsweise
dann käme die Bitfolge 01010 heraus, die allerdings auch bei der Kodierung von "tee" entstehen würde. Daher muß der gewählte Code eindeutig sein. Dies läßt sich dadurch erreichen, daß kein Code Präfix eines anderen ist. Diese Vorgabe und die Forderung nach einem minimalen Code, der eine optimale Komprimierung erreicht, lassen sich durch die Verwendung von Huffman-Bäumen erreichen.
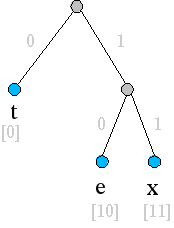
In einem Huffman-Baum sind die einzelnen Codes Blätter eines binären Baumes. Der Weg von der Wurzel zu den Blättern liefert den dazugehörigen Code. Wird auf dem Weg eine Verzweigung nach links genommen, wird zum Code eine binäre Null hinzugefügt, ansonsten ein binäre Eins. Der Huffman-Baum für die oben gezeigte korrekte Kodierung hat folgende Gestalt:

Für das gesamte Thema bietet sich eine Unterteilung in folgende Unterprobleme an:
Das Dekodieren ist am einfachsten zu implementieren. Anhand der Signatur läßt sich schon sehr gut die Aufgabe der Funktion ablesen. Sie erzeugt aus dem Huffman-Baum und der kodierten Bitfolge den Ursprungstext.
Die Funktionsweise ist recht offensichtlich. Anhand des ersten Zeichens der Bitliste wird entschieden, ob im Baum nach links oder rechts gegangen werden soll. Erreicht man ein Blatt, ist ein Zeichen dekodiert und wird in die Ergebnisliste aufgenommen; anschließend wird wieder an der Wurzel des Baumes mit dem Rest der Bitliste fortgefahren. Die Dekodierung ist beendet, wenn alle Bits abgearbeitet sind.
decode :: BTree Char -> [Bit] -> [Char]
decode t cs
= if null cs then [] else decode1 t cs
where decode1 (Leaf x) cs = x : decode t cs
decode1 (Fork xt yt) (L:cs) = decode1 xt cs
decode1 (Fork xt yt) (R:cs) = decode1 yt cs
Man könnte die Kodierfunktion am einfachsten implementieren, indem man den Ursprungstext durchläuft, das jeweilige Zeichen im Baum sucht und sich die Bitfolge von der Wurzel des Huffmanbaums zum Blatt merkt. Allerdings wäre dies reichlich ineffizient, da auch bei wiederkehrenden Buchstaben stets die gleiche Suche durchgeführt werden müßte und die Suche in normalen Bäume an sich schon recht ineffizient ist.
Aus diesem Grund wird der Baum zunächst in eine Codetabelle umgewandelt, in der dann besser nach Buchstaben gesucht werden kann.
type CodeTable = [(Char,[Bit])]encode :: BTree Char -> [Char] -> [Bit] encode t = concat . map (codelookup codetable) where codetable = transform t
codelookup :: CodeTable -> Char -> [Bit] codelookup ((x,bs) : xbs) y = if x == y then bs else codelookup xbs y
transform :: BTree Char -> CodeTable transform (Leaf x) = [(x,[])] transform (Fork xt yt) = hufmerge (transform xt) (transform yt)
hufmerge :: CodeTable -> CodeTable -> CodeTable hufmerge [] ycs = [(y,R: cs) | (y,cs) <- ycs] hufmerge xbs [] = [(x,L: bs) | (x,bs) <- xbs] hufmerge ((x,bs):xbs) ((y,cs):ycs) | length bs <= length cs = (x,L:bs) : (hufmerge xbs ((y,cs):ycs)) | otherwise = (y,R:cs) : hufmerge ((x,bs):xbs) ycs
Jeder Buchstabe wird in der Codetabelle nachgeschlagen, die einzelnen Ergebnislisten (die Bitfolgen aller Buchstaben) werden anschließend konkateniert.
Wie bereits gezeigt, ist die Kodierung der einzelnen Buchstaben abhängig von der Häufigkeit, mit der sie auftreten. Daher ist ein Teilproblem, diese Häufigkeiten zu berechnen.
Die Funktion sample bekommt als Parameter den zu untersuchenden Text und liefert eine Liste aus Buchstaben-Häufigkeiten-Tupeln zurück.
Die Idee dabei ist, im ersten Schritt den Ursprungstext nach den Buchstabenwertigkeiten zu sortieren. Beispielsweise würde aus dem Text "text" die Zeichenfolge "ettx". Anschließend werden gleiche Folgen zusammengefaßt. Dies übernimmt die Funktion collate. Abschließend werden die Tupel nach der Auftrittshäufigkeit aufsteigend sortiert.
sample :: [Char] -> [(Char,Int)] sample = sortby freq . collate . sortby idcollate :: [Char] -> SampleList collate [] = [] collate (x:xs) = (x,1+(length ys)):collate zs where (ys,zs) = span (==x) xs
Abschließend soll noch der wohl interessanteste Teil besprochen werden: die Erzeugung der Huffman-Bäume. Zunächst als Überblick die Signatur der Funktion. Wie man sieht, erhält sie als einzigen Parameter die Liste, die die Funktion sample liefert. Daraus wird ein HuffTree erzeugt. Diese ist ein erweiterter binärer Baumtyp, der zur Steigerung der Effizienz um zusätzliche Attribute erweitert wurde, ansonstens aber mit den von encode und decode erwarteten binäre Bäumen übereinstimmt.
mkHuff :: [(Char,Int)] -> HuffTree
data HuffTree = Tip Int Char
| Node Int HuffTree HuffTree
deriving(Show)Der Algorithmus läuft wie folgt ab:
Für das in diesem Kapitel beschriebene Beispiel wäre der Ablauf folgender:

Abschließend noch die Implementierung der Funktion mkHuff:
mkHuff :: [(Char,Int)] -> HuffTree mkHuff = unwrap . until singleton combine . map mktip
Der gesamte Code befindet sich mit den anderen Beispielen im Anhang.
