Die zweite Klasse der binären Bäume sind die sogenannten Suchbäume (auch "labelled binary trees" genannt). Wie der Name bereits andeutet, sind sie besonders dafür geeignet, dass man in ihnen sucht. Aufgrund dieser Eigenschaft, bieten sie sich auch dafür an, Mengen zu repräsentieren. Der Test, ob ein Element in einer Menge vorhanden ist, wird sehr häufig benutzt und ist letztendlich nichts anderes als eine Suche.
Die Eigenschaften binärer Suchbäume ähneln denen der normalen binären Bäume, sind allerdings an den etwas anderen Aufbau angepaßt.
Eine weitere Eigenschaft ist, dass die Liste, die beim Glätten eines Suchbaumes entsteht, stets sortiert ist, dies wird an einer späteren Stelle noch ausgenutzt.
Binäre Suchbäume haben einen etwas anderen Aufbau als die bisher besprochenen Baumtypen. Die Informationen befinden sich nicht in speziellen Blattknoten, sie stecken in den Verzweigungen. Außerdem gibt es spezielle Markierungen für leere Bäume. Sie sind in Haskell bespielsweise folgendermaßen definiert:
data (Ord a) => Stree a = Null
| Fork (Stree a) a (Stree a)Die in einem Suchbaum speicherbaren Elementen unterliegen einer Einschränkung: auf ihnen muß eine Ordnungsrelation definiert sein. Dies wird durch eine Einschränkung des Kontextes auf Typen der Typklasse Ord erreicht. Semantisch wird festgelegt, dass alle Elemente, die kleiner als das am Knoten gespeicherte Element im linken Teilbaum liegen, die größeren im rechten.
Einen Baum aus einer Liste erzeugen
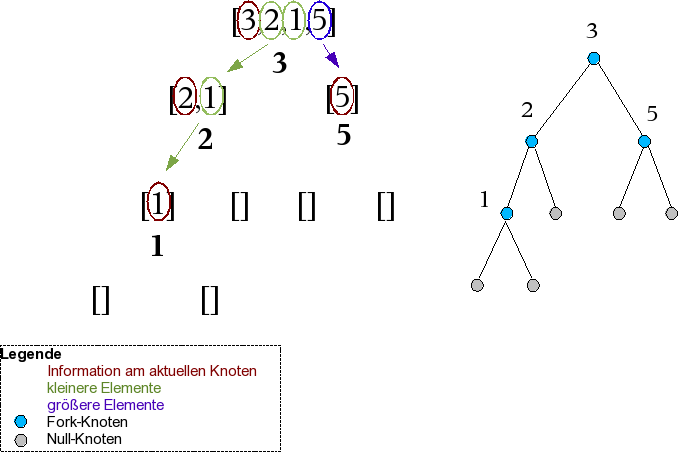
Die Vorgehensweise, einen binären Suchbaum zu erstellen, unterscheidet sich nicht sehr von der, einen einfachen binären Baum aufzubauen. Zunächst wird immer das erste Element der Liste genommen und als Information für den aktuellen Knoten benutzt. Die Restliste wird nun nicht einfach in zwei Teile geteilt, wie dies im vorherigen Kapitel der Fall war. Vielmehr wird der Rest aufgeteilt in eine Teilliste, deren Elemente kleiner sind als das des aktuellen Knotens, und eine, deren Elemente größer sind. Aus diesen Listen erzeugte Bäume werden die linken und rechten Unterbäume. Die eben beschriebene Verarbeitung findet dort ebenso statt. Leere Bäume werden erzeugt, wenn leere Listen verarbeitet werden. Eine Graphik soll dieses Verfahren illustrieren.

Umgesetzt in Haskell sieht dies so aus:
mkStree :: (Ord a) => [a] -> Stree a
mkStree [] = Null
mkStree (x:xs) = Fork (mkStree smaller) x (mkStree larger)
where (smaller,larger) = partition (<= x) xs
partition :: (a->Bool) -> [a] -> ([a],[a])
partition p xs = ([ x | x <- xs, p x],
[ y | y <- xs, (not . p) y])
Hier wird über Pattern Matching bestimmt, welcher Fall anzuwenden ist. Ist die Liste leer, wird einfach ein leerer Baum erzeugt. Ansonsten wird das erste Element der Liste genommen und zwei Listen, smaller und larger, berechnet, die die eben beschriebenen Eigenschaften besitzen.
Die Berechnung wird durch eine Funktion partition erledigt. Diese erhält als Parameter ein Prädikat und eine Liste. Als Rückgabewert liefert sie ein Tupel zwei Listen; die eine Liste enthält Elemente der Ursprungsliste, für die das Prädikat gilt, die zweite die restlichen Elemente. Die Listen wird einfach durch List comprehension erzeugt.
Sortieren mit Suchbäumen
Wie bereits in der Einleitung zu den Suchbäumen erwähnt, gilt folgendes: Die Liste, die durch Glätten eines Suchbaums entsteht, ist stets sortiert. Da ja bereits über mkStree die Möglichkeit besteht, aus einer Liste einen Suchbaum zu erzeugen, läßt sich über diese Transformation eine Liste sortieren.
Eine einfache Sortierungsfunktion könnte also so aussehen:
sort :: (Ord a) => [a] -> [a] sort = flatten . mkStree
Wenn man diese beiden komponierten Funktionen zusammenfasst und den Zwischenbaum entfernt, ergibt sich daraus eine Implementierung von Quicksort.
Elementtest auf binären Suchbäumen
Binäre Suchbäume lassen sich sehr gut zum Repräsentieren von Mengen einsetzen. Eine der wichtigsten Operationen ist der Test, ob ein Element in einer Menge vorhanden ist. Dieser läßt sich recht einfach implementieren.
member :: (Ord a) => a -> Stree a -> Bool member x Null = False member x (Fork xt y yt) | x < y = member x xt | x == y = True | x > y = member x yt
Interessant ist hier das Verhalten an den Fork-Knoten: Entspricht das hier gespeicherte dem gesuchten Element, wird True zurückgeliefert, ansonsten wird abhängig vom Größenvergleich entweder im linken oder rechten Teilbaum gesucht. Hier wird die aufgebaute Ordnung des Baumes ausgenutzt und somit das Verfahren recht effizient.
Löschen und Einfügen in binäre Suchbäume
Neben dem Test, ob Elemente in einer Menge vorhanden sind, sind das Einfügen und Löschen die wichtigsten Operation auf Mengen.
Das Einfügen ist am einfachsten. Soll in einen leeren Baum eingefügt werden, entsteht ein neuer Fork-Knoten mit zwei leeren Unterbäumen. Anderenfalls wird entschieden, ob das neue Element in den linken oder in den rechten Unterbaum einsortiert wird. Es entsteht an dieser Stelle ein neuer Knoten, der jeweilige Unterbaum wird dann neu berechnet. Zusammengefaßt läßt sich sagen, daß beim Einfügen alle Knoten oberhalb des eingefügten Knotens verändert werden.
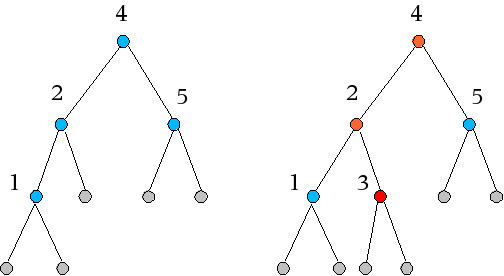
Der linke Baum zeigt die Ausgangssituation, der rechte nach dem Einfügen der "3". Rot ist der neu eingefügte Knoten (dort befand sich ja vorher ein leerer Unterbaum), orange sind die veränderten Knoten.
Der Code sieht wie folgt aus:
insert :: (Ord a) => a -> Stree a -> Stree a insert x Null = Fork Null x Null insert x (Fork xt y yt) | (x < y) = Fork (insert x xt) y yt | (x == y) = Fork xt y yt | (x > y) = Fork xt y (insert x yt)
Das Löschen aus einem Baum ist ein wenig komplizierter und soll nur grundsätzlich beschrieben werden. Grundsätzlich entspricht das Verfahren dem Einfügen, das einzige Problem liegt darin, ein nicht-Blattknoten zu löschen. Soll dies geschehen, muß der Baum so neu organisiert werden, dass die semantischen Vergaben erfüllt bleiben.
Dies kann folgendermaßen realisiert werden.
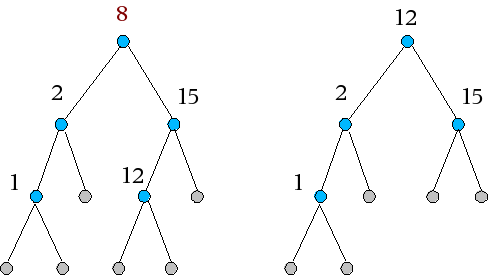
Im linken Baum soll die 8 entfernt werden. Der Trick ist, aus dem rechten Teilbaum das kleinste Element zu finden und an die Stelle des gelöschten Elements zu setzen, wie dies hier mit der 12 geschehen ist.
delete :: (Ord a) => a -> Stree a -> Stree a delete x Null = Null delete x (Fork xt y yt) | (x < y) = Fork (delete x xt) y yt | (x == y) = join xt yt | (x > y) = Fork xt y (delete x yt)join :: (Ord a) => Stree a -> Stree a -> Stree a join xt yt = if empty yt then xt else Fork xt (headTree yt) (tailTree yt)
empty :: (Ord a) => Stree a -> Bool empty Null = True empty (Fork xt y yt) = False
splitTree :: (Ord a) => Stree a -> (a,Stree a) splitTree (Fork xt y yt) = if empty xt then (y,yt) else (x, Fork wt y yt) where (x,wt) = splitTree xt
headTree :: (Ord a) => Stree a -> a headTree = fst . splitTree
tailTree :: (Ord a) => Stree a -> Stree a tailTree = snd . splitTree
