Grundlegende Konzepte
... [Seminar
"Haskell"] ... [Inhaltsübersicht]
... [zurück] ... [weiter] ...
Definitionen
Wie in den meisten Programmiersprachen gibt es auch in Haskell ein if-then-else-Konstrukt. Abhängig von der Auswertung der Bedingung wird entweder der then-Ausdruck oder der else-Ausdruck ausgewertet.
Beispiel:
smaller :: (Integer, Integer) -> Integer
smaller (x,y) = if x < y then x else y
Sowohl der then-Teil als auch der else-Teil müssen zwingend vorhanden sein.
Schachtelungen sind möglich.
Beispiel:
signum :: Integer -> Integer
signum x = if x < 0 then -1 else
if x == 0 then 0 else 1
Wenn in Anwendungsfällen viele elementare Fälle abgeprüft werden sollen (z.B. Tastaturabfrage), können if-then-else-Verschachtelungen beliebig kompliziert werden. Um den Code in diesen Fällen komfortabler und lesbarer gestalten zu können, unterstützt Haskell auch case-Konstrukte.
Beispiel:
f :: Char -> Integer
f x = case x of
'a' -> 1
'b' -> 23
'c' -> 42
_ -> -1
Die im Case-Verteiler aufgeführten Fälle werden nacheinander abgeprüft. Der Unterstrich steht für alle Werte von x, die mit keinem der anderen bis hierher abgearbeiteten Fälle übereinstimmen. Der Unterstrich ist sozusagen der else-Fall des Case-Konstruktes. Die einzig sinnvolle Positionierung des Unterstriches ist in der letzten Zeile des Case-Verteilers, da nach dem Unterstrich aufgeführte Fälle nie abgeprüft werden.
Ist in einem Case-Verteiler kein solcher else-Fall definiert, führt jede Auswertung des Case-Konstruktes mit einem nicht auf einen der definierten Fälle passenden Wert zu einem Laufzeitfehler.
Als Alternative zum Case-Verteiler können Funktionen in Haskell auch stückweise, also in Abhängigkeit von Argumentwerten, definiert werden.
Die obige Funktion f könnte dementsprechend wie folgt definiert werden:
f 'a' = 1
f 'b' = 23
f 'c' = 42
f _ = -1
Auch hier steht der Unterstrich wieder für alle bis hierher noch nicht abgeprüften Fälle. Die Reihenfolge der Definitionen ist wie beim Case-Konstrukt relevant. Nach dem Unterstrich definierte Fälle werden niemals abgeprüft. Ohne Definition des Unterstriches führt jede Auswertung der Funktion f mit einem auf keinen der definierten Fälle passenden Argument zu einem Laufzeitfehler.
Case-Verteiler sind eine gute Alternative zu geschachtelten if-then-else-Konstrukten, wenn es um das Abprüfen mehrerer elementarer Fälle geht. Soll ein Ausdruck jedoch in Abhängigkeit von einer Sequenz von booleschen Bedingungen ausgewertet werden, erschöpfen sich die Möglichkeiten eines Case-Verteilers.
Ein Beispiel ist die Signum-Funktion:
signum :: Integer -> Integer
signum x = if x < 0 then -1 else
if x == 0 then 0 else 1
Noch deutlicher wird die Nichtanwendbarkeit eines Case-Verteilers zur Vermeidung solcher if-then-else-Schachtelungen mit booleschen Bedingungen beim Vergleich zweier Argumente:
compare :: Integer -> (Integer -> Integer)
compare x y = if x < y then -1 else
if x > y then 1 else 0
Eine solche Sequenz von booleschen Bedingungen kann komfortabel mit sogenannten Guards (Guarded Equations) definiert werden.
Die Definition der Signum-Funktion unter Verwendung von Guards:
signum :: Integer -> Integer
signum x
| x < 0 = -1
| x == 0 = 0
| x > 0 = 1
Der Vergleich zweier Argumente unter Verwendung von Guards:
compare :: Integer -> (Integer -> Integer)
compare x y
| x < y = -1
| x > y = 1
| x == y = 0
Jeder einzelne Fall wird mit | eingeleitet und besteht aus einer booleschen Bedingung (dem "Guard") und einem Ausdruck, der ausgewertet wird, sofern die zugehörige Bedingung zutrifft. Bedingung und Ausdruck sind durch ein Gleichheitszeichen voneinander getrennt. Sollten mehrere Bedingungen zutreffen, so wird der Ausdruck der zuerst aufgeführten Bedingung ausgewertet.
Die Funktionsdefinitionen mit Hilfe von Guards sind lesbarer und verständlicher als diejenigen mit geschachtelten if-then-else-Konstrukten, da alle Fälle mit ihren Konsequenzen explizit aufgelistet werden.
Auch für Guarded Equations ist ein (letzter) Fall vorsehbar, dessen Ausdruck immer dann ausgewertet wird, wenn keine der vorigen Bedingungen zu TRUE ausgewertet wurde:
compare :: Integer -> (Integer -> Integer)
compare x y
| x < y = -1
| x > y = 1
| otherwise = 0
otherwise wertet stets zu TRUE aus. Daher wirkt der zugeordnete Ausdruck wie ein else-Fall.
Bei der Durchführung mathematischer Berechnungen kommt es häufig vor, dass das Ergebnis einer Teilberechnung an mehreren Stellen einer Funktion benötigt wird. Eim simples Beipiel ist die folgende Funktion:
f(x,y) = (a+1)*(a+2) ; wobei a = (x+y)/2
Mit einer fast identischen Notation lässt sich das a in Haskell lokal definieren:
f :: (Float,Float) -> Float
f (x,y) = (a+1)*(a+2) where a = (x+y)/2
Die lokale Definition folgt direkt im Anschluss an die Funktionsdefinition und wird durch das Schlüsselwort where eingeleitet. Es sind auch mehrere lokale Definitionen möglich:
f :: (Float,Float) -> Float
f (x,y) = (a+1)*(b+2)
where a = (x+y)/2
b = (x+y)/3
Der Sichtbarkeitsbereich einer lokalen Definition ist beschränkt auf die rechte Seite des Gleichheitszeichens der Funktionsdefinition. Das bedeutet zum einen, dass auf diese Definitionen ausserhalb der jeweiligen Funktionsdefinition nicht zugegriffen werden kann, zum anderen überdecken die lokalen Definitionen in diesem Bereich alle anderen eventuell existierenden gleichnamigen Definitionen.
Werden in der Funktionsdefinition Guards verwendet, so erstreckt sich der Sichtbarkeitsbereich einer lokalen Definition auf alle aufgelisteten Fälle:
f :: Integer -> Integer -> Integer
f x y
| x < 11 = x + a
| x > 10 = x - a
where a = square(y+1)
Eine Alternative zur lokalen Definition mit where ist das let-in-Konstrukt. Mit let-in formulierte lokale Definitionen haben den selben Effekt wie where-Definitionen, nur werden sie vor der eigentlichen Funktionsdefinition notiert:
f :: (Float,Float) -> Float
f (x,y) =
let a = (x+y)/2
b = (x+y)/3
in (a+1)*(b+2)
Die Entscheidung für die Verwendung von where oder let in ist meistens von den persönlichen Präferenzen des jeweiligen Programmierers geprägt. Möglich, wenn auch aus Gründen der Lesbarkeit nicht ratsam, sind sogar Funktionsdefinitionen mit beiden Arten von lokalen Definitionen.
Beispiel:
f :: Integer -> Integer
f x =
let a = x + 1
in a*b
where b = x - 1
Theoretisch denkbar, praktisch allerdings ohne Sinn, ist auch der folgende Fall:
f :: Integer -> Integer
f x =
let y = x + 1
in y
where y = x - 1
In diesem Fall würden die mit let getätigten Definitionen die where-Definitionen überdecken und damit überflüssig machen.
Rekursive Funktionen haben in der funktionalen Programmierung eine wesentlich grössere Bedeutung als in imperativen Programmiersprachen. In letzteren überwiegt die Nutzung von Schleifen, selbst bei Problemstellungen, für die einfache und elegante rekursive Lösungen naheliegend wären. Die Rekursion verdankt ihre Bedeutung in der funktionalen Programmierung wohl nicht zuletzt auch der Tatsache, dass Schleifen hier nicht einsetzbar sind. Weil der Wert eines Bezeichners im Programmablauf nicht verändert werden kann, fällt die Formulierung von Schleifen in Ermangelung von Schleifenzählern oder Abbruchkriterien schwer.
Ein gutes Beispiel für Rekursion ist die Fakultät:
factorial :: Integer -> Integer
factorial n = if n==0 then 1 else n * factorial(n-1)
Auch diese Definition kann stückweise formuliert werden:
factorial :: Integer -> Integer
factorial 0 = 1
factorial n = n * factorial (n-1)
Die rekursive Funktion factorial arbeitet hervorragend für positive Zahlen. Wird factorial jedoch mit einem negativen Argument aufgerufen, so terminieren die Berechnungen nie. Für negative Zahlen ist die Fakultät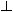 
. Um für den Fall eines negativen Argumentes statt einer Endlos-Rekursion eine aussagekräftige Fehlermeldung zu erhalten, wird die vordefinierte Funktion error verwendet. Sie nimmt als Argument eine Fehlermeldung als String entgegen, die sie, sobald sie ausgewertet wird, ausgibt. Zusätzlich beendet sie sofort jegliche Auswertungen.
Die angepasste Funktion factorial:
factorial :: Integer -> Integer
factorial n =
| n < 0 = error "negative argument"
| n==0 = 1
| n > 0 = n * factorial(n-1)
... [Seminar
"Haskell"] ... [Inhaltsübersicht]
... [zurück] ... [weiter] ...
