Ausdrücke werden durch schrittweise Substitution, Vereinfachung und Rechnen ausgewertet. Hierbei werden Ersetzungsregeln verwendet, deren linke Seiten im Zuge der Auswertung eines Ausdrucks durch die rechten Seiten ersetzt werden. Abgesehen von einigen eingebauten einfachen Operationen werden die Ersetzungsregeln vom Programmierer in Form von Funktionsdefinitionen vorgegeben. Jeder Ausdruck wird auf sein einfachstes Äquivalent reduziert. Wenn ein Ausdruck nicht mehr weiter reduziert werden kann, wird dies als Normalform bezeichnet.
Eine Reduktionssequenz für einen Beispielausdruck:
square (3 + 4)
Auswertung der Additionsquare 7Auswertung von 'square'7 * 7Auswertung der Multiplikation49
Im ersten und dritten Reduktionsschritt werden die integrierten Regeln für Addition und Multiplikation verwendet. Im zweiten Schritt findet die vom Programmierer aufgestellte Ersetzungsregel 'square x = x * x' Anwendung. '49' kann schliesslich nicht mehr weiter reduziert werden, befindet sich also in Normalform.
In den meisten Fällen existiert mehr als eine Reduktionssequenz, um einen Ausdruck zu vereinfachen. So könnte die Auswertung von square (3 + 4) im ersten Schritt auch mit der Anwendung der vom Programmierer aufgestellten Ersetzungsregel square x = x * x begonnen werden. Alle existierenden Möglichkeiten der Reduktion führen jedoch (sofern sie terminieren) zum selben Ergebnis.
Dass die Voraussetzung des Terminierens keine Selbstverständlichkeit ist, zeigt folgendes Beispiel:
three :: Integer -> Integer
three x = 3
infinity :: Integer
infinity = infinity + 1
Das Ergebnis der Funktion three ist der Integer-Wert 3, unabhängig von dem Integer-Argument x. Nicht ganz so klar ist, welcher Integer-Wert das Ergebnis der Funktion infinity sein soll. Als Ersetzungsregel jedoch ist infinity problemlos anwendbar.
Für die Auswertung des Ausdruckes three infinity ergeben sich zwei mögliche Reduktionssequenzen. Wird mit der Auswertung von three begonnen, so terminiert die Reduktion schon nach dem ersten Schritt:
three infinityAuswertung von 'three'3
infinity begonnen, so ergibt sich eine nicht terminierende Reduktionssequenz:
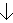
three infinityAuswertung von 'infinity'three (infinity + 1)Auswertung von 'infinity'three ((infinity + 1) + 1).
.
.
Die Aufgabe des Compilers besteht folglich darin, für die Auswertung eines Ausdruckes aus allen möglichen Reduktionssequenzen eine terminierende und dazu noch möglichst effiziente auszuwählen. In Haskell geschieht dies mittels einer 'lazy evaluation' genannten Reduktionsstrategie, die im weiteren Verlauf dieses Seminares noch ausführlich dargestellt werden wird.
In der funktionalen Programmierung sind sämtliche Ausdrücke nichts anderes als Denotationen von Werten. Selbst jeder Ausdruck in Normalform ist lediglich eine Repräsentation eines Wertes, so auch z. B. 49.
Die Unterscheidung zwischen (abstrakten) Werten und ihren Repräsentationen ist grundlegend. So lassen sich für den durch den Ausdruck 49 beschriebenen Wert noch andere Repräsentationen finden: z.B. 49.0, XLIX oder 110001.
Wenn der einzige Zweck von Ausdrücken in der funktionalen Programmierung in der Denotation von Werten besteht, macht es Sinn zu fordern, dass tatsächlich jeder (syntaktisch korrekte) Ausdruck einen Wert denotiert.
Dem entgegen stehen Ausdrücke wie infinity (Definition siehe oben) oder Divisionen durch Null.
Die Lösung besteht in der Einführung eines zusätzlichen Symbols: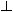 
("Bottom") steht für den undefinierten Wert eines bestimmten Typs. So denotiert infinity einen undefinierten Wert 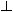vom Typ Integer, während z.B. 1/0 einen undefinierten Wert 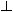vom Typ Float beschreibt.
Durch die Einführung von 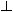gilt: Jeder (syntaktisch korrekte) Ausdruck denotiert einen Wert.
Die Gesamtheit aller Funktionen lässt sich bezüglich der Behandlung des undefinierten Wertes 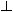als Argument in strikte und nicht-strikte Funktionen einteilen. Eine strikte Funktion bildet 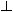stets auf 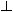ab. three ist ein Beipiel für eine nicht strikte Funktion, da der undefinierte Wert 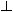auf 3 abgebildet wird.
So wichtig 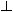für das theoretische Konzept der funktionalen Programmierung auch ist, der Rechner wird dieses Symbol nicht zurückgeben, wenn er mit der Auswertung eines Ausdrucks beschäftigt ist, dessen Wert 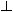ist. Er wird entweder eine Fehlermeldung ausgeben (z.B. im Fall einer Division durch Null) oder in endloser Regungslosigkeit verharren (z.B. bei der Auswertung von infinity).
