Von
Oliver R. Ahlemann
Mi7672
Meine Ausführungen beziehen sich ausschließlich auf das Bearbeiten von Sampling Dateien. Ich grenze Echtzeitbearbeitung einfach mal aus. Das Prinzip ist ja auch bei Echtzeitbearbeitung das gleiche. Wenn man sich vorstellt, dass ein Filter nicht nur auf Softwareebene realisiert sein kann sonder auch fest verdrahtet sein kann.
Hierzu brauche ich wohl nicht vier zu erzählen. Bestimmte Bereiche eines Samples können also auf diese Weise bearbeitet werden. Die einzige Problematik bei diesen Bearbeitungen, sind die Schnittstellen. Es kann dabei zu Knackgeräuschen kommen, wenn eine Unstetigkeit auftritt. Hierzu führen viele Anwenderprogramme eine Interpolation der benachbarten Werte durch, um so das Störgeräusch zu unterbinden.
Durch diese Funktionen kann der Pegel des Audiosignals bestimmt werden. Hierbei werden immer alle Werte des Signals in gleichem Maße verändert. Als Verstärkung wird allgemein die Pegelveränderung bezeichnet, also dessen Anhebung , als Dämpfung wird die Absenkung des Pegels bezeichnet. Als Normalisierung bezeichnet man eine maximale Verstärkung des Signals. Durch eine vorherige Analyse wird der Zeitpunkt mit dem höchsten Pegel (Peak) bestimmt. Nun wird das Signal derart verstärkt, dass der Peak die obere Aussteuerungsgrenze (0 db) erreicht.
Die Mischung von Audiodateien kann durch die Addition der einzelnen Samplewerte erreicht werden. In der Praxis ist bei der Addition von Signalen anschließend eine Normalisierung nötig, da man sonst Signale erhalten kann, welche zu Laut sind und somit störend wirken.
Durch Fades sind gleichmäßige Ein- und Ausblendungen des Signals möglich. Man verwendet je nach Einsatzzweck lineare oder logarithmische Fades. Für Überblendungen (Crossfades) werden Fades mit einem logarithmischen Verlauf verwendet, da dadurch die empfundene Lautstärke des Summensignals weitgehend gleich bleibt.
Es gibt 2 unterschiedliche Arten von Filtern.
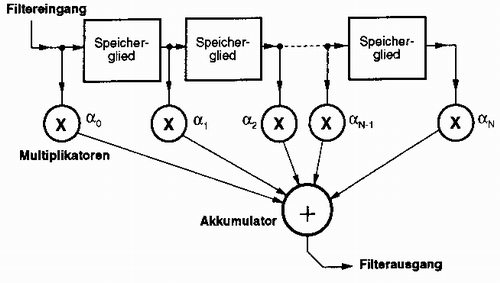
Der schematische Aufbau der beiden verschieden Filtertypen ist in den Abbildungen zu sehen. Die Audiodaten werden in der Kette der Speicherglieder mit jedem Taktzyklus weitergeschoben. Die Ausgangswerte gelangen auf einen Multiplikationskomplex. Von da aus werden die Daten mit jedem Takt auf einen Akkumulator geschoben, also aufsummiert. Das Ergebnis des Akkus entspricht dem Filterausgangswert.

Abbildung 16: FIR (Finite Impules Response)
FIR- FORMEL
YN = a0XN + a1XN-1 + .... + aN-1X1 + aNX0
N Ordnung des Filters
Die Filterkoeffizienten a sind fest. Für jede Filterfunktion sind diese vorgegeben, sie hängen von Filtertyp ab. Je nach der Dimensionierung ergeben sich verschiedene Filter mit Tiefpass-, Hochpass-, Bandpass-, Bandsperrcharakteristik. Die Filterordnung, also der Anzahl der Stufen, ist ebenfalls für die Koeffizienten wichtig. Eine besondere Eigenschaft von FIR Filtern ist, dass die Durchlaufzeit konstant ist. Man kann die Durchlaufzeit folgendermaßen berechnen:
T = N / Fa
Fa Abtastfrequenz
Es gibt wie erwähnt noch eine zweite Klasse von Filtern, die IIRs. Theoretisch haben diese eine unendlich lange Impusantwort. Es ergeben sich ausserdem folgende Unterscheidungsmerkmale:
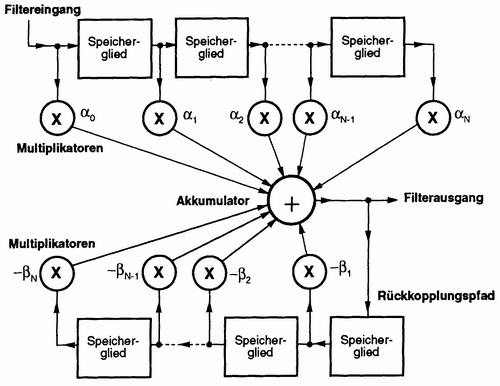
Abbildung 17: IIR (Infinite Impulse Response)
IIR-Formel
YN = a0XN + a1XN-1 + .... + aN-1X1 + aNX0 -b0YN - b1YN-1 - .... - bN-1Y1 - bNY0
Wie man sieht, handelt es sich um rekursive Vorgänge, die sich ergebenen Ausgangswerte gehen in die neuen Berechnungen wieder ein. IIR Filter setzten zusätzlich einen Rückkopplungspfad ein. Man gewinnt den Eindruck, dass ein Mehraufwand nötig ist, doch in der Regel kommen IIR-Filter mit wenigern Stufen aus als FIR- Filter. Durch eine geeignete Einstellung der Kooffizienten, kann man eigentlich alle Filterungen erreichen.
Filter bieten die Möglichkeit, den Frequenzgang bzw. die Klangfarbe von Audiomaterial zu beeinflussen. Technische Gründe für eine Frequenzgangkorrektur sind beispielsweise das Vorhandensein tieffrequenten Störschalls (z.B. Trittschall), starkes Rauschen (z.B. bei alten Magnetbändern oder zu gering ausgesteuerten Aufnahmen), verursacht durch ungünstige Aufnahmebedingungen. Beim künstlerisch-ästhetischen Einsatz kann durch Filter die Klangfarbe beeinflußt werden.
Komfortable Filter bieten folgende Parameteränderungen:
Es werden nur hohe bzw. tiefe Frequenzen durchgelassen
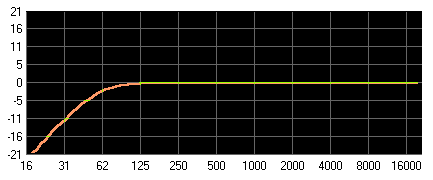
Abbildung 18: Hochpass
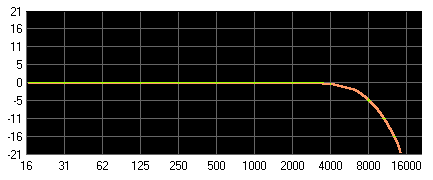
Abbildung 19: Tiefpass
Hierbei werden nur bestimmte Frequenzen durchgelassen, je nachdem wie der Filter eingestellt wurde
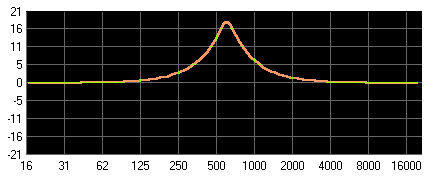
Abbildung 20: Bandpass
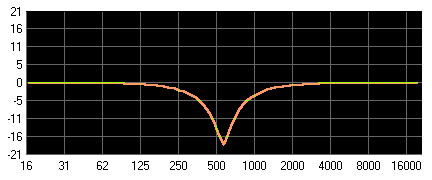
Abbildung 21: Bandstop
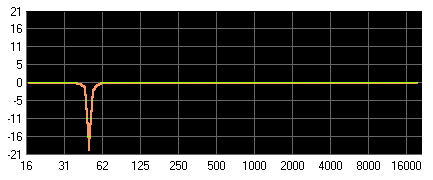
Abbildung 22: Lochfilter, schmale Bandsperre
Pegelerhöhung von tiefen bzw. hohen Frequenzen
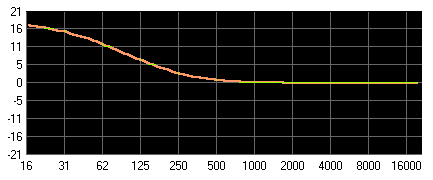
Abbildung 23: Tiefenanhebung
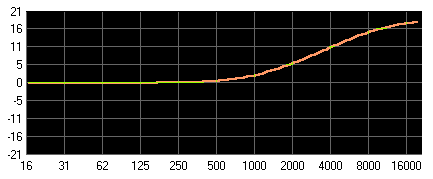
Abbildung 24: Höhenanhebung
Wie man sieht, können die einzelnen Filtercharakteristika auch miteinander kombiniert werden.
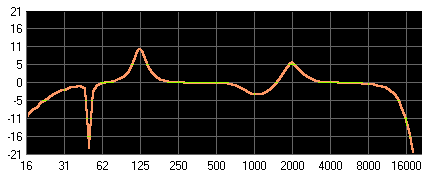
Abbildung 25: Kombination aus High-pass, Notch-filter, Band-pass, Band-reject, Band-pass und Low-pass
Die letzte Abbildung zeigt anhand einiger Frequenzverläufe die Filterung von einer Audiodatei mit einigen der eben angesprochenen FIR-Filter:
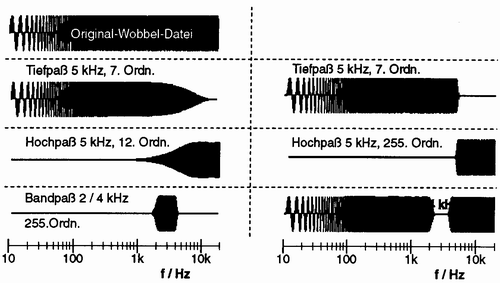
Abbildung 26: Beispielfilterungen
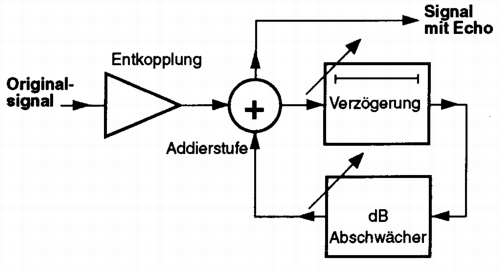
Abbildung 27: Prinzip der künstlichen Echoerzeugung
Bei der Erzeugung eines Echos, wird das Originalsignal verzögert und anschießend wird das verzögerte Signal dem Original wieder beigemischt. Hierbei sind 2 Parameter von entscheidender Bedeutung:
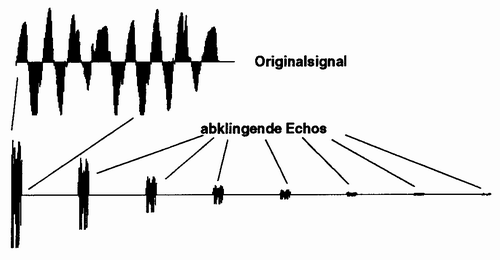
Abbildung 28: Erzeugung abklingender Echos bei einem Echopegel von 50% (-6 dB)
Der Abschwächer kann auch als Verstärker wirken. Damit kann man durch die Rückkopplung eine Aufschaukelung des Signals bewirken, bis es zur Begrenzung kommt. Es gibt auch Sondereffekte, wie zum Beispiel das Einmalecho.
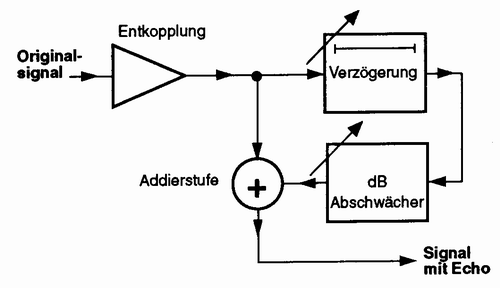
Abbildung 29: Erzeugung von einem Einmal-Echo
Phaser und Flanger ähneln in ihrem Aufbau stark einem Einmal Echo. Der Unterschied ist jedoch, dass die Phase bzw. Verzögerung über einen Steuergenerator langsam verändert wird. Die maximalen Verzögerungszeiten betragen hier ca. 100 ms Beim Phasing wird das Signal in seiner Phase verschoben und dem Originalsignal wieder zugemischt. Beim Flanging handelt es sich um eine Verzögerung. Flanging erzeugt mehrere Nullstellen im Frequenzgang als Phasing.
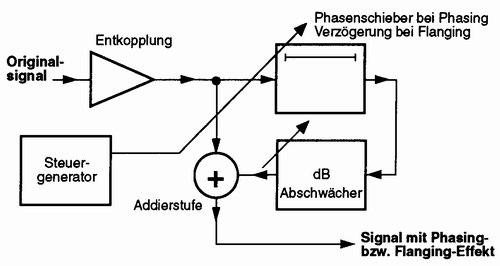
Abbildung 30: Schematische Arbeitsweise des Phasing bzw. Flanging
Hier sieht man die angesprochenen Nullstellen im Frequenzgang. Oft wird hierbei von einem Kammeffekt gesprochen. Werden Geräusche mit einem reichen Spektrum so bearbeitet, wie zum Beispiel ein Orchester oder eine Orgel, dann hat man den Eindruck, die Musik würde an einem vorbeifliegen und sich in die Lüfte erheben.

Abbildung 31: Wirkungen des Flanging im Frequenzbereich. a unverändertes Wobblesignal, b Flanging mit einer momentanen Verzögerungszeit von 10 ms, c bei 20 ms, d bei 40 ms
Ziel ist es, einen volleren Klangeindruck zu schaffen. Der Choruseffekt entseht durch die Beimischung des verzögerten Signals, wobei die Verzögerungszeiten zwischen 10 und 30 ms liegen. Dabei entstehen Kammfiltereffekte: bestimmte Frequenzbänder des Orginals werden ausgelöscht, andere hervorgehoben. Die Verzögerungszeit wird von einer Sinusschwingung moduliert, um nicht-statische Phasenverschiebungen (modulierte Kammfiltereffekte) zu erreichen.
Hall zu erzeugen, gehört zu den etwas aufwendigeren Effekten. Theoretisch entsteht Hall durch die Generierung von unendlich vielen Echos mit unendlich vielen verschiedenen Laufzeiten. Nach der Erstverzögerung, die das primäre Hallsignal erzeugt, folgen zu unregelmäßigen Zeitpunkte andere Echos. Das Problem bei der Hallerzeugung ist, dass man Reflektionspunkte simulieren muss. Der Rechenaufwand steigt mit der Anzahl dieser Reflexionspunkte. Gute Algorithmen sind sehr rechenintensiv, da sie die statistische Verteilung der Reflexionen im Raum simulieren müssen.
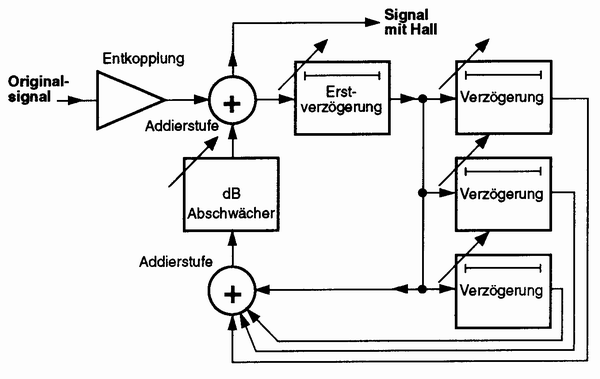
Abbildung 32: Prinzip der künstlichen Hallerzeugung
Hierbei wird das Signal gedehnt oder gestaucht., wobei sich die Abspielgeschwindigkeit reduziert (Dehnung) oder erhöht (Stauchung). Hierbei ändert sich natürlich auch die Frequenz des Samples.
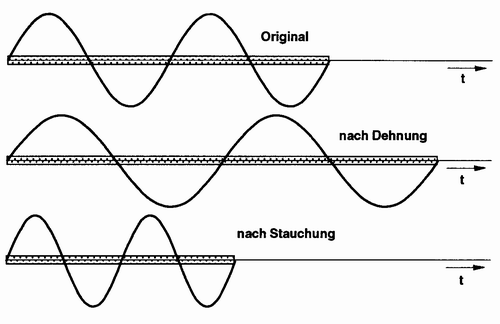
Abbildung 33: Dateidehnung und -stauchung und die damit verbundene Änderung der Abspielgeschwindigkeit
Beim Pitching wird nur die Tonlage verändert und anders als bei der Veränderung der Abspielgeschwindigkeit nicht die Abspielzeit. Das erreicht man, indem man das Audiomaterial um ein bestimmtes, wählbares Intervall verschiebt (transponiert). Man kann so also zum Beispiel die Tonlage um eine Quinte erhöhen, ohne die Abspielzeit zu beeinflussen.
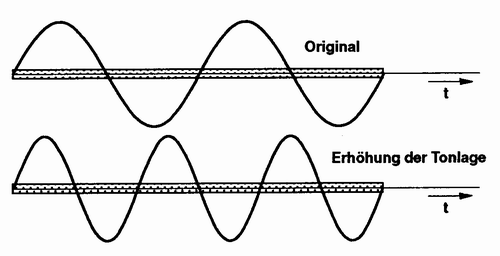
Abbildung 34: Tonlagentransponierung um den Faktor 1,5
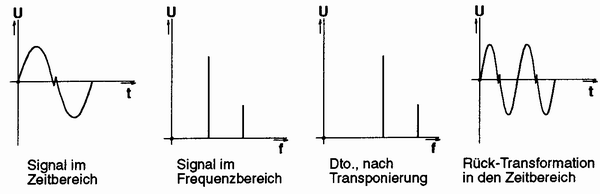
Abbildung 35: Vorgänge bei der Tonlagen Transponierung
Beim Timestretching wird die Länge des Audiomaterials verändert, die Tonhöhe bleibt dabei unverändert. Die Klangqualität nimmt mit steigernder Größe des Intervalls bzw. der Zeitabweichung Systembedingt ab. Aufwendigere Algorithmen versuchen die Formanten des Audiomaterials zu rekonstruieren, um den Qualitätsverlust zu minimieren.
Das kann hier nur ein Ausschnitt bleiben und ich hätte sicherlich noch eine Menge sagen bzw. schreiben können, aber damit sollten wir uns begnügen.
Quellen: