Dieses Kapitel gibt eine Übersicht zur Verwendung und Definition von Typen in Haskell. Das Grundsystem von Haskell bietet schon eine Reihe von vordefinierten Typen, wie zum Beispiel 'Int' für ganze Zahlen, 'Float' für reele Zahlen, oder 'Char' für alphanumerische Zeichen. Dieses Kapitel zeigt, wie die schon vorhandenen Typen um eigen Definierte ergänzt werden können.
2.1. TypsignaturFunktionen werden anhand einer Typsignatur beschrieben. Diese Signaturen sind zwar nicht nötig, erhöhen aber das Verständnis beim Lesen des Quelltextes. Die Signatur beinhaltet diejenigen Typen, die in der zu beschreibenden Funktion als Parameter und als Ergebnis vorkommen. Die einzelnen Typen werden in der Signatur durch Pfeile getrennt. Der äußerst rechts stehende Typ gibt dabei den Ergebnistyp an, alle links von diesen die Typen der Parameter der Funktion.
inc :: Int -> Int
Diese Typsignatur definiert eine Funktion mit dem Namen inc, welche als Parameter einen Wert vom Typ Int verlangt und als Ergebnis einen Wert von Typ Int zurückliefert. Die Pfeilnotation läßt sich als ein "...wird abgebildet auf..." lesen, also in diesem Beispiel: "Ein Int wird abgebildet auf ein Int ". Ein passender Ausdruck zu dieser Signatur ist folgender:
inc x = x + 1
Die formalen Parameter einer Funktion werden in Haskell, jeweils durch
ein Leerzeichen getrennt, dem Funktionsnamen nachgestellt.
Dabei ist die Reihenfolge einzuhalten, wie sie in der Typsignatur
vorgegeben wurde.
Ähnlich ließe sich die Zahl Pi
definieren, allerdings ohne Paramter:
pi :: Float
pi = 3.14159
Wird der Funktionsname in Klammern gesetzt, so handelt es sich um einen
Infix-Operator. Bei Infix-Operatoren müssen, wenn sie
aufgerufen werden, die Parameter nicht hinter dem Funktionsnamen
stehen, sondern der erste Parameter wird vor den Funktionsnamen,
der zweite hinter den Funktionsnamen geschrieben.
Hier ein Beispiel mit dem Plusoperator:
(+) :: Int -> Int -> Int
Aufgerufen wird diese Funktion nicht
+ 5 6
, sondern
5 + 6
Da es dem Programmierer sicherlich nicht ausreicht, stets mit den vorhandenen Typen zu arbeiten, bietet Haskell die öglichkeit eigene Typen zu definieren. Dies geschieht mit Hilfe der data-Deklaration. Diese teilt sich auf in einen Typ-Konstruktor und in einen oder mehrere Datenkonstruktoren. Der Typ-Konstruktor stellt den Bezeichner des erzeugten Datentyps dar. Der Daten-Konstruktor stellt einen Wert des erzeugten Datentyps dar.
data Colors = Blue | Cyan | Yellow | Orange | Green
In diesem Beispiel eines Aufzählungstypen ist Colors der Typ-Konstruktor und die Farben Blue, Cyan, Yellow, Orange und Green die Daten-Konstruktoren. Wichtig ist, dass die Bezeichner der Typ-und Daten-Konstruktoren mit einem Großbuchstaben beginnen.
Die jeweiligen Daten-Konstruktoren lassen sich noch um Typvariablen erweitern.
data Point = Pt Int Int
Dieses Beispiel stellt einen Produkttyp dar. Der Daten-Konstruktor Pt wurde hier um zwei Typvaribalen vom Typ Int erweitert. Etwas Vergleichbares ließe sich in anderen Programmiersprachen mit "Records" realisieren.
Die Definitionsweise eines Aufzählungstyps lässt sich mit der eines Produkttyps
kombinieren, sodass sich ein Typ kreieren lässt, welcher
meherere Daten-Konstruktoren mit jeweils verschieden vielen
Typvariablen beinhaltet. Auch kann eine Typvariable eines Daten-Konstruktors
von jenem Typ sein, welcher gerade definiert wird, sodass sich
rekursive Datenstrukturen aufbauen lassen. Ähnlich sind auch wechselseitige
Rekursionen möglich, in denen sich mindestens 2 verschiedene Datentypen
gegenseitig verweisen.
Hier ist ein Beispiel eines rekursiven Datentyps,
der einen binären Baum darstellt:
data Tree = Leaf Int | Branch Tree Tree
aTree :: Tree
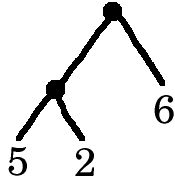
aTree = Branch (Branch (Leaf 5) (Leaf 2)) (Leaf 6)
ATree stellt einen Baum dar, welcher 2 miteinander verknüpfte Verzweigungen und 3 Blätter mit jeweils einem Zahlwert beinhaltet. ATree sieht graphisch folgendermaßen aus:
Weiter oben wurde schon der Datentyp Point mit dem Daten-Konstruktor Pt definiert. Der Typ ist für das Typsystem so zwar ausreichend definiert, aber ein Leser des Quelltextes weiß nur, dass die beiden Typvariablen des Daten-Konstruktors Zahlen beinhalten. Er weiß aber nicht, was diese Zahlen bedeuten. Hier wäre es schön, wenn die Typvariablen einen sprechenden Namen hätten. Abhilfe schafft hier das Verwenden von Feldbezeichnern.
data Point = Pt {pointx,pointy :: Int}
pointx und pointy sind in diesem Fall die Feldbezeichner. Haskell erzeugt aus diesen automatisch Zugriffsfunktionen, mit deren Hilfe die gewünschten Werte aus dem Datentyp auslesen lassen. Die Zugriffsfunktionen haben folgende Signatur:
Dies zeigt auch, dass die Feldbezeichner innerhalb einer data-Deklaration doppelt auftreten dürfen, allerdings zwischen verschiedenen data-Deklarationen nicht, da dort die Signatur der Zugriffsfunktion mit ihrem eindeutigen Namen nicht erstellt werden kann.pointx :: Point -> Int
pointy :: Point -> Int
absPoint :: Point -> Int
absPoint p = sqrt(pointx p * pointx p + pointy p * pointy p)
aPoint :: Point
aPoint = Pt {pointx = 1, pointy = 4}
Mit einer Update-Funktion lassen sich einzelne Typvariablen aktualisieren. Die Variable selbst wird dabei kopiert und der zu aktualiserende Wert durch den neuen ersetzt. Die restlichen Werte anderer Typvariablen werden unverändert übernommen.
aPoint2 :: Point
aPoint2 = aPoint {pointy = 5}
Hier tut sich ein Problem auf. Falls ein Datentyp mit mehreren Datenkonstruktoren
verwendet wird, kann es sein, dass der falsche Feldbezeichner zwar
auf einen richtigen Datentyp, aber auf einem falschen Daten-Konstruktor
angewendet wird. In diesem Fall kommt es zu einem Laufzeitfehler.
data PointDim = Pt2d {pointx,pointy :: Int} | Pt3d {pointx,pointy,pointz :: Int}
myPoint :: PointDim
myPoint = Pt2d {pointx = 1, pointy = 3}
myPoint2 :: PointDim
myPoint2 = myPoint {pointz = 5} --myPoint hat Pt2d als Wert, welcher 'pointz' nicht kennt --> Laufzeitfehler!!!
Das Definieren von Datentypen mit der data-Deklaration wird im
Zusammenhang mit der Polymorphie noch einmal angesprochen.
Stets nur mit Typbezeichern wie Int oder Float zu arbeiten, kann bei großen Programmen unübersichtlich werden. Genauso statt eines Strings, den es als Grundtyp in Haskell nicht gibt, ständig [Char] zu schreiben, ist nicht sehr schön und übersichtlich. Hierfür gibt es Typsynonyme, welche keinen neuen Typ erzeugen, sondern nur einem vorhandenen Typ einen Alias geben.
type String = [Char]
Genauso ließe sich der oben definierte Typ "Point" so darstellen:
type pointx = Int
type pointy = Int
data Point = Pt pointx pointy