Der Algorithmus von Edmonds für Matching in allgemeinen Graphen
John Freytag
Matching (Paarung) auf einem Graph
Graph G = (V, E) mit Knoten V und Kanten E
Pfad p auf einem Graph als Folge von Knoten:
p = [u1, u2, ..., uk]
Matching: Menge an Kanten, bei denen kein Knoten mehr als einmal vorkommt
Matching-Problem: Finde maximales Matching M mit größter Kardinalität |M| in G
Vokabeln
Kanten, die in M sind, heißen matched (gepaart)
Kanten außerhalb von M sind frei
Knoten, die zu keiner matched Kante gehören, sind freiliegend
Pfad p ist alternierend, wenn seine Kanten abwechselnd in M und nicht in M sind
beginnt und endet alternierender Pfad p auf freiliegenden Knoten, ist er erweiternd
Warum ist das wichtig?
Wenn P die Menge der Kanten auf erweiterndem Pfad p für Matching M ist,
dann ist M' = M Δ P ein Matching mit der Kardinalität |M| + 1
M
M '
M Δ P = (M - P) ∪ (P - M) symmetrische Differenz
Ein Matching auf einem Graph G ist (nur dann) maximal, wenn es in G keinen erweiternden Pfad für M gibt.
Lösung für bipartite Graphen
Vorgehen also:
- Zu gegebenem Matching M erweitertenden Pfad p suchen
- Wenn p gefunden, dann M mit p erweitern und zurück zu 1.
- Wenn kein p gefunden, dann ist M maximal
Für bipartite Graphen B=(V,U,E) (zwei Partitionen von Knoten, keine Kanten innerhalb von Partitionen) ist das einfach zu lösen:
Jeder erweiternde Pfad muss in V anfangen und in U aufhören, bzw. umgekehrt.
Wir können daher an jedem freiliegenden Knoten in V eine Breitensuche durchführen,
bei der wir zwischen freien und matched Kanten alternieren, bis wir einen freiliegenden Knoten in U gefunden haben oder nicht weiterkommen.
Lösung für bipartite Graphen
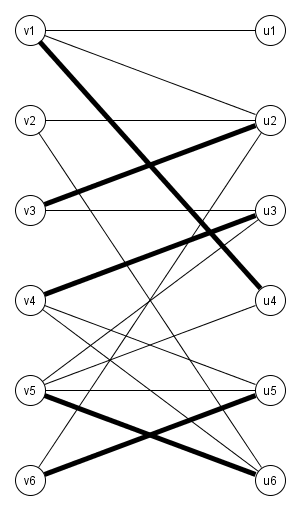
Lösung für bipartite Graphen
Neue Vokabel: Ist (u,v) eine matched Kante, dann ist v der Partner von u
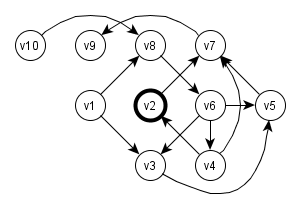
Es fällt ein Muster auf: Jedes Mal, wenn wir bei der Suche auf der rechten Seite (U) sind, ist der nächste Schritt automatisch der Partner des aktuellen Knotens in V
Wir können den Graphen also zu einem gerichteten Hilfsgraphen (V, A) reduzieren, bei dem die Kanten (vi, vk) nur dann in A sind, wenn vi mit dem Partner von vk verbunden ist
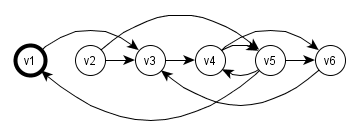
Ein Algorithmus mit diesem Vorgehen löst das Matching-Problem für bipartite Graphen B=(V,U,E) in O(min(|V|, |U| · |E|)
Allgemeine Graphen: Blüten
Der einzige Unterschied von bipartiten Graphen zu allgemeinen Graphen: bipartite Graphen haben keine Zirkel mit ungerader Kantenanzahl
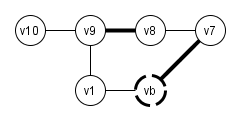
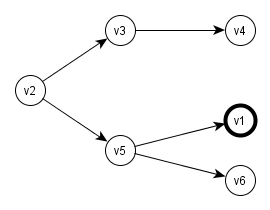
Versuchen wir unseren Ansatz bei Graphen mit solchen Zirkeln, schlägt der Algorithmus fehl:
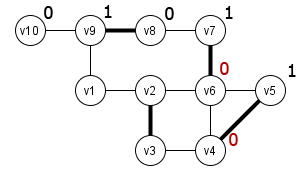
Laut Hilfsgraph rechts ist die Folge q' = (v1, v8, v6, v5, v7, v9) eine gültige Lösung
Der daraus entstehende "Pfad" q = [v1, v9, v8, v7, v6, v7, v8, v9, v10] ist aber ungültig! Knoten kommen doppelt vor und die Folge ist nicht mal alternierend!
Allgemeine Graphen: Blüten
Es zeigt sich, dass der Algorithmus fehlschlägt, wenn ungerade Zirkel mit dichter Anzahl an matched Kanten vorkommen (k matched Kanten auf 2k+1 Knoten)
Diese Zirkel heißen Blüten und sind leicht während der Pfadsuche zu erkennen, wenn wir unsere Knoten wie folgt markieren:
Knoten auf dem Pfad, die einen geraden Abstand zum Startknoten haben, sind "außen" (0)
Knoten mit ungeraden Abstand sind "innen" (1)
Folgen zwei äußere Knoten aufeinander, haben wir eine Blüte
Allgemeine Graphen: Blüten
Umgang mit Blüte b: Schrumpfen - Ersetzen der gesamten Blüte mit einem einzigen Pseudoknoten
Aus Graph G wird dadurch G/b = (V/b, E/b)
V/b ist V ohne alle Knoten in b und einem neuen Knoten vb als Ersatz für b
E/b ist E ohne alle Kanten mit beiden Endpunkten in b und allen Kanten (v, u) bei denen u in b, aber v nicht in b, geändert zu (v, vb)

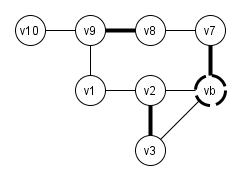
Dürfen wir das?
Wenn wir Blüten schrumpfen, dann müssen wir sicherstellen, dass dadurch keine erweiternden Pfade verloren gehen oder dazu kommen
Das ist nicht der Fall, denn es gilt:
Wenn wir bei der Suche nach erweiternden Pfaden ausgehend vom Knoten u eine Blüte b finden, dann
gibt es zu jedem Knoten in b einen alternierenden Pfad, der mit einer matched Kante endet.
Keine erweiternden Pfade gehen verloren.
Wenn wir bei der Suche nach erweiternden Pfaden ausgehend vom Knoten u in G eine Blüte b finden, dann gibt es in G für M einen
erweiternden Pfad von u aus, wenn es einen in G/b für M/b gibt.
Keine erweiternden Pfade kommen hinzu.
Allgemeine Graphen: Blüten
Erweiternden Pfad p gefunden. Wie kriegen wir aus vb jetzt den Teilpfad in der Blüte b im Originalgraphen?
- Wähle Nachfolger vk von vb in p
- Finde Knoten in b anliegend an vk
- Finde Pfad von Basis (Anfang) von b bis vk, der mit matched Kante endet
- Ersetze vb in p mit so gefundenem Pfad
Der Algorithmus von Edmons
für alle freiliegenden v in V:
Suche nach alternierenden Pfaden, die bei v starten
Schrumpfe alle gefundenen Blüten
wenn Pfad p auf freiliegendem Knoten endet:
p ist ein erweiternder Pfad
löse Blüten geschrumpfte Blüten auf
erweitere aktuelles Matching M mit p, beginne von vorne
sonst:
wenn kein erweiternder Pfad gefunden:
ignoriere v in weiteren Suchen
aktuelles Matching M ist maximal
(keine weiteren erweiternden Pfade)
Komplexität: O(|V|4)
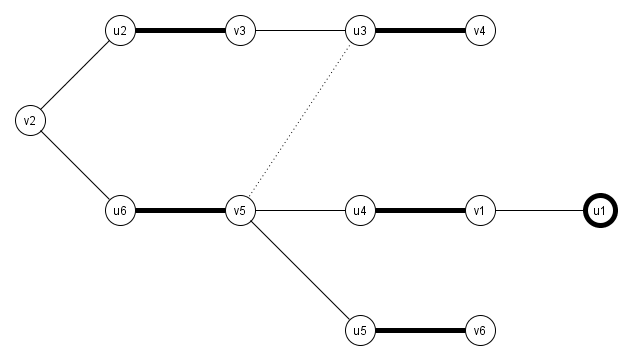
Beispiel
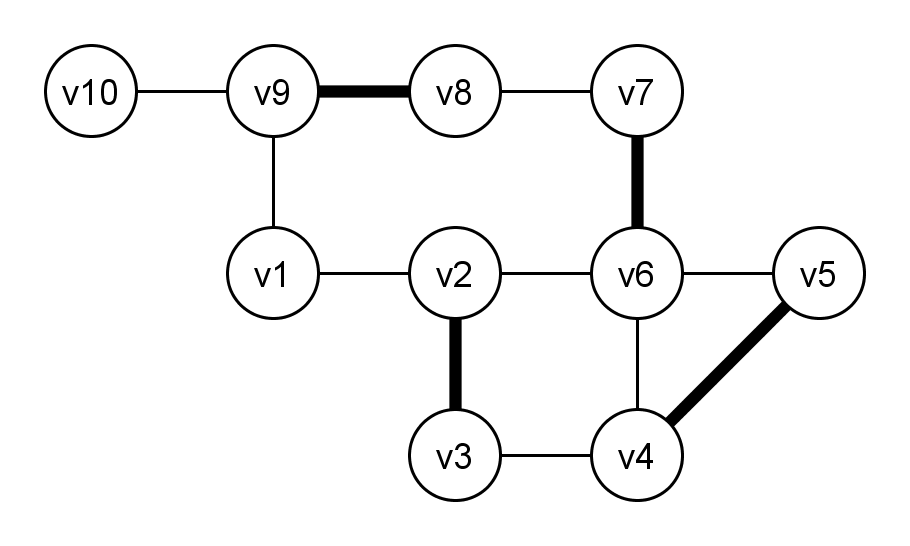
Die ersten Schritte sind trivial und werden hier daher übersprungen.
Beispiel
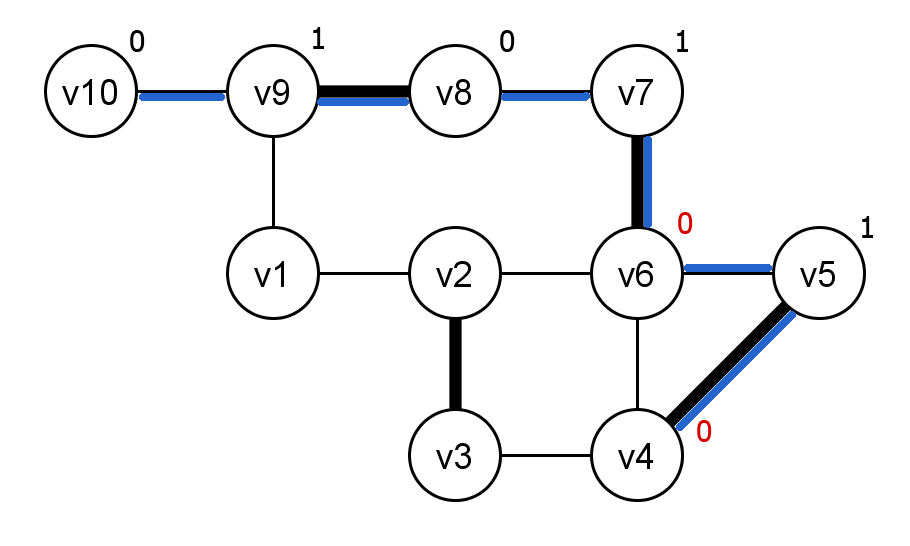
Beim Suchen des Pfades, ausgehend von v10, treffen wir auf eine Blüte
Beispiel
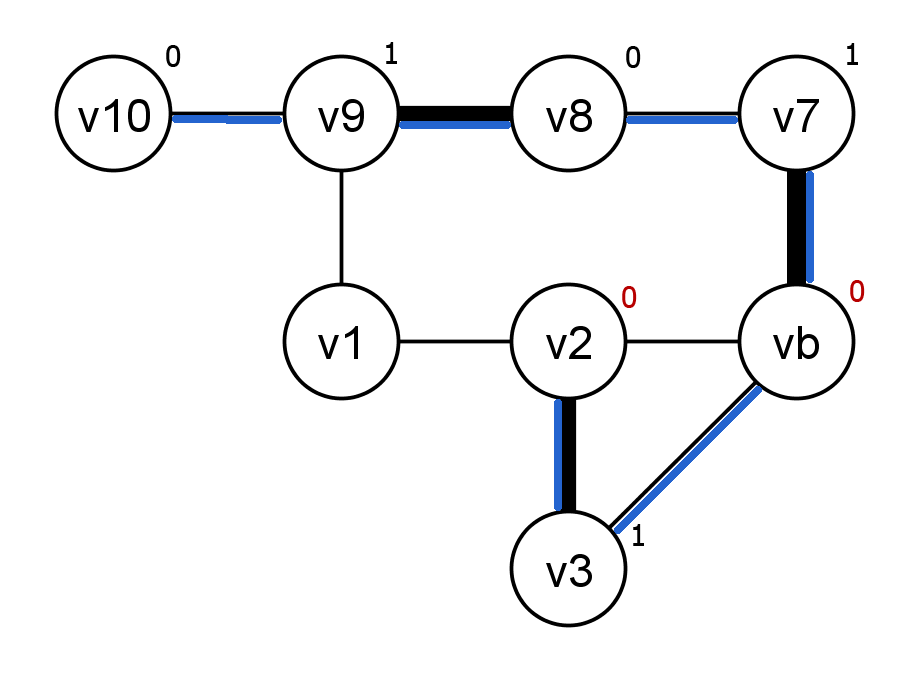
Nach dem Schrumpfen der ersten Blüte finden wir direkt die nächste
Beispiel
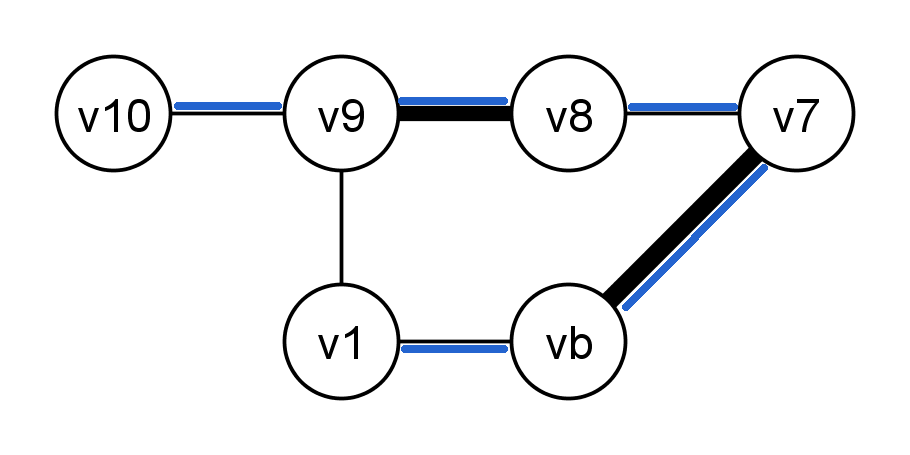
Jetzt, da beide Blüten geschrumpft sind, können wir den Pfad vollenden
Beispiel
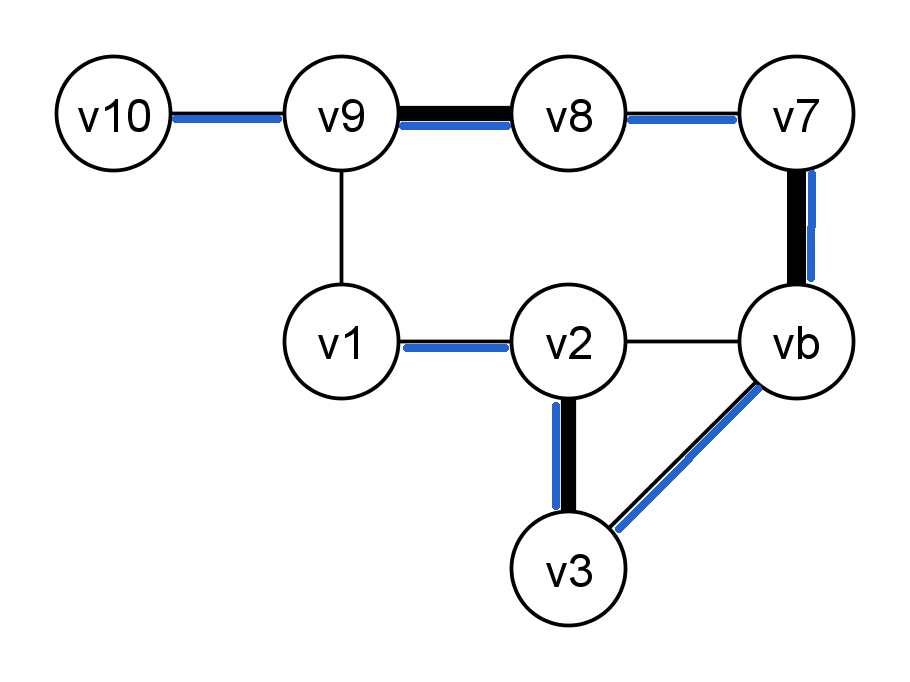
"Entschrumpfen" der ersten Blüte
Beispiel
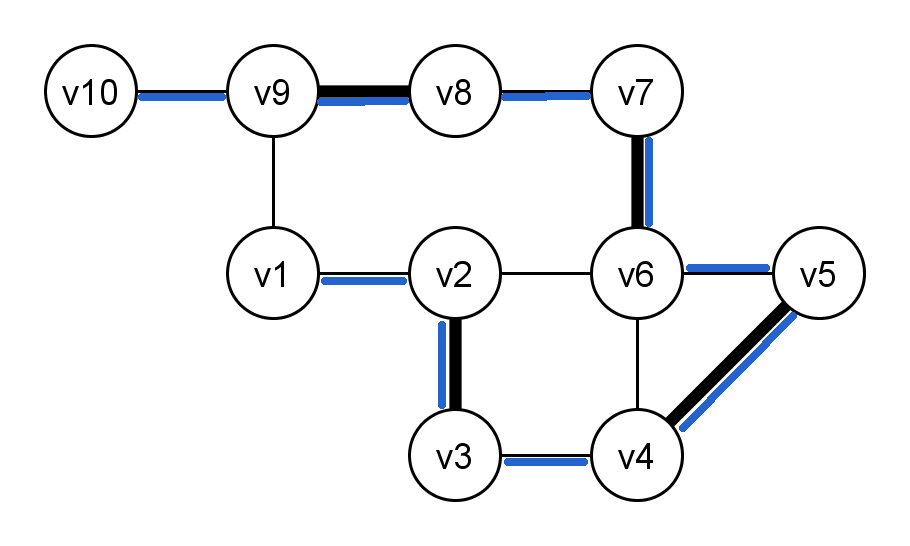
"Entschrumpfen" der zweiten Blüte - der Pfad ist komplett
Beispiel
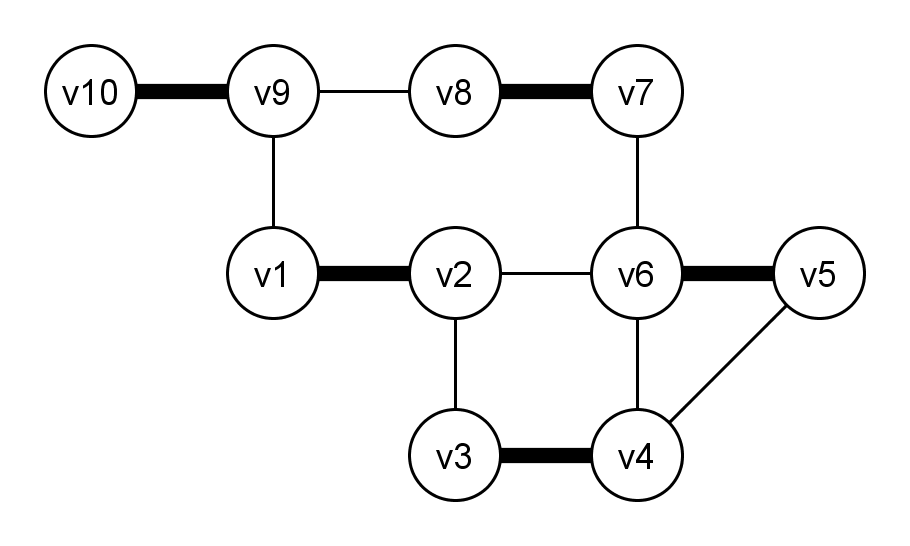
symmetrische Differenz der Pfad-Kanten mit unserem jetzigen Matching M gibt uns das neue (und maximale)