Transitive Hülle

1 Definition

Die transitive Hülle t(R) einer zweistelligen Relation R auf V ist die kleinste transitive Relation, die R enthält.

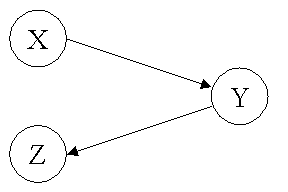
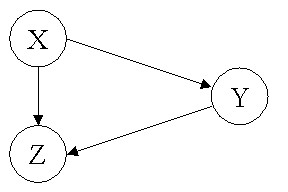
Faßt man R nun als Graphen auf V auf, wobei R die Menge aller Kanten und V die Menge aller Knoten sind, dann gibt es einen Weg von x nach z, genau dann, wenn es in t(R) eine Kante von x nach z gibt. Man kann also die Frage, ob es in einem Graphen einen Weg von x nach y gibt, direkt aus der transitiven Hülle ableiten.
 

Ein Graph...	...und seine transitive Hülle.

2 Eine mögliche Implementation

Diese Implementation basiert wieder auf diesen Definitionen:

procedure TGraph.TransHull;
var       y, x, i              :IndexType;
          KnotenX, KnotenY     :PKnoten;
          NewKante             :TKanteAdd;
begin
 ZeroKantenMarken;
 if FCount > 0 then        //sind Knoten vorhanden
  for y := 1 to FCount do
   begin
    KnotenY := PointItem(y);
    for x := 1 to FCount do
     begin
      KnotenX := PointItem(x);
      i := 0;
      while (i < KnotenX.KantenCount) and   //Schleife gibt den Index der Kante zurück,
            not (KnotenX.Kanten[i].DestKnoten = y) do  //die auf y zeigt (wenn es sie gibt).
       inc(i);
      if i < KnotenX.KantenCount then    // es gibt eine Verbindung
       begin                             // von x nach y
        i := 0;
        while i < KnotenY.KantenCount do // für jede Verbindung
         begin                           // von y nach z
          NewKante.SourceKnoten := x;    // es existieren Kanten von x nach y und y nach z...
          NewKante.DestKnoten := KnotenY.Kanten[i].DestKnoten;
          NewKante.Value := KnotenX.Value + KnotenY.Value;
          AddKante(NewKante);            // ...und damit auch von x nach z
          inc(KnotenX.Kanten[KnotenX.KantenCount - 1].Marke);
          inc(i);
         end; // while i < KnotenY.KantenCount
       end; // if i < KnotenX.KantenCount
     end; // for x := 1 to FCount
   end; // if FCount > 0; for y := 1 to FCount
end;

 zurück zur Startseite