(1) Definition und Beispiele

Ein Graph ist ein Modell zur Beschreibung von Objekten, die untereinander in gewisser Beziehung stehen. Die Objekte werden als Knoten, die Beziehungen als Kanten (Verbindungslinien zwischen den Knoten) dargestellt. Knoten haben Namen und können Träger von Werten, Eigenschaften, etc. sein.

Mathematisch ist ein Graph G eine beliebige Teilmenge der Produktmenge V x V mit V = beliebige Menge von Knoten. Ein Graph ist daher irgendeine Menge von Paaren der Form  ( x, y ) mit x  V und y  V.


 

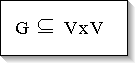
Beispiele:

V1 = Menge aller Flughäfen in Deutschland
G1 = { ( x, y )  V1 x V1 | Es gibt einen Direktflug von x nach y }

V2 = Menge aller IA´s im 5. Semester
G2 = { ( x, y )  V2 x V2 | x macht die OOP-Übungen zusammen mit y }
 
 
 
 

Darstellung:

Knoten  V

Kanten  ( x, y )  G
 
 

 

Beispiel für einen Graphen:
 

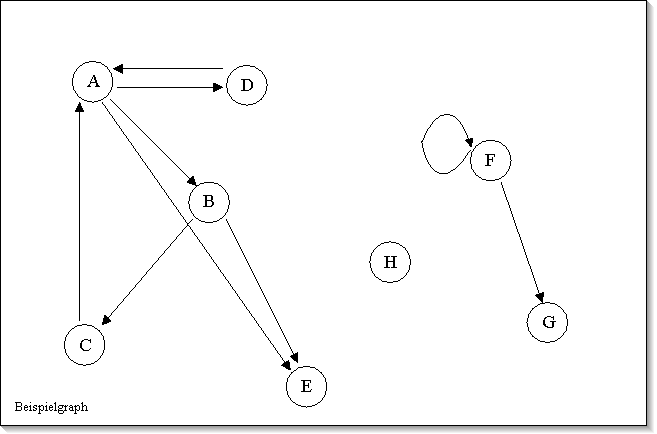
V1 = { A,B,C,D,E,F,G,H }
G1 = { ( A, D ), ( D, A ), ( A, B ), ( B, C ), ( C, A ), ( B, E ), ( A, E ), ( F, G ), ( F, F ) }

weitere Beispiele
 
 

Typen:

Graphen, die zu jedem Pfeil von x nach y auch einen Pfeil von y nach x besitzen, heißen ungerichtete oder symmetrische Graphen. Statt der beiden gerichteten Kanten ( Pfeile ) zeichnet man dann einfach eine ungerichtete Kante.
 


 

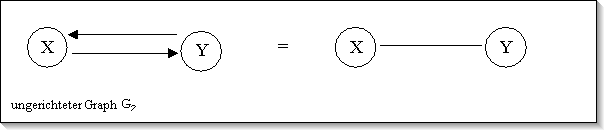
Im Gegensatz zu den gerichteten Graphen wird für die Elemente ungerichteter Graphen keine Ordnung verlangt. Die ungerichtete Kante von x nach y notiert man durch { x, y }, den ungerichteten Graphen durch G2 = { { x, y } }.
 
 
 

Graphen bei denen jeder Kante ein Wert zugeordnet ist, nennt man gewichtete oder bewertete Graphen. Dieser Kantenwert kann reell oder ganzzahlig sein.


 
 


 


 

(2) Wege und Zusammenhang

In einem Graphen ist ein Weg ( oder Pfad ) von x nach y mit der Länge n eine Folge x = K1, K2, ..., Kn = y von Knoten, in der es jeweils Kanten von K1 nach K2, von K2 nach K3 usw. bis nach Kn gibt. Ein Weg ergibt sich also aus aneinandergehängten benachbarten Kanten, seine Länge aus der Anzahl der enthaltenen Knoten. Kommt auf einem Weg kein Knoten doppelt vor, so ist er einfach. Ein einfacher Weg von x nach x ist ein Zyklus.

Beispiele für Wege

 

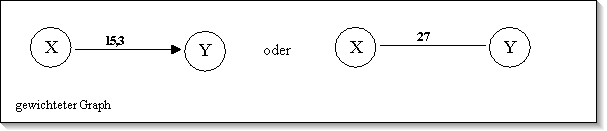
Ein Graph, bei dem es zwischen je zwei ( verschiedenen ) Knoten einen Weg gibt, heißt zusammenhängender Graph. Ein nicht zusammenhängender Graph wird aus einer Vereinigung zusammenhängender Komponenten gebildet. Ein zusammenhängender und zyklenfreier Graph ist ein Baum.
 ( Eine Gruppe nicht zusammenhängender Bäume ist ein Wald. )
 
 

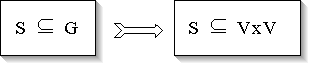
Jeder zusammenhängende Graph G besitzt einen erzeugenden Baum, auch Spannbaum genannt. Der Spannbaum S ist ein zyklenfreier, zusammenhängender Teilgraph von G. Daraus folgt, daß S auch Teilmenge von V x V ist.
 


 

Beispiele für Spannbäume

Bei den meisten Graphen gibt es mehrere Möglichkeiten einen erzeugenden Baum zu konstruieren. Die Regel dafür lautet:


 

Warum ist der Spannbaum interessant?
 Stellt man z.B. ein Rechnernetz als gewichteten Graphen dar, könnte der Kantenwert die Kosten einer Leitung (Kante) zwischen Rechnern (Knoten) angeben. Will man nun die niedrigsten Kosten für das Netz in Erfahrung bringen, so sucht man den Spannbaum, bei dem die Summe der Kosten seiner Kanten am geringsten ist (minimaler Spannbaum).
 

Bei nicht zusammenhängenden Graphen wird für jede Komponente ein Spannbaum gebildet. Alle Spannbäume zusammen bilden dann einen spannenden Wald.

Beispiel für spannenden Wald
 
 


 


 

(3) Repräsentation

Die Kantenbeziehungen eines Graphen ( d.h. eine Teilmenge von V x V ) können wir durch eine boolesche Matrix, die Adjazenzmatrix darstellen.

boolean [] [] Graph ;

Voraussetzung ist dabei, daß die Knoten ( die Elemente von V ) irgendwie fortlaufend bezeichnet werden ( V also eine Aufzählung der Knoten ist ). Bei n Knoten wird die n x n - Adjazenzmatrix definiert durch:

A( i, j ) =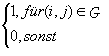 
 

Die Adjazenzmatrix für einen ungerichteten Graphen ist immer symmetrisch, d.h.: A( i, j ) = A( j, i ) für alle i, j  V

Beispiel für Adjazenzmatrix
 
 

Eine andere Möglichkeit einen Graphen darzustellen ist die Adjazenzliste. Dabei wird für jeden Knoten eine Liste definiert, in der die Adjazenz - knoten ( unmittelbare Nachbarn ) enthalten sind.

Beispiel für Adjazenzliste
 
 

Liste oder Matrix ?

Die Darstellung als Liste vermeidet die speicheraufwendige ( und hochgradig redundante ) Adjazenzmatrix und spart somit Speicherplatz. Dafür ist der Aufwand für einen Zugriff auf den Wert einer Kante bei der Listendarstellung hoch, während bei Verwendung der Matrix der Zugriff direkt möglich ist.
 
 


 


 

Anwendung:

Viele klassische Beispiele für Graphen kommen aus dem Bereich der Verkehrsnetze. Deshalb haben wir zur Erläuterung der folgenden Algorithmen ein Beispiel aus diesem Bereich gewählt.

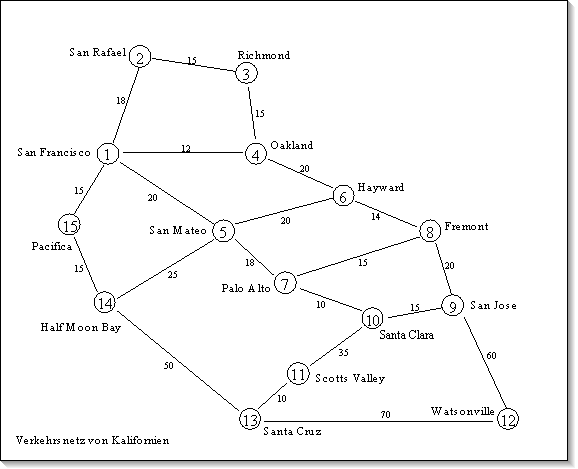
Wir haben eine Menge von Städten rund um die Bucht von San Francisco. Die Kanten repräsentieren mögliche direkte Verkehrsverbindungen (Straßen) zwischen den Städten. Sie sind mit einer Maßzahl bewertet, die für die Entfernung und/oder den durchschnittlichen Zeitaufwand für eine Fahrt zwischen den Städten steht. Jeder Knoten hat einen Stadtnamen und eine Nummer in der Aufzählung.
 
 

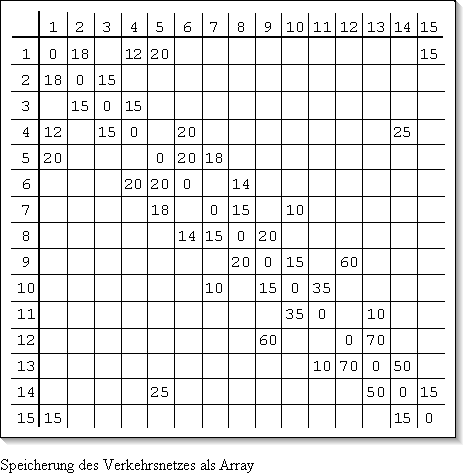
Bei dieser Matrix sind die Einträge keine booleschen Werte mehr, sondern entsprechen den Bewertungen der Kanten. Kein Wert ( - ) in der Matrix bedeutet, es gibt keine direkte Verbindung zwischen den Städten. Die Nullen in der Diagonalen sind die Bewertung jeder Stadt mit sich selbst.
 
 

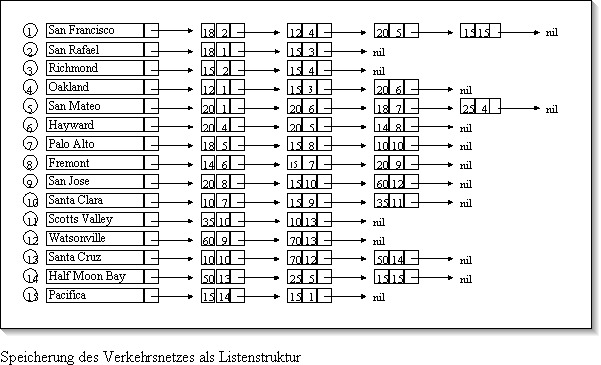
Bei diesen Listen ist zu jedem Nachbarknoten außer der Nummer auch der Wert der Kante, die ihn mit dem Anfangsknoten verbindet, in einer Infokomponente gespeichert.