| Herstellen
der Heapeigenschaft
Jeder Knoteninhalt wird mit seinem direkten Vorgänger im Heap
verglichen.
Ist er kleiner als mindestens einer seiner Nachfolger, so wird der
kleinere mit dem größeren vertauscht.
Nach jedem Absenkvorgang wird der darüberliegende Teil des
Baumes nochmals überprüft.
Ein Element kann vor bzw. während der Herstellung der Heap-Eigenschaft
die Wurzel des Baumes sein, sich nach dem vollständigen Absenkvorgang
aber durchaus in der untersten Ebene befinden.
Weitere Informationen 
Zwei
unterschiedliche Einfügeverfahren
Das Bottom-Up-Verfahren:
Die zu sortierenden Elemente, werden bei diesem Verfahren
Stück für Stück in den Heap eingetragen. Und zwar in der
Reihenfolge ihres Auftretens. Das erste Element wird also in unserem Heap
zur Wurzel. Die Elemente zwei und drei werden dann als Nachfolger der Wurzel
angesehen. Die Elemente vier bis sieben werden zum Nachfolger der Nachfolger
der Wurzel, usw.

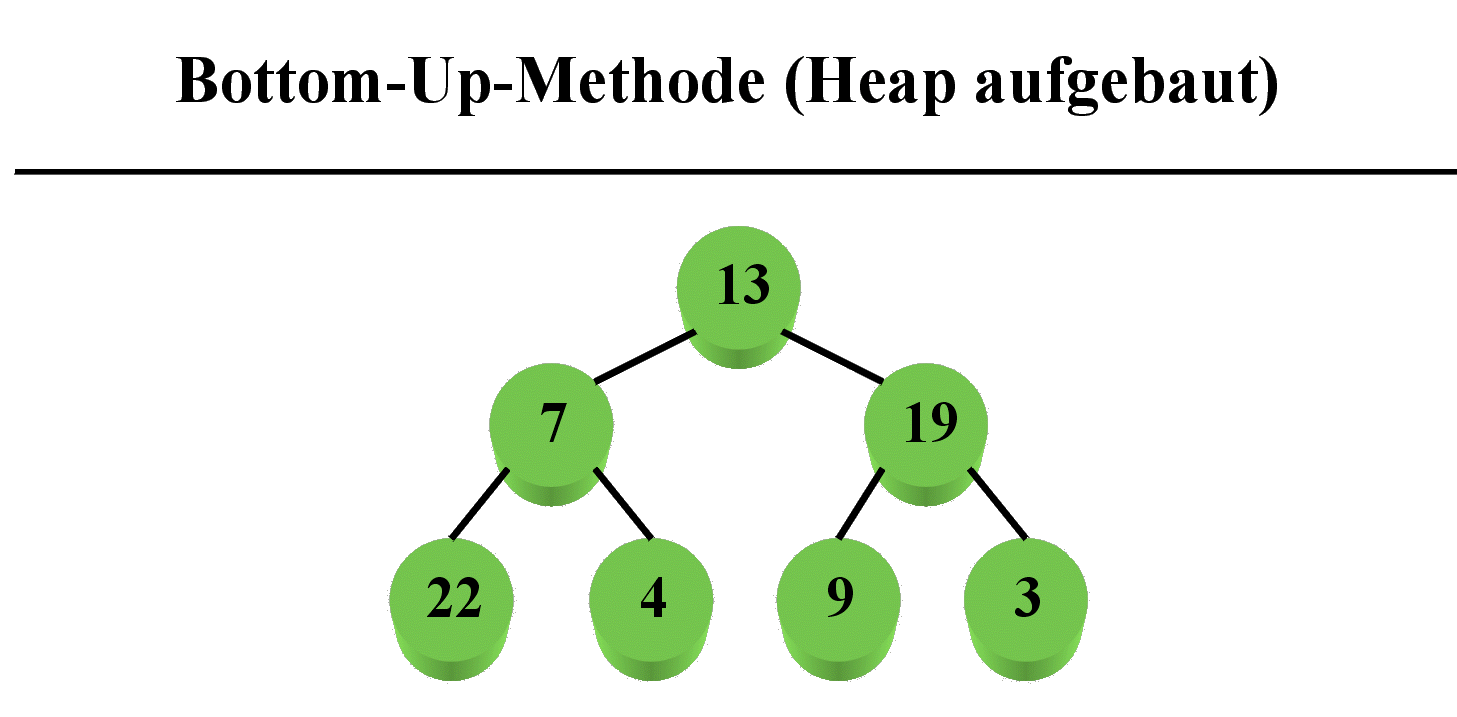
Ist der Einfügevorgang abgeschlossen, wird in einem
zweiten Schritt die Heap-Eigenschaft hergestellt.
Das Top-Down-Verfahren:
Genau wie beim Bottom-Up-Verfahren werden beim Top-Down-Verfahren
die Elemente schichtweise in einen Heap übernommen. Dies geschieht
wiederum in der Reihenfolge des Auftretens. Der Unterschied zum Botton-Up-Verfahren
besteht darin, dass beim Top-Down-Verfahren die Heap-Eigenschaft nach jedem
neu eingefügten Element wiederhergestellt wird. Es kann daher vorkommen,
daß ein neu eingefügtes Element von der untersten Ebene bis
zur Wurzel 'aufsteigt', da beim Top-Down-Verfahren von der Wurzel zur untersten
Ebene hin sortiert wird.

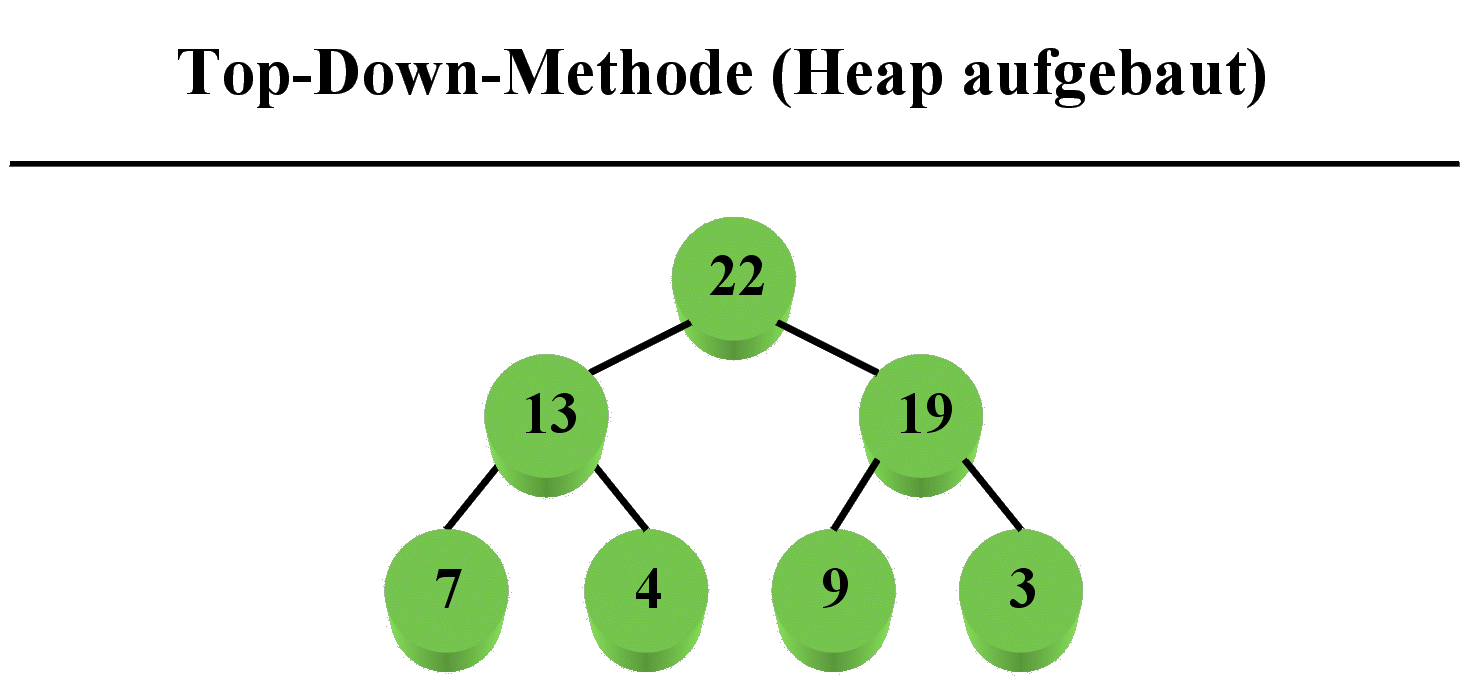
Unterschiede
& Gemeinsamkeiten
Vom Zeitaufwand her sind sich beide sehr ähnlich, das Top-Down-Verfahren
ist jedoch etwas langsamer.
Beide Verfahren benötigen die gleiche Zeit für die Eintragung
der Elemente in die Datenstruktur.
Das Top-Down-Verfahren benötigt aber mehr Sortierschritte,
da nach jedem neuen Element wieder die Heap-Eigenschaft hergestellt wird.
Die einzelnen Sortierschritte der beiden Verfahren sind gleich aufwendig:
Beide Algorithmen operieren entlang eines Pfades (path) von der Wurzel
zum unteren Ende des Heaps (oder andersherum, je nach Verfahren).
Größe des Heaps
Es gibt etwa n/2 Knoten auf der untersten
Ebene, n/4 Knoten mit direkten Nachfolgern
auf der untersten Ebene, n/8 Knoten mit zwei
Nachfolgern auf der untersten Ebene usw.
Jede Ebene besitzt zudem halb so viele Knoten wie die nächste,
woraus folgt, daß höchstens log(n) Ebenen existieren können.
Weitere Informationen 
Ablauf
(Modell)
Heap wird abgebildet auf einen binären
Baum:
-
Füge alle Elemente in einen "binären
Baum" ein.
-
Stelle die Heapeigenschaft her.
-
Bis der "Baum" leer ist,
-
entferne die Wurzel durch Ersetzung mit dem am
weitesten rechts stehenden Blatt der untersten Baumebene (höchster
Index).
-
stelle die Heapeigenschaft wieder her.
Ablauf
(real)
-
Ordne das Feld mit dem obigen Verfahren so um, daß die Heap-Bedingung
erfüllt ist.
-
Bis der Heap nur noch aus einem Element besteht,
-
Vertausche das erste Element mit dem letzten, so daß das größte
Feldelement auf der letzten Feldposition liegt.
-
Ordne das Feld so um, das die ersten Elemente (bis auf das letzte) die
Heap-Bedingung erfüllen. Dies entspricht einer Verkleinerung des Heaps
um eins.
Datenstruktur
Heapsort wird, wie zu Beginn erwähnt, nur innerhalb einer zugrunde
liegenden Datenstruktur ausgeführt. Die Element, müssen in eine
Feldstruktur, z.B. in ein Array geschrieben werden, es wird also kein
binärer Baum erzeugt! Die Elemente wurden nur innerhalb ihrer Datenstruktur
vertauscht, bis diese die Heap-Eigenschaft erfüllen.
Weitere Informationen 
Animiertes
Heapsort-Verfahren (70 Bilder, ca. 2:30Min.) (Start) (Start)
Einsatz
von Heapsort
Heaps sind hervorragend zur Implementierung von priorisierten Warteschlangen
geeignet.
Gewöhnlich werden Warteschlangen einfach durch lineare Listen
verwirklicht. Die Elemente, die eingefügt werden sollen, werden dann
nach ihrer Dringlichkeit in diese Liste einsortiert. In einer Schlange
der Größe n ist dabei für
jede Einfüge- bzw. Entfernenoperation der Aufwand linear. Die Effizienz
einer priorisierten Warteschlange läßt sich deutlich steigern,
wenn man sie in Form eines Heaps organisiert.
Für das Einfügen oder Entfernen eines Elements sind dann
nur maximal log(n) Schritte erforderlich.
Wenn man ein neues Element anfügen möchte, so setzt man
es einfach ans untere Ende des Heaps und läßt es solange aufsteigen,
bis die Heapeigenschaft wiederhergestellt ist.
Beim Entfernen eines Elements greift man einfach auf die Wurzel
des Heaps zu.
Weitere Informationen 

|