Die grundlegende Prozedur des Heapsort-Verfahrens ist die Prozedur downheap. Sie hat die Aufgabe das Element des Startknotens in dem Heap absinken zu lassen, wenn einer der beiden direkten Nachfolgeknoten größer ist. 
Dasselbe Verfahren wird daraufhin mit diesem Nachfolgerknoten durchgeführt. Spätestens bei einem Blatt endet das Verfahren, da alle Blätter die Heap-Eigenschaft haben. 
 

procedure downheap (var a : feld; k, n : integer);
{ k ist der Startknoten, n ist die Länge des Arrays }

var f      : integer; 
    isheap : boolean; begin
  isheap:=false;
  while (k <= n div 2) and not isheap do    { k ist kein Blatt }
  begin
    f:=2 * k;                                                 { erster Nachfolger }
    if f + 1 <= n then                                    { existiert zweiter Nachfolger? }
      if a[f+1] > a[f] then                              { f ist der Nachfolgerknoten 
                    f:=f + 1;                                     mit dem größeren Element }

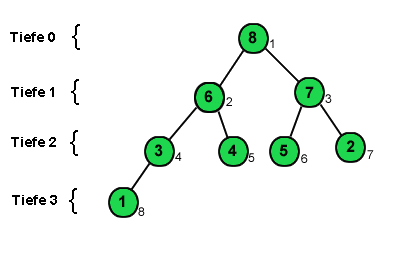
Die folgende Prozedur buildheap macht ein unsortiertes Array zu einem Array mit Heap-Eigenschaften, indem bottom-up alle Teilbäume mittels downheap zu Heaps gemacht werden. Statt bei den Blättern zu beginnen, die ja ohnehin bereits die Heap-Eigenschaft haben, genügt es auch, bei den Knoten der jeweiligen Blätter zu beginnen. 
 

procedure buildheap (var a : feld; n : integer);

var k : integer;
begin
  for k:=n div 2 downto 1 do downheap (a, k, n);
end;
 
 

Die Prozedur heapsort konstruiert zunächst mittels buildheap aus den zu sortierenden Elementen einen Heap.
Anschließend wird die Wurzel mit dem Blatt maximaler Tiefe durch exchange vertauscht und mit downheap die Heap-Struktur wiederhergestellt. Am Ende ist das Array in aufsteigender Reihenfolge sortiert. 
 

procedure heapsort (var a : feld; n : integer);

var k : integer;
begin
  buildheap(a, n);
  for k:=n downto 2 do
  begin
    exchange (a[1], a[k]);
    downheap (a, 1, k-1);
  end;
end;

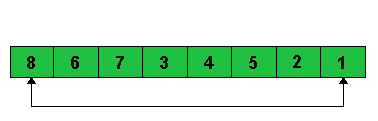
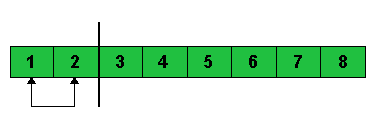
.	Erstes Element (das größte im Heap) wird mit dem letzten Element im Array getauscht.
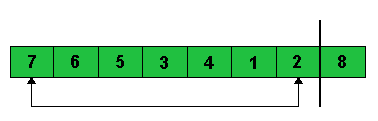
	Gesamtindex des Arrays wird dekrementiert, die Heapeigenschaft hergestellt und wieder  das erste Element mit dem letzten getauscht.
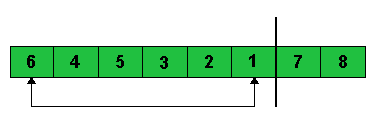
	Gesamtindex des Arrays wird wieder dekrementiert, die Heapeigenschaft hergestellt und wieder das erste Element mit dem letzten getauscht.
	...  und so weiter ...
	Nun wurden die letzten beiden Elemente getauscht und das Array ist aufsteigend sortiert.