Alle bisher behandelten Sortierverfahren wie Quicksort und Bubblesort benötigen im schlimmsten Fall (Worst-case) eine Laufzeit von (N²) für das Sortieren von N Schlüsseln. Wenn Informationen über die Ordnung der Schlüssel nur durch Schlüsselvergleiche gewonnen werden können, wird zum Sortieren von N Schlüsseln mindestens (N log N) Schritte benötigt.
Solche Sortierverfahren heißen allgemeine Sortierverfahren, weil außer der Existenz einer Ordnung keine speziellen Bedingungen an die Schlüssel geknüpft sind.

Def. "Schlüssel":
Als Schlüssel wird ein Datum bezeichnet, das meistens ganzzahlig (Kontonr., Matrikelnr.)
aber auch alphabetisch (lexikographisch) aufgebaut ist.
Zwischen den Schlüsseln besteht eine Ordnungsrelation (z.B."<="oder">=").

Das Sortieren mit einer Halde (Heap) folgt dem Prinzip des Sortierens durch Auswahl, wobei aber die Auswahl geschickt organisiert ist. Heapsort wurde 1964 von Williams und Floyd beschrieben. Es sortiert seine Objekte durch Auswahl. Mit einer worst - case Laufzeit von (N log N) ist er das am längsten bekannte, asymptotisch optimale allgemeine Sortierverfahren.
Er verwendet keinen zusätzlichen Speicherplatz. Leider ist seine innere Schleife ein gutes Stück länger als die innere Schleife von Quicksort, und sie ist im Durchschnitt ungefähr halb so schnell wie Quicksort.
Heapsort ist vorzugsweise dann einzusetzen, wenn viele Datensätze zu sortieren sind und die Sortierzeit vorhersagbar sein soll.
Die Idee besteht darin, einen Heap aufzubauen, der die zu sortierenden Elemente enthält, und sie danach alle in der richtigen Reihenfolge zu entfernen. Indem man Heapsort die Möglichkeit des direkten Zugriffs zum Feld gibt, wird die Berechnung so organisiert, daß das Sortieren an Ort und Stelle vorgenommen werden kann.
 

Der Heap (engl. = Haufen) ist eine Datenstruktur mit einer bestimmten Ordnungsrelation.
Eine Folge  F = k₁ ,k₂ , ... ,k_n  von Schlüsseln nennen wir einen Heap,  wenn:

Beispiel:
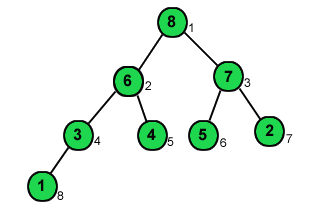
Die Folge  F = 8, 6, 7, 3, 4, 5, 2, 1  genügt der Heap-Bedingung, weil gilt:

8>=6,  8>=7,  6>=3,  6>=4,  7>=5,  7>=2,  3>=1

Diese Ordnungsrelation wird auch als Heap-Bedingung bezeichnet.

Wird die im Beispiel genannte Folge als Binärbaum interpretiert, so kann man die Heap-Bedingung auch wie folgt formulieren: ein Binärbaum ist ein Heap, wenn der Schlüssel jedes Knotens mindestens so groß ist wie die Schlüssel seiner beiden Nachfolger (falls es diese gibt).
In die oberste Zeile kommt der Schlüssel k₁, in die nächste Zeile kommen die Schlüssel  k₂ und  k₃.
Die Beziehungen  k₁ >= k₂  und  k₁ >= k₃  werden durch zwei Verbindungslinien (Kanten) dargestellt.
Die nächsten Schlüssel werden nach dem gleichen Prinzip von links nach rechts eingefügt.

Im Folgenden gehen wir davon aus, daß die Schlüssel in einem Array gespeichert sind, auch wenn wir in den weiteren Erklärungen auf die Baumstruktur Bezug nehmen. 
Wir nehmen an, daß die im obigen Beispiel genannte Folge ( F = 8, 6, 7, 3, 4, 5, 2, 1 ) als Heap gegeben sei, und die Schlüssel sollen in absteigender Reihenfolge ausgegeben werden.
 
 

Den ersten Schlüssel auszugeben ist ganz leicht, denn k₁  ist ja das Maximum aller Schlüssel.
Wie bestimmen wir aber jetzt den nächstkleineren Schlüssel?
Eine offensichtliche Methode ist doch die, den gerade ausgegebenen Schlüssel aus der Folge zu entfernen und die restliche Folge wieder zu einem Heap zu machen. Dann steht nämlich der nächstkleinere Schlüssel wieder an der Wurzel, und wir können nach demselben Verfahren fortfahren.

 

{Anfangs besteht der Heap aus Schlüsseln k₁ , ... , k_n }
Solange der Heap nicht leer ist, wiederhole:
      gib  k1  aus; {das ist der nächstgrößere Schlüssel}
      entferne  k1  aus dem Heap;
      stelle die Heap-Bedingung für die restlichen Schlüssel her,
            so daß die neue Wurzel an Position  1   steht.

Der schwierigste Teil der Methode ist das Wiederherstellen der Heap-Bedingung.
Eine detailierte Beschreibung, wie das funktioniert, folgt im nächsten Kapitel.
 

Heapsort ist ein schnelles (N log N), internes Sortierverfahren. Intern, weil es außer der zugrunde liegenden Datenstruktur (z.B. Feldstrukturen oder Arrays), in der die Schlüssel enthalten sind, keinen weiteren Speicherplatz benötigt. Dies liegt daran, daß die Schlüssel in der vorhandenen Datenstruktur nur verschoben werden, es müssen keine Elemente ausgelagert werden.

Zuerst wird ein Binärbaum nach der Heap-Bedingung mit den Schlüsseln der Folge gefüllt.
Es gibt zwei Arten den Heap zu erstellen. Das Bottom-Up-Verfahren und das Top-Down-Verfahren.

Bottom-Up-Verfahren

Beim Bottom-Up-Verfahren wird die Heap-Bedingung im Binärbaum von der untersten Ebene zur Wurzel durchgeführt.

Top-Down-Verfahren

Funktioniert wie das Bottom-Up-Verfahren, nur daß die Heap-Bedingung von der Wurzel zu der untersten Ebene hergestellt wird.
 

Eine detailierte Beschreibung der Einfügetechniken folgt ebenfalls später!